在MotionView前处理环境中，除了使用软件自带工具创建简单的模型外，还可以输入CAD创建复杂模型。在输入CAD模型时，零件的质量、转动惯量和质心位置信息可自动计算出来。同时，为方便边界条件的定义，MotionView可保留和应用CAD模型中的几何点信息。

本示例将练习以下4个方面内容：

●CATIA格式的装配体模型导入。

●根据多体动力学分析的需要进行模型简化。

●约束与其他控制参数定义。

●求解与结果查看。

练习开始前，复制chap03/CAD目录下的所有文件到工作文件夹，工作路径中不能含有中文字符。

STEP 01 CAD模型导入

本步将指导用户进行模型导入及简化。

（1）在MotionView中新建一个会话。

（2）在菜单栏中，选择File→Import→Geometry命令。此时，弹出Import CAD or FE对话框。

（3）在Import Option处，选择Import CAD or Finite Element Model With Mass and Inertias选项，即在输入模型的同时，计算模型各个零部件的质量及转动惯量信息。

（4）在Import File下拉列表中选择Catia。

（5）单击Import File栏的“文件浏览”按钮，选择工作文件夹下的Front Assembly.CATProduct。

（6）单击Open按钮。

（7）单击Output Graphic File栏的“文件浏览”按钮，指定输出文件为front_assembly.h3d。

（8）单击Save按钮。

（9）单击并展开MDL Options，可以观察到图3-1所示的选择面板。

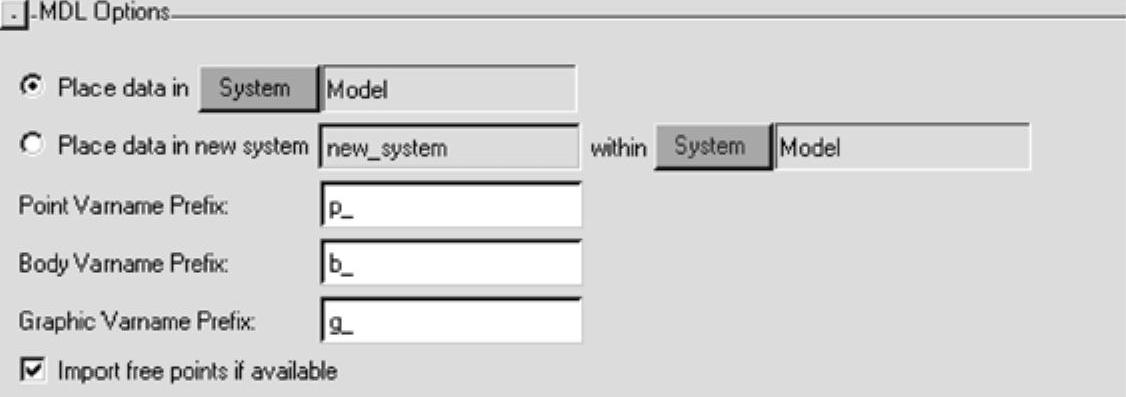
图3-1 Import CAD or FE对话框的MDL Options选项

MDL Options面板给予用户在读取模型文件时最大的灵活性。在本练习中，所有设置均采用默认设置。

（10）单击Meshing Options for Surface Data按钮，将展开图3-2所示的面板。

除了基本的CAD模型读取功能外，CAD输入工具还提供了使用HyperMesh进行模型表面网格划分的功能。在需要进行接触计算的场合，高质量的表面网格有助于提高仿真结果精度。此外，Launch HyperMesh to create MDL points可以通过HyperMesh将模型中的节点转化为MDL几何点，本练习不使用该功能。

（11）单击Locator Points（Must be in source reference frame）按钮，将弹出图3-3所示的参数选取面板。

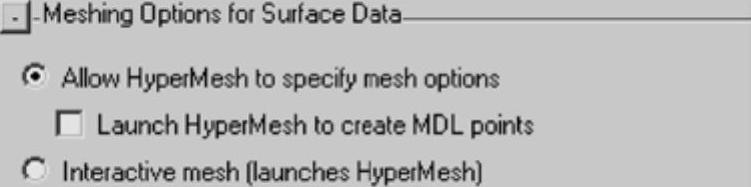
图3-2 Import CAD or FE对话框的 Meshing Options for Surface Data选项

图3-3 Import CAD or FE对话框的 LocatorPoints选项

当CAD模型与MotionView中的模型不在同一坐标系时，用户可应用Locator Points功能，通过指定CAD模型中3个几何点或坐标位置，将CAD模型转换到与MotionView模型相同的坐标系中。

（12）完成上述设置后，单击OK按钮。此时将弹出Import CAD对话框，显示正在读入的CAD模型的体积、密度及质量信息。

（13）将输入模型单位制Input File Length（长度）设置为Millimeter（毫米），使用默认的密度7.83e-6，并单击OK按钮，如图3-4所示。

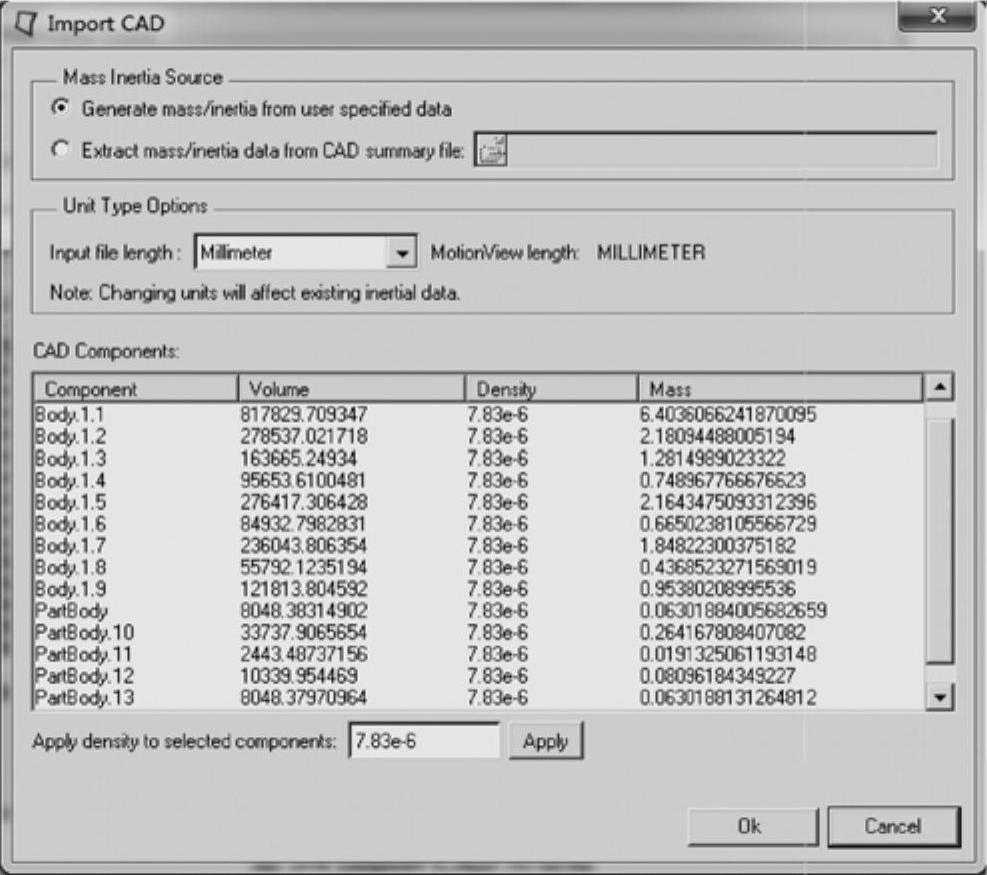
图3-4 Import CAD对话框

（14）当CAD模型成功输入后，用户界面中将弹出如图3-5所示的提示信息。

此时，模型将完整地输入到MotionView前处理界面中的当前活动窗口中。CAD模型中的各个零部件将在MotionView前处理环境中转化为独立的几何体。在CAD模型中，即使是最小的零部件（如螺栓、垫片等）都将作为一个独立的几何体存在于MotionView的模型中。为了控制模型规模，用户需要对其进行适当的整理，将这些较小的几何体与模型中的主要零部件进行连接。

图3-5 模型成功导入提示信息

如果希望进一步减小模型规模，对于体积较小的、转动惯量和质量都可以忽略不计的零部件，可以直接删除，由此对计算结果产生的影响可以忽略不计。

（15）单击“确定”按钮，关闭导入信息提示对话框。

（16）单击Close按钮，关闭Message Log对话框。

（17）选择Tools→Check Model命令，检查模型并为转换的对象赋予编号。

（18）在模型浏览树中，单击Model，并单击展开模型树。右击编号为30102的几何体，在弹出的快捷菜单中选择Rename命令，将其重命名为Wheel，如图3-6所示。

注意：如果CAD模型导入时，默认名称与本实例不同，则可使用编号选择对象。

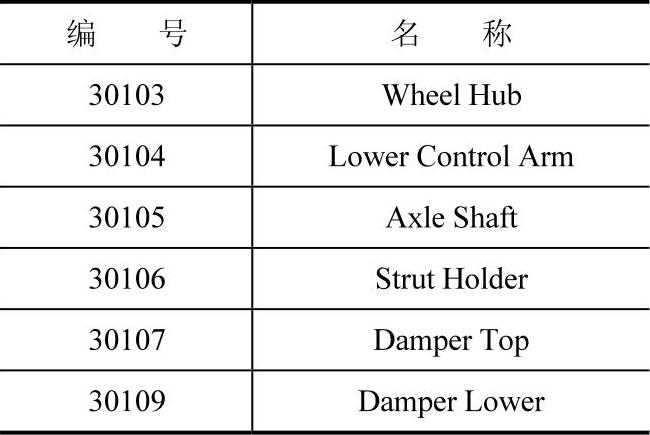
（19）用同样的方法对模型中其他的几何体，进行重新命名操作。Body名称对应关系如表3-1所示。

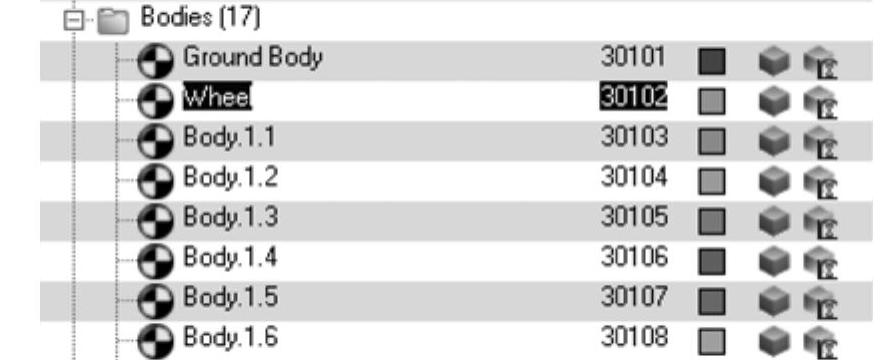
图3-6 Body重命名

表3-1 Body名称对应关系

（20）在模型浏览树中展开Graphics文件夹，并单击最后一个图形文件（编号为90015）。

（21）在Connectivity面板中单击Body，并选择Strut Holder。

（22）在模型浏览树中展开Bodies文件夹，右击编号为30117的几何体，并选择Delete命令，删除这个几何体。

（23）重复步骤（20）～（22），根据表3-2的提示信息，对Graphic图形文件与Body之间的关联性进行调整，并删除不必要的Body对象。

表3-2 Graphic与Body关联性

（续）

注意：在后续的建模环节中，需要在Body Damper Top和Body Damper Lower之间建立弹簧阻尼单元，因此本模型并不需要编号为30111的几何体。

（24）删除编号为30111的几何体。在删除该几何体时，将会弹出相应的对话框，提示是否同时删除与该几何体相关联的图形文件，单击Yes按钮。

完成以上操作后，模型已处于最简状态。

（25）将模型保存为front_susp.mdl。

Body创建完毕后，需要创建几何点用于定位铰。这里，可以使用批处理方法创建点。

（26）在View菜单中选择Command Window命令。

（27）在命令窗口右击，选择File→Load File命令。

（28）选择工作文件夹下的Point_Import.tcl脚本。

（29）选择工作文件夹下的suspension_points.csv文件，该文件包含了几何点的坐标信息。

（30）单击Open按钮。

通过脚本，自动完成了几何点创建。

（31）在View菜单中单击Command Window，关闭命令窗口。

（32）保存模型。

STEP 02 创建铰链

（1）在模型浏览树中右击Model，并选择Add Constraint→Joint命令（或右击Model_- Costaint工具栏的Joints按钮 ），弹出Add Joint or JointPair对话框。

（2）设置Label为Wheel Spindle RJ，Variable为j_whl_spindle_revj。

（3）在Type中选择Revolute Joint。

（4）单击OK按钮。

（5）在主面板的Joint面板中，选择Wheel作为Body1；选择Wheel Hub作为Body 2；单击

Origin处的Point，选择Point8；单击Alignment axis处的Point，选择Point20，如图3-7所示。

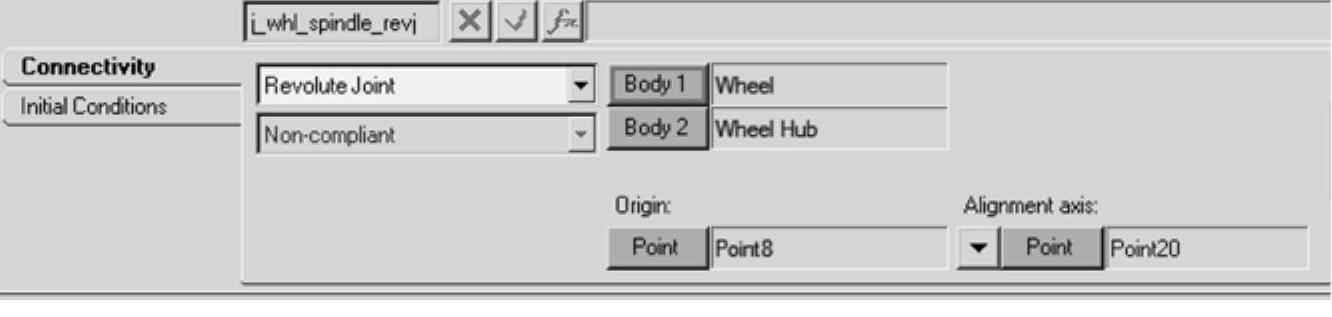
图3-7 Joint面板（步骤5）

（6）类似地，按表3-3所示的内容，使用默认的变量名，继续创建铰链。

表3-3 铰链参数

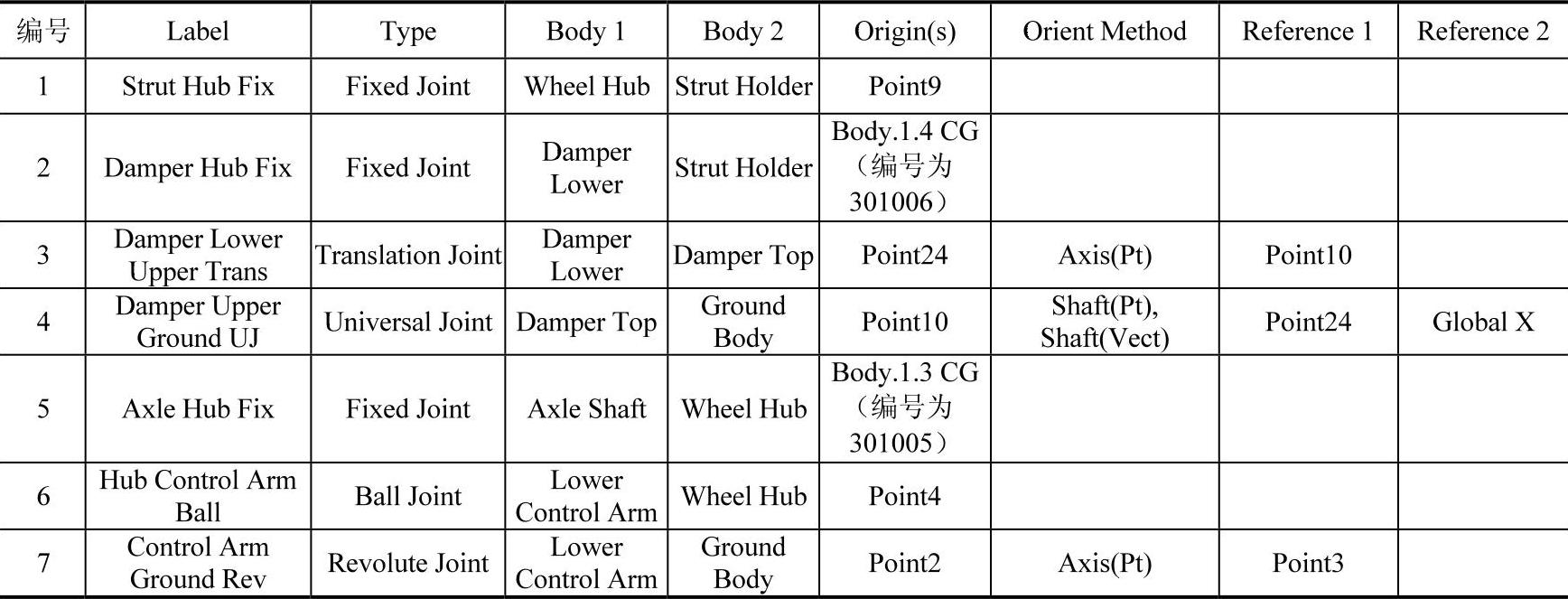
注：选择Ground Body时，可以使用鼠标单击图形区的全局坐标系。类似地，可以选取全局坐标系的某个轴线作为铰的指向。

STEP 03 创建弹簧阻尼单元

（1）在模型浏览树中右击Model，并选择Add Force Entity→Spring Dampers命令（或在Model-Force工具栏中右击Spring Dampers按钮），弹出Add SpringDamper or Spring DamperPair对话框。

（2）定义Label为Strut-SpringDamper，定义Variable为sd_strut，指定弹簧类型为Coil Spring（拉簧）。

（3）单击OK按钮。

（4）在主菜单的SpringDamper面板中单击Body1，选择Damper Top；单击Body2中，选择Damper Lower。

（5）在Point1和Point2中，分别选择Point10和Point1。

（6）在Measure Between Points中，注意两点的距离应为259.942，如图3-8所示。

图3-8 SpringDamper面板

（7）在Preload标签中，定义Free Length为259.942。

（8）在Properties标签中，设置stiffness（K Linear）为10，damping（C linear）为0.1。

（9）在模型浏览树中右击Model，并选择Add Reference Entity→Graphic命令（或右击Model-Reference工具栏中的Graphic按钮）。

（10）在Label中，输入Spring，并接受默认的变量名。在Type中，选择Spring。

（11）单击OK按钮。

（12）在Connectivity面板中，选择Strut-SpringDamper作为其Parent。

（13）选择Point10及Point1作为该Graphic文件的Point1和Point2，如图3-9所示。

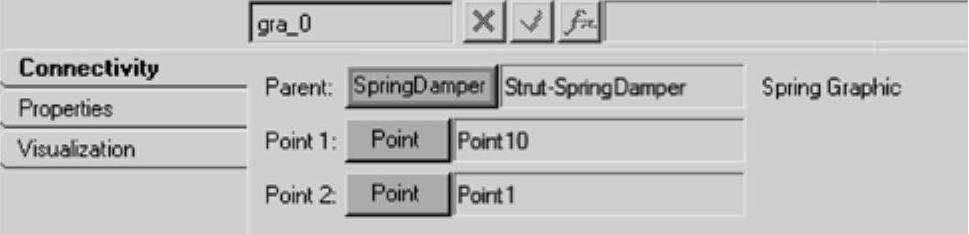
图3-9 Graphic面板

（14）单击Properties标签，在Radius中输入40，在Coils中输入10。

STEP 04 创建台架

本步将创建用于施加向车轮往复运动的台架。

（1）在模型浏览树中右击Model，并选择Add Reference Entity→Body命令（或在Model-Reference工具栏中右击Body按钮），弹出Add Body or BodyPair对话框。

（2）指定Body的Label为Jack Dummy，Variable为b_jdummy。

（3）单击OK按钮。

（4）在Body面板的Properties标签中指定质量及转动惯量，如图3-10所示。

图3-10 Body面板(www.daowen.com)

（5）进入CM Coordinates面板，选中Use center of mass coordinate system复选框。

（6）指定Origin为Point11。

（7）在模型浏览树中右击Model，并选择Add Reference Entity→Graphic命令（或右击Model-Reference工具栏中的Graphic按钮）。

（8）在弹出的Add Graphic or GraphicPair对话框中设置Label为Jack Plate，并选择其Type为Cylinder，接受其他的默认设置并单击OK按钮。

（9）在Connectivity面板中，设置其Parent Body为Jack Dummy。

（10）将Origin设置为Point11，将Direction设置为Point8，如图3-11所示。

图3-11 Graphic面板（步骤10）

（11）激活Properties标签，将Autolen切换为Length，并指定其为-30。

（12）在Radius 1中输入250。

（13）在模型浏览树中右击Model，并选择Add Constraint→Joint命令（或右击Model_- Constraint工具栏中Joint按钮）。

（14）在弹出的Add Joint or JointPair对话框中设置Label为Jack Wheel Inplane，设置Variable为j_jack_wheel。在Type下拉菜单中，选择Inplane Joint。

（15）单击OK按钮。

（16）在Connectivity标签的Body1中指定Wheel，在Body2中指定Jack Dummy，在Origin中指定Point11，在Normal中指定Point8，如图3-12所示。

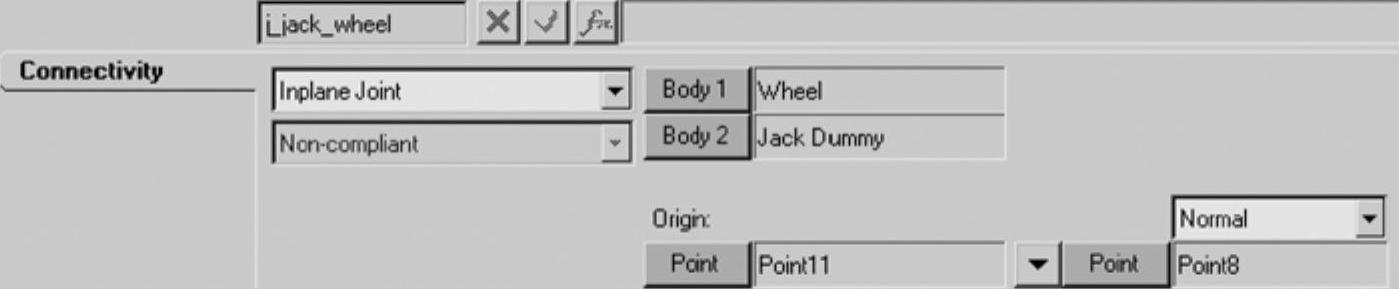
图3-12 Joint面板（步骤16）

（17）新建另一铰链，其Label设置为Jack Ground Trans，其Variable设置为j_jack_grnd，其类型Type选择为Translational Joint。

（18）单击OK按钮。

（19）在Connectivity面板的Body1中选择Jack Dummy，在Body2中选择Ground Body，在Orgin中选择Point11，在Axis中选择Point8，如图3-13所示。

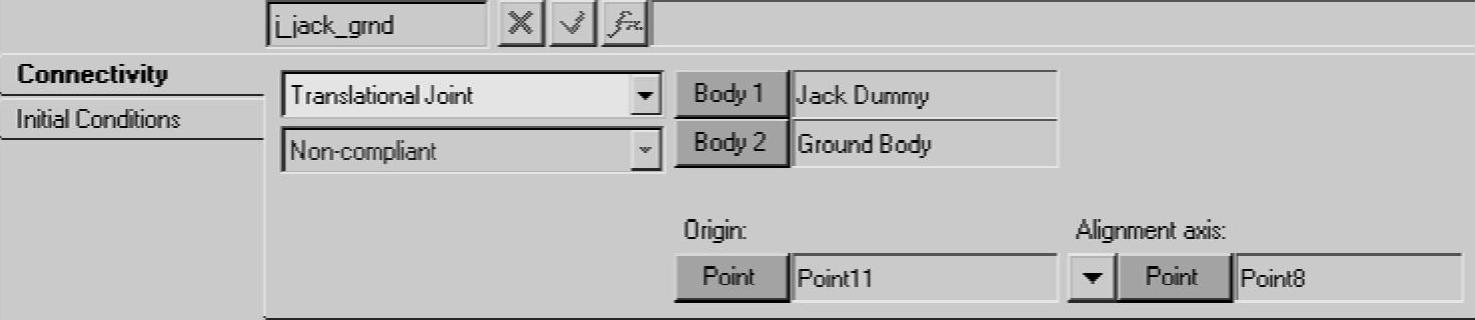
图3-13 Joint面板（步骤19）

（20）至此，所有连接定义完毕，前悬架模型如图3-14所示。

图3-14 前悬架模型

（21）保存模型。

STEP 05 定义输入条件，并递交求解

本步骤将创建驱动约束，并定义结果输出请求。

（1）在模型浏览树中，右击Model，选择Add Constraint→Motion命令（或在Model_- constraint工具栏中右击Motion按钮）。

（2）在弹出的Add Motion对话框中，设置Label为Jack Motion，设置Variable为mot_jack。

（3）在Connectivity面板的Joint中指定Jack Ground Trans，如图3-15所示。

图3-15 Motion面板

（4）在Properties标签中，指定激励加载方式为Expression，激活表达式文本框，输入`50*sin（TIME）`作为位移驱动函数。

（5）创建另一个驱动约束，设置Label为Wheel Spindle，设置Variable为mot_wheel。

（6）在Connectivity标签中的Joint中选择Wheel Spindle RJ。

图3-16 Joint面板（步骤6）

（7）在Properties标签的Motion中输入0。转角为0，保证了Wheel不会绕着其轴自由转动。

（8）在模型浏览树中，右击Model，选择Add General MDL entity→Output命令（或在Model-General工具栏中右击Output按钮）。

（9）在弹出的Add Output对话框中，设置Label为Wheel_center，设置Variable为o_disp。

（10）单击OK按钮。

（11）在Output面板中，选择输出结果为Displacement，指定Body1为Wheel，Body2为Ground Body；pt on Body1为Wheel的质心Body.1 CG（如不一致，可使用编号选取，该几何点编号为301002），其他保留默认设置，如图3-17所示。

（12）保存模型。

（13）单击Run按钮，进入Run面板。

（14）在Main标签中单击“文件浏览”按钮，指定求解器输入文件的名称（front_susp.xml）与路径。

图3-17 Output面板

（15）在Sim Type下拉菜单中的求解类型中选择Static+Transient。

（16）单击Check按钮，检查模型构成、系统自由度、是否有未定义质量的构件以及过约束情况等。

注意：在默认情况下，MotionView仅提示模型中的错误信息及警告信息。如需检查系统自由度，则可选择Tools→Options命令，进入Check Model选项，选中Degrees of Freedom复选框。

（17）确定模型没有错误后，单击Run按钮。

（18）完成求解后，单击Animate按钮进入HyperView后处理界面。HyperView将自动加载计算结果。

（19）单击Plot按钮，单击窗口3，进入HyperGraph后处理界面。根据图3-18，绘制轮心位移曲线。

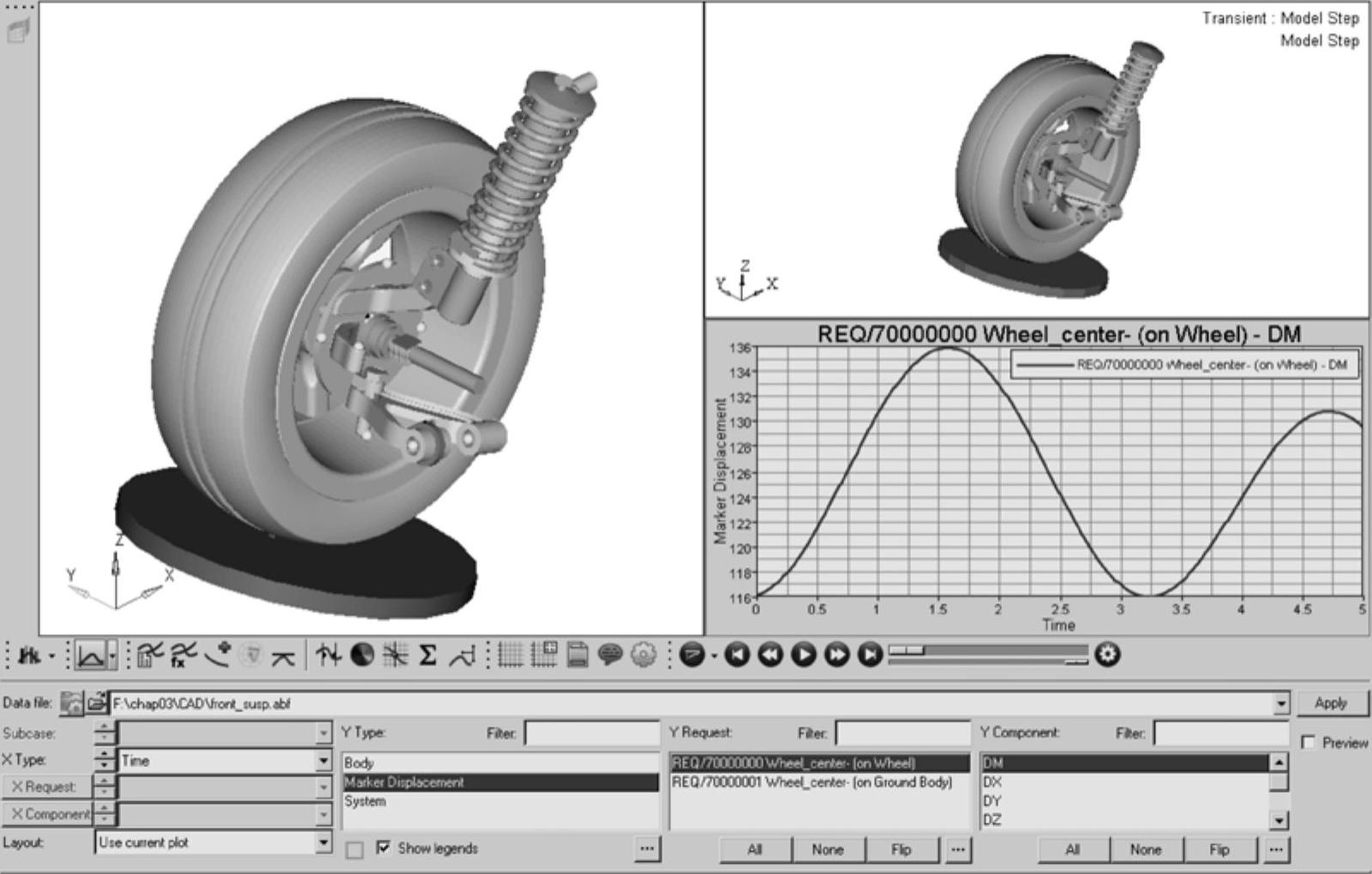
图3-18 仿真结果

注：MotionSolve提供了瞬态（Transient）分析、静态（Static）分析、准静态（Quasi_- Static）分析以及线性模态（Linear）分析4种仿真类型。

1.瞬态分析

在瞬态分析中，求解器将根据系统自由度决定进行运动学分析或是动力学分析。

如果系统自由度为0，则进行运动学分析。此时，由系统中各种类型的铰链以及驱动约束构成的代数方程完全确定了机构的运动状态。这些约束及其相对时间的导数常用于计算构件的位移、速度和加速度，根据力平衡方程可计算约束反力。为获得准确的约束反力，需要提供构件实际的质量、质心位置以及转动惯量等信息。使用不正确的质量、转动惯量等信息可获得正确的运动结果，但约束反力值却是错误的。运动学分析的主要目的是获得正确的机构运动结果，而这些参数不会影响运动结果，因此在求解过程中，求解器仅提出警告信息，而不会报错并中断求解过程。

如果系统自由度大于0，则进行动力学分析。动力学分析将求解一系列微分或微分-代数方程组（其中代数方程组来自模型中的约束），获得力与运动之间的关系。MotionSolve支持以下4种类型的方程构成形式。

（1）常微分方程组（ODE）。

MotionSolve通过坐标分离技术将DAE形式的运动方程转换为ODE形式，并提供了刚性（VSTIFF和MSTIFF）和非刚性求解器（ABAM）。

（2）指标3方程（Index-3）。

指标3方程方法可将微分—代数方程组（DAE）直接提交给求解器。MotionSolve使用DASPK积分器求解指标3形式的机构运动方程。在求解过程中，该方法不会监测机构速度及加速度状态的积分误差，因而求解速度快，但速度项和加速度项结果存在一定误差。

（3）指标2方程（Index-2）。

指标2方程方法提供了一种稳定的微分—代数方程组给求解器。MotionSolve使用DASPK积分器求解指标2形式的机构运动方程。在求解过程中，该方法将监测机构位移及速度状态的积分误差，结果精度高，但求解速度相对指标3方法稍慢。

（4）指标1方程（Index-1）。

指标1方程方法作为指标2方程方法的扩展，提供了一种更加稳定的微分—代数方程组给求解器。“稳定”是指方程求解过程中除了位移和速度约束，还加入了加速度约束，因此相对于指标2方程方法，指标1方程方法结果精度更高，但求解速度更慢。MotionSolve使用DASPK积分器求解指标1形式的机构运动方程。

2.静态分析

静态分析用于寻找系统的静平衡位置。静平衡指系统承受的所有力与力矩平衡的状态。MotionSolve提供了两种静态分析算法。

（1）最大动能方法（MKEAM）。

根据动力学问题构建模型，去掉模型中所有阻尼。此时将获得一个保守系统，即系统能量（由动能与势能构成）保持不变。

1）启动数值积分，监测系统动能。如果监测到最大动能，停止积分并回退精确定位最大动能的时刻。由于系统是保守的，最大动能发生的时刻即是最小势能产生的时刻。

2）此时，将所有的速度和加速度设置为零，产生零动能。然后重启积分程序。

3）步骤1）～2）构成一个完整的迭代，如果找到的最大动能是理想最大动能，则系统已处于平衡位置。然而，由于积分器的离散特性，实际求解过程并不是如此顺利。因而需要重复进行上述迭代直至满足下述收敛准则。

●最大动能误差（Max K.E.Tol.）：指两次迭代中最大动能的改变量。

●最大位移误差（Max Delta q Tol.）：指两次迭代中广义坐标的最大改变量。

●最大迭代次数（Max Iterations）：指求解停止前进行迭代的最大次数。

MKEAM方法有以下优势：

●只寻找稳定的平衡位置。

●适用于平衡位置远离装配位置的系统。

（2）力不平衡方法（Force Imbalance Method，FIM）。

力不平衡方法将运动方程中所有的速度和加速度项设置为零，以获得一个非线性系统方程（其中广义坐标和约束力是未知量），然后使用Newton-Raphson算法寻找平衡位置。

与MKEAM类似，FIM方法也可以用于寻找稳定和不稳定的平衡位置。但是，FIM方法在处理平衡位置离装配位置较远的情况或模型有不连续因素作用的场合时，会有困难。因而MKEAM和FIM方法是互补的。MotionSolve提供了3种FIM方法：

●FIM_E是原始的力不平衡方法，不支持所有的MotionSolve对象。

●FIM_S是一种修正的力不平衡方法，支持除Force_Contact之外的所有MotionSolve对象。

●FIM_D是一种基于时间积分的准静态方法，不是一种完全静态的解决方案。除了使

用Param_Static指定的参数，FIM_D还使用Param_Transient中定义的参数来控制DAE的积分过程。如果需要一种完全静态的解决方案，FIM_D将自动转到FIM_S。

3.准静态分析

在真实世界中，准静态指系统缓慢运动，不会产生任何动态效应。在数学意义上，准静态分析是给定时间内一系列静态分析的组合。当需要在含有时变载荷或驱动的系统中寻找一系列静平衡位置时，准静态分析非常有用。

分析开始时，模型当前装配位置作为起始点，应用力不平衡方法计算模型平衡位置，因而系统中不再出现不平衡力或力矩，所有的运动约束均满足。这一位置将作为下一次分析的起始。求解器将严格根据用户指定的步长求解模型，太大的步长可能导致收敛失效。

4.线性分析

MotionSolve线性分析提供以下功能：

（1）用于稳定性或振动分析。

MotionSolve线性分析可在以下位置进行模型线性化并计算系统特征值与正则模态。

●模型装配位置。

●模型静平衡位置。

●瞬态分析结束位置。

特征值用于预测系统稳定性以及共振频率，正则模态用于研究振动系统的运动情况。

（2）用于控制系统设计。

通过线性化分析获得一个简化的系统，定义系统输入/输出，然后使用MotionSolve可获得系统的状态空间描述。

系统输入/输出可由Control_PlantInput和Control_PlantOutput分别定义。应用Param_Linear命令启动线性分析，产生如下结果：

●MATLAB格式的A、B、C、D矩阵，分别写入以*.a、*.b、*.c和*.d为扩展名的文件中。

●状态空间形式的线性系统写入.mdl格式的Simulink模型文件（该文件与MotionView模型文件的扩展名相同）。

●特征值写入*.eig文件。

●每个特征向量对应一个.mrf文件。该文件与MotionView模型动画文件（.maf）一起用于描述系统的振型动画。