（一）混合加密体系

公开密钥算法由于解决了对称加密算法中的加密和解密密钥都需要保密的问题，在网络安全中得到了广泛的应用。

但是，以RSA算法为主的公开密钥算法也存在一些缺点。例如，公钥密钥算法比较复杂。在加密和解密的过程中，由于都需要进行大数的幂运算，其运算量一般是对称加密算法的几百、几千甚至上万倍，导致了加密、解密速度比对称加密算法慢很多。因此，在网络上传送信息特别是大量的信息时，一般没有必要都采用公开密钥算法对信息进行加密，这也是不现实的。一般采用的方法是混合加密体系。

在混合加密体系中，使用对称加密算法（如DES算法）对要发送的数据进行加、解密，同时，使用公开密钥算法（最常用的是RSA算法）来加密对称加密算法的密钥，如图4-9所示。这样，就可以综合发挥两种加密算法的优点，既加快了加、解密的速度，又解决了对称加密算法中密钥保存和管理的困难，是目前解决网络上信息传输安全性的一个较好的解决方法。

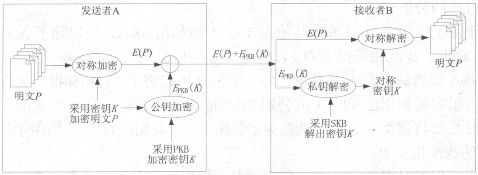
图4-9　混合加密体系

（二）数字签名

在计算机网络上进行通信时，不像书信或文件传送那样，可以通过亲笔签名或印章来确认身份。经常会发生这样的情况：发送方不承认自己发送过某一个文件；接收方伪造一份文件，声称是对方发送的；接收方对接收到的文件进行篡改，等等。那么，如何对网络上传送的文件进行身份验证呢？这就是数字签名所要解决的问题。

一个完善的数字签名应该解决好下面3个问题。

（1）接收方能够核实发送方对报文的签名，如果当事双方对签名真伪发生争议，应该能够在第三方面前通过验证签名来确认其真伪。

（2）发送方事后不能否认自己对报文的签名。

（3）除了发送方的其他任何人不能伪造签名，也不能对接收或发送的信息进行篡改、伪造。

满足上述3个条件的数字签名技术就可以解决对网络上传输的报文进行身份验证的问题了。

数字签名的实现采用了密码技术，其安全性取决于密码体系的安全性。现在，经常采用公钥密钥加密算法实现数字签名，特别是采用RSA算法。下面简单地介绍一下数字签名的实现思想。(www.daowen.com)

假设发送者A要发送一个报文信息P给B，那么A采用私钥SKA对报文P进行解密运算（注意：读者可以把这里的解密只是看成一种数学运算，而不是非要经过加密运算的报文才能进行解密。这里，发送者A并非为了加密报文，而是为了实现数字签名），实现对报文的签名。然后将结果DSKA（P）发送给接收者B。B在接收到DSKA（P）后，采用已知A的公钥PKA对报文进行加密运算，就可以得到P=ESKA（DSKA（P）），核实签名，如图4-10所示。

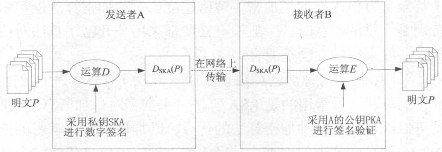
图4-10　数字签名的实现示意图

对上述过程的分析如下。

（1）由于除了发送者A外没有其他人知道A的私钥SKA，所以除了A外没有人能生成DSKA（P），因此，B就相信报文DSKA（P）是A签名后发送出来的。

（2）如果A要否认报文P是其发送的，那么B可以将DSKA（P）和报文P在第三方面前出示，第三方很容易利用已知的A的公钥PKA证实报文P确实是A发送的。

（3）如果B要将报文P篡改、伪造为Q，那么，B就无法在第三方面前出示DSKA（Q），这就证明B伪造了报文P。

上述过程实现了对报文信息P的数字签名，但报文P并没有进行加密，如果其他人截获了报文DSKA（P），并知道了发送者的身份，就可以通过查阅文档得到发送者的公钥PKA，因此获取报文P的内容。

为了达到加密的目的，可以采用下面的模型：在将报文DSKA（P）发送出去之前，先用B的公钥PKB对报文进行加密；B在接收到报文后，先用私钥SKB对报文进行解密，然后再验证签名。这样，就可以达到加密和签名的双重效果，如图4-11所示。

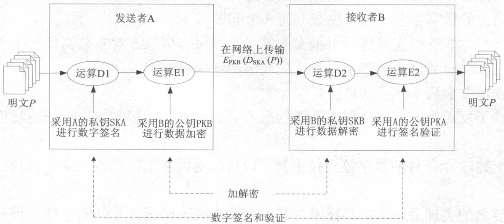
图4-11　具有保密性的数字签名实现示意图

目前，数字签名技术在商业活动中得到了广泛的应用，所有需要手动签名的地方，都可以使用数字签名。例如，使用电子数据交换（Electronic Data Interchange，EDI）来购物并提供服务，就使用了数字签名。再如，中国招商银行的网上银行系统，也大量地使用了数字签名来验证用户的身份。随着计算机网络和Internet在人们生活中所占的地位逐步提高，数字签名必将成为人们生活中非常重要的一部分。