David Chaum提出了密码学家晚餐问题：三位密码学家正坐在他们最喜欢的三星级餐馆准备吃晚餐。侍者通知他们晚餐需匿名支付账单。其中一个密码学家可能正在付账，或者可能已由美国国家安全局NSA付过了。这三位密码学家都尊重彼此匿名付账的权利，但他们要知道是不是NSA在付账。假设这三个密码学家分别叫Alice、Bob和Carol，他们怎样才能确定他们之中的一个正在付账同时又要保护付账者的匿名呢？

这个问题可以这样解决：每个密码学家在他的菜单后，在他和他右边的密码学家之间抛掷一枚硬币，以致只有他们两个能看到结果。然后每个密码学家都大声说他能看到两枚硬币——他抛的一个和他左手邻居抛的那个——落下来是同一面还是不同的一面。如果有一个密码学家付账，他就说所看到的相反的结果。在桌子上说不同的人数为奇数表明有一个密码学家在付账；不同为偶数表明NSA在付账（假设晚餐只付一次账）。还有，如果一个密码学家在付账，另外两个人都不能从所说的话中得知关于那个密码学家付账的任何事。

为了明白这是如何起作用的，不妨想象Alice试图弄清其他哪个密码学家为晚餐付了账（假设既不是她也不是NSA付的）。如果她看见两个不同的硬币，那么另外两个密码学家Bob和Carol或者都说“相同”，或者都说“不同”（记住，密码学家说“不同”的次数为奇数，表明他们中有一个付了账）。如果都说“不同”，那么付账者是最靠近与未看见的硬币不同的那枚硬币的密码学家。但是，如果Alice看见两枚硬币是相同，那么或者Bob说“相同”而Carol说“不同”，或者Bob说“不同”而Carol说“相同”。如果未看见的硬币和她看到的两枚硬币是相同的，那个说“不同”的密码学家是付账者。如果隐藏的硬币和她看到的两枚硬币是不同的，那么说“相同”的密码学家是付账者。在所有这些情况中，Alice都需要知道Bob和Carol抛掷硬币的结果以决定是他们中的哪一位付的款。图11.1描述了上面的过程，Crypt（i）（i=0，1，2）与Coin（i）（i=0，1，2）分别表示密码学家和硬币结果，Crypt（i）两边的硬币如果是相同的用0表示，不同则用1表示。若Crypt（i）付款，则说假话输出为Coin（i-1）⊕Coin（i）⊕1；Crypt（i）没付款说真话输出Coin（i-1）⊕Coin（i），所有输出进行异或，最后结果如果为1表示有人付款，为0表示无人付款。

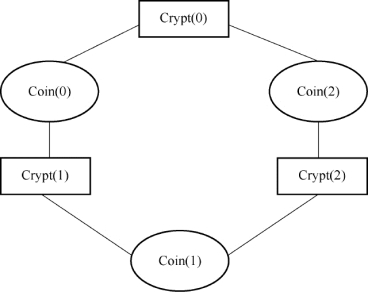
图11.1　密码学家晚餐问题

这个协议可以推广到任意数量的密码学家：他们全都坐成一圈并在他们中抛掷硬币。甚至两个密码学家也能执行这个协议，当然他们知道谁付的账，但是观看这个协议的人只知道是一个密码学家付的账还是NSA付的账，他们不会知道是哪个密码学家付的账。

这个协议可以应用到匿名消息广播。这是一个无条件的发方和收方不可追踪性的例子。在网络上的一群用户可以用这个协议发送匿名报文。(www.daowen.com)

（1）用户把他们自己排进一个逻辑圆圈。

（2）在一定的时间间隔内，相邻的每对用户对在他们之间抛掷硬币，使用一些公正的硬币抛掷协议防止窃听者。

（3）在每次抛掷之后每个用户说“相同”或“不同”。

（4）如果一个实体想发送“0”，他会声明真相，否则，就撒谎。“0”和“1”将形成匿名报文消息。

如果消息由一个节点的公钥加密，则发送方和接收方都将是匿名的。

这个协议的一个问题是若多个人同时想发送匿名报文，则出现冲突，协议失败。另外一个恶意的参与者虽然不能读出报文，但他总能通过在第（3）步中说谎来破坏系统。