郑玉良于1997年在信息安全研讨会上首次提出了签密的概念及方案（基于DSS协议），其基本思想是在同一个逻辑步骤内同时完成数字签名和加密两项功能，而且加解密仍可采用效率较高的对称密码算法，因而其代价要远远低于“先签名后加密”，并且同时可实现密钥的安全传输，所以是实现对信息既保密又认证的较为理想的方法。

（1）系统公开参数p为大素数；q为p-1的大素因子；g∈[1，p-1]且在模p下的阶为q；hash为单向Hash函数，其输出至少为128 bit；KH为具有密钥k的单向Hash函数，常取KHk（m）=Hash（k，m）；（E，D）为一对对称加密及解密算法。

（2）发送方密钥和接收方密钥

发送方随机选取xA∈[1，q-1]作为私钥，公钥为yA=gxA；接收方随机选取xA∈[1，q-1]作为私钥，公钥为yB=gxB；最后公开（yA，yB）。

算法过程如表7.1所示。

表7.1　郑玉良的签密及验证算法

此方案的缺点在于只有接收者才能对所接收的信息进行验证。因此，F.Bao和R.H.Deng在1998年对上述方案作了一些改进（如表7.2所示），使得第三方验证者在知道消息m的情况下可以对签密进行验证。(www.daowen.com)

表7.2　F.Bao和R.H.Deng改进的签密方案

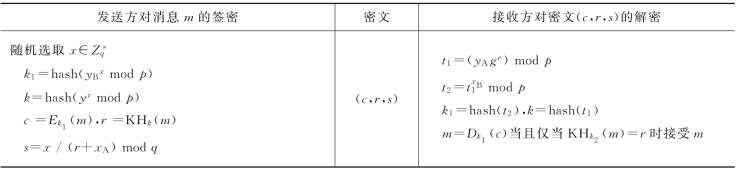
在这个方案中，接收者可将（m，r，s）发给第三方验证者V，V可通过验证k=hash（yA gr）s mod p和r=KHk（m）来判断消息是否来自发送者，但验证者V将需要知道m。这将限制验证者的身份。

所以，C.Gamage、J.Leiwo和郑玉良在1999年对上面的签密方案做了进一步的改进（如表7.3所示），使得任何验证者V都可以对签密进行验证，即实现了公开验证。

表7.3　可公开验证的签密方案

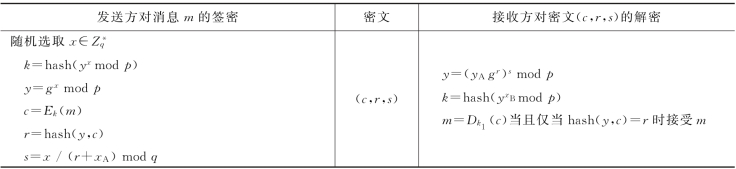
验证者V可由（c，r，s）和y=（yA gr）s mod p来验证，验证通过当且仅当hash（y，c）=r成立，并且验证者不需要知道信息m，这就达到了公开验证的目的。