批签名是指能够用一次签名动作完成对若干个不同消息的签名。并且以后可以对每一条消息独立地进行认证。这类签名算法提高了对批量文件签名的效率，有时候会应用在电子商务的某些领域。

1.Batch RSA方案描述

Amos Fiat最早提出了批签名的概念，并于1990年提出了Batch RSA方案。该方案基于RSA算法，其产生RSA签名结果。该方案中，签名者拥有若干个私钥指数，并且这些指数之间两两互素。

签名可以描述为三个阶段：

（1）把若干个消息合并成一个待签名的消息M。合并方法是求每个消息的低指数的幂的乘积。

（2）对消息M签名。

（3）在总的签名结果上划分出每一条消息的签名。

我们用两个消息为例来理解上述过程。消息为m1、m2，相应的公钥指数为e1、e2。对应上述三个阶段分别如下：

2.Bi-tree批签名方案

澳大利亚学者C.J.Pavlovski和C.Boyd使用Merkle哈希树提出的Bi-tree批签名方案可以方便地把其他普通数字签名算法改造为批数字签名。相对于以前的批签名，Bi-tree批签名方案克服了基于某种特定的签名算法、消息数目有一定的限制等缺点。这个方案对消息数目没有限制，方案中可以使用其他普通的签名算法。

（1）方案概况

方案中使用了二叉树和两个特殊的散列函数。签名部分可以分为三部分：对各个消息用散列函数处理出一个最终的总散列值M；用一般的签名算法对M签名；对不同的消息计算其余部（余部作为该消息的签名的一部分）。

认证部分可以划分为两个部分：用该条消息和其签名的余部计算出一个值（也就是上述的总散列值M）；用对应的签名认证算法进行验证。

（2）求总散列值

方案中使用了两个散列函数h0、h1，当然要求它们是抗冲突的。如果有一个抗冲突的散列函数h，那么可以简单地构造出两个相互抗冲突的散列函数h0、h1。例如，可以定义：h0（x）=h（0‖x），h1（x）=h（1‖x），其中符号‖表示连接。如果假设它们不是互抗冲突的，那么可以找到两个值x和y满足：h0（x）=h1（y），就有h（0‖x）=h（1‖y），而h是抗冲突的，所以假设不成立。

现在有一批消息（m1，m2，…，mk），下面介绍如何求其总的散列值。

生成一个二叉树，给其每一个叶节点赋予一个消息的散列值。下面计算各父节点的值，左子节点的值连接右子节点的值然后求出对于h1的散列值。如此，从叶节点开始直至根节点，根节点的值就是所求的总散列值。总之，散列函数h0仅仅用于处理叶节点，而其他非叶节点用散列函数h1处理。

图7.4显示了一个处理三个消息m1、m2和m3的情况。

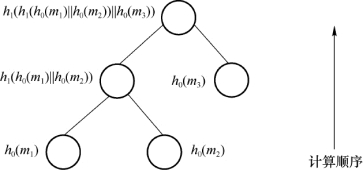
图7.4　三条消息求散列值的二叉树

注意到图中叶节点使用的是散列函数h0。其计算的顺序是从叶节点到根节点从下向上的顺序。根节点的值相当于所有消息的散列值。

（3）签名过程

①使用签名的方法求出所有消息的总散列值M。

②用一个选定的普通签名算法对总散列值M签名，生成S。(www.daowen.com)

③生成各条消息的对应签名余部。

每一条消息的各自签名余部都是不相同的，构成如下：从该叶节点到根节点的路径中各个节点的兄节点，以及该兄节点的左/右标志（可用L/R或比特0/1表示）。例如图7.4中，m1消息的签名余部为res1=（（h0（m2），R），（h0（m3），R））。

最后签名结果为S加上对应的签名余部，例如上面消息m1的签名为（S，（h0（m2），R），（h0（m3），R））。

下面介绍求取余部的算法。

假设消息m1对应的节点深度为d1，其余部假设为r1，r2，…，rd1。为了表述方便，用dir（N）表示节点N的左/右标志，而sib（N）表示其兄节点。那么求取余部的算法可以用为代码表示。

c←h0(m1)

for j←1 to d1 do

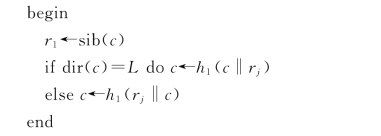
最终，消息m1的签名为（S，r1，dir（r1），r2，dir（r2），…，rd1，dir（rd1）），其中（r1，dir（r1），r2，dir（r2），…，rd1，dir（rd1））为消息余部。

（4）验证过程

验证过程分为两部分：处理签名余部和用普通验证算法验证。接收者在收到消息m和签名（T，s1，t1，s2，t2，…，sd，td）之后，验证过程如下。

①恢复“总散列值c”。

我们可以通过消息m和签名，计算出一个值c，其相当于签名时计算的总散列值。可以用如下伪代码表示该求值过程。

②用对应的普通验证算法验证。

签名合法的情形下，总散列值c的签名结果就假设为T，可以如下理解。先看普通签名人的验证算法，总散列值c的描述为形式

其中，Sig表示签名结果，Pub Key是公钥。那么Bi-tree批签名方案的验证就可以表述为

由于该方案利用了已有的数字签名算法，显然其具有数字签名的特点。另外，选用二叉树，可以有效地减少签名余部的尺寸。

批签名应用的一个例子是使用Merkle哈希树进行数字证书撤销。在数字证书有效期到期之前，证书由于私钥泄露、员工离职等原因需要撤销。对撤销的证书需要CA的签名，如果对每个撤销的证书逐个签名，CA的工作量过大，因此可以使用Merkle Hash树的方式生成证书撤销列表。例如撤销4个数字证书，可按图7.5构造Hash树。这里h是哈希函数，Ci是要撤销的数字证书。根哈希值h（1，4）公开，CA对h（1，4）进行签名，签名一次就可以撤销4个数字证书。

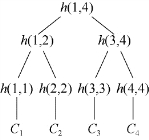
图7.5　使用Merkle Hash树进行数字证书撤销