上面的数字签名方案不支持选择性泄露，如果Alice在她的数字证书中声明一个属性，Bob如何知道这个声明是正确的呢？Alice的数字签名不仅证明她知道一个秘密密钥，而且证明证书中的属性与她的声明是一致的。一般的零知识证明在这里没有作用，因为声明的属性必须编码成门电路，辅助的属性必须用于每个门中。Brands提出了一个解决方案，图6.9中的知识证明在这里仍然起作用，我们把（x1，…，xl，α）叫作h关于底元组为（g1，…，gl，h0）的表示法。

图6.10　x1=y1的签名证明

F的Hash表示对Alice要证明的属性的描述是唯一的。如果可能被证明的属性都是x1=y1 mod q的形式，那么它与y1一起进行Hash。如果没有F，Alice会以图6.9中的方式形成a和r2，…，rl+1，结果就是证明y1=x1+（w1/H（h，a，m））mod q。F与y1一起Hash保证了y1不可能在c形成之后被重构。

在这个协议中，不管x1，…，xl是以何种方式选取的，Bob在x1=y1 mod g的形式下都不能获知Alice属性的任何信息。

1.线性关系的证明

如果Alice想要一次使Bob确信她的多个属性，只需将上面的方案做些改变即可，Alice甚至可以通过AND证明形成线性关系的属性规则，而这是很有实际意义的，原因有两点。(www.daowen.com)

图6.11　（x1=2x3+3 mod q）AND（x2=4x3+5 mod q）的签名证明

2.否认证明

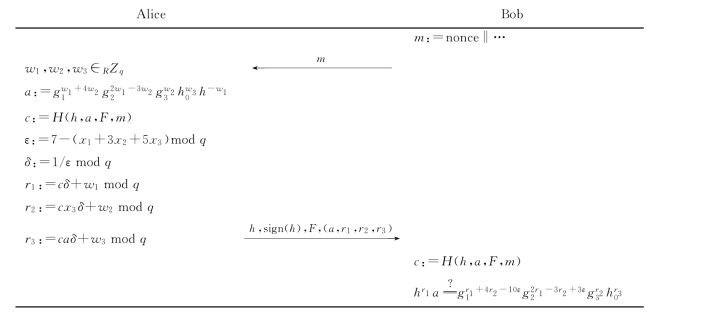
图6.12　NOT（x1+3x2+5x3=7 mod q）AND（3x1+10x2+18x3=23 mod q）的签名证明