由于Merkle树存在效率低下的缺点，因此有必要作改进。因为在实际的应用中证书上每一个属性字段被出示的概率是不一样的。根据调查（如图6.6所示），不同字段出示的概率是不一样的。一般来说E-mail、姓名等被展示次数是比较多的，而体重、性别、住址等被展示次数相对来说比较少。因此，根据这个特点，我们用Huffman树对Merkle树进行进一步的修改。

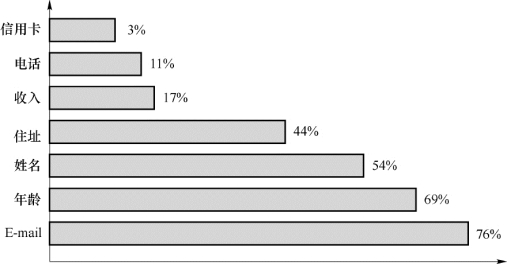
图6.6　实际应用中不同字段出现概率的统计

Huffman树是一个有权二叉树，其生成算法如下。

（1）由给定的n个权值{w0，w1，w2，…，wn-1}，构造具有n棵扩充二叉树的森林F={T0，T1，T2，…，Tn-1}，其中每一棵扩充二叉树Ti只有一个带有权值wi的根节点，其左右子树均为空。

（2）重复以下步骤，直到F中仅剩下一棵树为止：

①在F中选取两棵根节点的权值最小的扩充二叉树作为左右子树，构造一棵新的二叉树，置新的二叉树的根节点的权值为其左右子树上根节点权值之和；

②在F中删去这两棵二叉树，把新的二叉树加入F。

为了说明的简单，我们假定Alice的证书上仍然只有4个属性：姓名（Alice）、E-mail（Alice@163.com）、性别（女）、生日（1980-8-8）。假定在20次会话中，E-mail需要出示20次，姓名需要出示12次，性别需要出示5次，而生日需要出示1次。那么根据Huffman编码算法，E-mail、姓名、性别、生日相应的权值就是{20，12，5，1}，生成相应的Huffman树，如图6.7所示。图中4个叶子节点代表着不同属性的权值，生成的方法与原来的方案类似，即先生成4个随机数rv1、rv2、rv3、rv4，然后和每一个属性字段作连接并添加特殊标志符号“*”，这就生成4个临时值tv1=Alice*rv1；tv2=Alice@163.com*rv2；tv3=女*rv3；tv4=1980-8-8*rv4，对这4个值Hash，就生成4个叶子节点，这4个叶子节点再根据Huffman编码算法构造成Huffman树。

如果Bob需要Alice的E-mail，Alice将发送tv1、node2。Bob需要下面两个步骤：

（1）计算leaf1′=Hash（tv1），root′=Hash（leaf1′‖node2）；

（2）比较root′和root，确认无误后，再通过特殊标志“*”从tv1中取得E-mail信息。(www.daowen.com)

如果使用Merkle树，Alice要发送tv1、leaf2、node2（如图6.7所示）。Bob需要下面3个步骤：

（1）计算leaf1′=Hash（tv1），node1′=Hash（leaf1′‖leaf2）。

（2）计算root′=Hash（node1′‖node2）。

（3）比较root′和root。

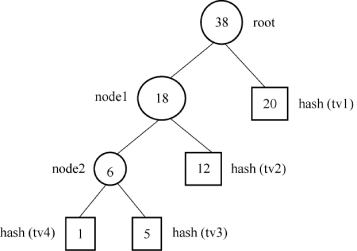
图6.7　Huffman树解决方案

因为Merkle树没有考虑节点出示的概率问题，因而每一个属性在树中的深度是一样的；而Huffman树考虑到了每个节点出示的概率，这就使得出示概率高的节点在树中的深度要比出示概率低的节点要低，从而减少了树的搜索路径长度，提高了效率。但不足之处是应用Huffman树构建时，每个节点的权值（出示概率）是根据长期统计得来的，因而在一些统计和实际并不相符合的情况下，效率不一定比Merkle树高。

表6.1是3种方案的简单比较。

表6.1　三种方案的比较