Merkle Hash树也是一个Hash树，每一个叶子存放经过Hash后的散列码H（M），而根和内部节点的值都是它们孩子相连接后的Hash值。因为Hash树是二叉树，所以每一个父亲节点最多只能有两个孩子节点。具体构造Merkle Hash树时，首先每两个叶子节点相连接，然后进行单向Hash函数，生成的值就是它们的父亲节点，如此反复最后生成根。图6.5展示了构造Merkle Hash树的步骤。

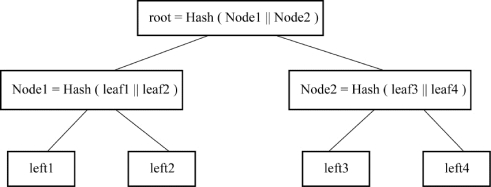
图6.5　Merkle Hash树

下面我们对Merkle树方法进行描述和分析。假设Alice的证书上仍然只有4个属性：姓名（Alice）、E-mail（Alice@163.com）、性别（女）、生日（1980-8-8）。然后进行如下步骤。

（1）首先生成4个随机数rv1、rv2、rv3、rv4，然后和每一个属性字段作连接并添加特殊标志符号“*”，这样就生成4个临时值tv1=Alice*rv1，tv2=Alice@163.com*rv2，tv3=女*rv3，tv4=1980-8-8*rv4，对这4个值Hash，生成4个叶子节点：leaf1=Hash（tv1），leaf2=Hash（tv2），leaf3=Hash（tv3），leaf4=Hash（tv4）。

（2）每两个叶子节点相连接，再Hash，生成中间节点node1、node2。node1=Hash（leaf1‖leaf2），node2=Hash（leaf3‖leaf4），符号“‖”表示前后两个值作连接，这里不需要添加特殊符号“*”。

（3）最后node1、node2相连接，再Hash生成root。root=Hash（node1‖node2）。

通过上述3个步骤产生了root，root将替换证书上的4个属性。(www.daowen.com)

如果Bob需要Alice出示姓名和E-mail，Alice需要发送tv1、tv2、node2。Bob通过下面几个步骤进行判别（符号“‖”表示前后两个值作连接）：

（1）计算leaf1′=Hash（tv1），leaf2′=Hash（tv2），node1′=Hash（leaf1′‖leaf2′）；

（2）计算root′=Hash（node1′‖node2）；

（3）比较root′和root，确认无误后，再通过特殊标志“*”从tv1、tv2中取得所需信息。

通过和原来的方案作比较，我们可以看到，使用现有方案需要在原始证书上存放每一个属性的散列值，这就要求证书有比较大的存储空间，而使用Merkle树，无论有多少个属性，证书上只需要存放最终的root就可以了。因为证书上面最终只展示root，所以用Merkle树极大地节约了证书的存储空间。

Merkle树方案实际是对已有方案的进一步扩展，因此完全可以实现数据的保密性、完整性、访问控制，也具有较高的性能。但使用Merkle树也有一定的不足，就是它的效率和现有方案相比有所下降。在原来的解决方案中，验证方需要什么信息，被验证方只需要发送相应的验证信息就可以了。而采用Merkle树方案，被验证方除了要发送相关的验证信息外（比如上面的tv1、tv2），还要发送一些无关信息（比如上面的node2），随着证书属性的增加，无关信息也就随着增加，这就增加了计算量，效率也就下降了。