秘密共享是将秘密分割成若干秘密份额，从秘密份额本身得不到任何关于秘密的信息，但是将一定数量即达到门限值的秘密份额放在一起就可以恢复秘密，而少于门限值的秘密份额联合起来无法恢复秘密。秘密共享是一种将秘密分割存储的密码技术，目的是阻止秘密过于集中，以达到分散风险和容忍入侵的目的，是信息安全和数据保密中的重要手段。

在秘密共享方案中，最常见的就是门限方案。门限方案是实现门限访问结构的秘密共享方案，在一个（m，n）门限方案中，m为门限值，秘密SK被拆分为n个份额的共享秘密，利用任意m（2≤m≤n）个或更多个共享份额就可以恢复秘密SK，而用任何m-1个或更少的共享份额是不能得到关于秘密SK的任何有用信息的。由于重构密钥需要m个共享份额，故暴露一个份额或多到m-1个份额都不会危及密钥，且少于m-1个用户不可能共谋得到密钥，同时若一个份额被丢失或损坏，还可恢复密钥（只要至少有m个有效的共享份额）。门限秘密共享可以避免单个用户腐败带来的安全隐患，使得密码系统既能保证足够的安全性，又能增强系统的稳健性。图3.1是（3，5）门限秘密共享方案。

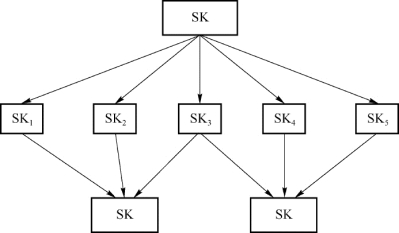
图3.1　（3，5）门限秘密共享方案

1979年Shamir提出一个称为（m，n）门限方案的构造方法。此方案是把一个信息（秘密的秘方、发射代码等）分成n部分，每个份额叫作它的“影子”或共享，它们中的任何m部分都能够用来重构消息，这就叫作（m，n）门限方案。

拉格朗日插值多项式方案是一种易于理解的秘密共享（m，n）门限方案。假定在n个人中共享密钥k，使得他们中任意m个人可以相互协作获取密钥。首先生成比k大的随机素数p。然后生成m-1个随机整数R1，R2，…，Rm-1，每一个都比p小。使用下列式子将F（x）定义成有限域上的多项式：

通过定义ki=F（xi）生成F的n个“影子”，这里每个xi都不同（如使用连续整数值[1，2，3，…，n]）。

将[p，xi，ki]交给n个秘密共享者的每一位，i对应每个共享者的号码。销毁R1，R2，…，Rm-1和k。

m个秘密共享者可以重构秘密。秘密共享者写出如下的线性方程。例如，号码为1的共享者可以构造方程：

(www.daowen.com)

这些线性方程有m个未知数C1，…，Cm-1和k，因此m个秘密共享者可以构造m个具有相同未知数的方程来求解（如使用消元法）。由于F的系数是随机选择的，所以少于m个秘密共享者的协作也不能解出k。

秘密共享解决了两个问题：一是若密钥偶然或有意地被暴露，整个系统就易受攻击；二是若密钥丢失或损坏，系统中的所有信息就不能用了。

n个参与者中的任意m个参与者出示他们的子秘密，从而得到m个点对：（x1，k1），（x2，k2），…，（xm，km），这样就可以重构多项式F（x）和共享的秘密k值如下：

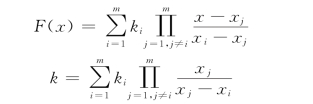
设秘密消息为M=11，我们构造（3，5）门限方案。随机选取正整数7和8，选取多项式F（x）=（7x2+8x+11）mod 13。计算5个影子分别为：k1=F（1）=7+8+11≡0（mod 13），k2=F（2）=28+16+11≡3（mod 13），k3=F（3）=63+24+11≡7（mod 13），k4=F（4）=112+32+11≡12（mod 13），k5=F（5）=175+40+11≡5（mod 13）。若已知k2、k3和k5，需要解线性方程：

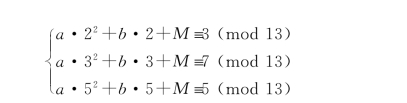
解是a=7，b=8，M=11。恢复出了秘密M。

在门限共享方案中，每个人拥有的影子份数也可以不同，拥有的份数越多，意味着权限越大。例如，某军事办公室由1名将军、2名上校和5名参谋组成。他们控制着一枚威力强大的导弹。他们不想发射导弹，除非将军决定发射，或者2个上校决定发射，或者5个参谋决定发射，或者1个上校和3个参谋决定发射。那么如何使用秘密共享方案实现此策略？设参谋持有的份额是x，则将军是5x，上校是2.5x。取整数x=2。总共份额至少是5x·1+2.5x·2+x·5=15x=30，故可以采用（10，30）门限秘密共享方案，将军拥有影子的份额是10份，上校每人5份，参谋每人2份。

可验证秘密共享是在通常的秘密共享方案中添加一个验证算法，这样份额持有者就能验证自己的份额与分发者分发的份额是否一致。Feldman将Shamir的方案改进为一个非交互的可验证秘密共享方案，在方案中，参与者之间不需要交互，且不需要存在可信第三方。方案如下。p是大素数，q是p-1的大素数因子，g∈Z*p且为q阶元。其中，参数（p，q，g）公开，3为门限值，n为参与者的个数，s为要共享的秘密。分发者从有限域GF（p）中随机选取2个元素a1和a2，构造二次多项式f（x）=s+a1 x+a2 x2 mod q共享秘密，计算子份额yi=f（i），并将子份额yi秘密地发送给参与者Pi，广播验证信息ga1 mod p和ga2 mod p，参与者Pi持有份额f（i），验证gf（i）=gs（ga1）i（ga2）i2确定持有的份额是否正确。