1.眼球模型

如图8.22所示，眼球是由大小不同的前后两个球面组成的。前面的小的部分约占眼球的1/6，为透明状，曲率半径约为8mm。后面较大的部分约占眼球的5/6，为不透明状，曲率半径约为12mm。眼球的前极点是透明部分（角膜）的曲率中心极点。眼球的后极点是不透明部分的中心后极点，它的位置略偏离于视觉神经位置，光轴就由这两个点定义而成。

定义小凹为视网膜中心，它是视网膜中最敏感和最发达的区域。因为小凹提供了最明显和最详细的信息，所以在观察物体时，眼球不停地旋转以保证观察物反射的光线能够落入这个区域。另外一个轴叫做视轴，它由通过节点O_cornea、小凹和观察物体连接而成。因此，视轴定义为用户的视觉注意点或视线方向。因为小凹略偏离眼球后极点，所以视轴略偏离于光轴。光轴和视轴在节点O_cornea形成的夹角叫做kappa，两只眼睛的角kappa大小一样，约为5°。

依据上面的眼球结构描述可以知道，眼睛的瞳孔3D轴线定义为瞳孔中心P和角膜曲率中心O_cornea的连线。又因为瞳孔轴线是估计眼睛光轴的最好方式，所以如果能得到瞳孔中心和角膜中心的三维位置，眼睛的光轴就可以估计得到。

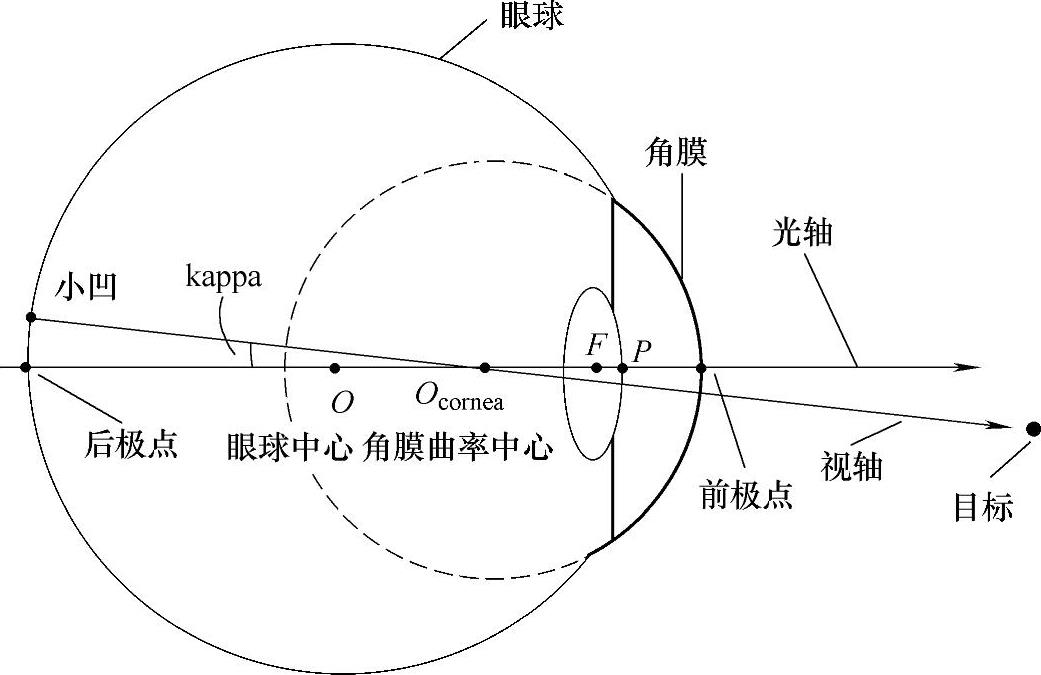
图8.22 眼球模型

2.3D角膜反射中心的计算

（1）普尔钦斑的形成

当光线通过眼睛时，角膜表面会成为一个反射表面。如果将一个光源放在眼睛前方，那么该光源所发出的光线在角膜的外表面将形成一个反射，在图像画面里的眼睛中会产生一个非常亮的点，这个亮点就是普尔钦斑。它是眼睛图像中最容易检测和追踪到的亮点。

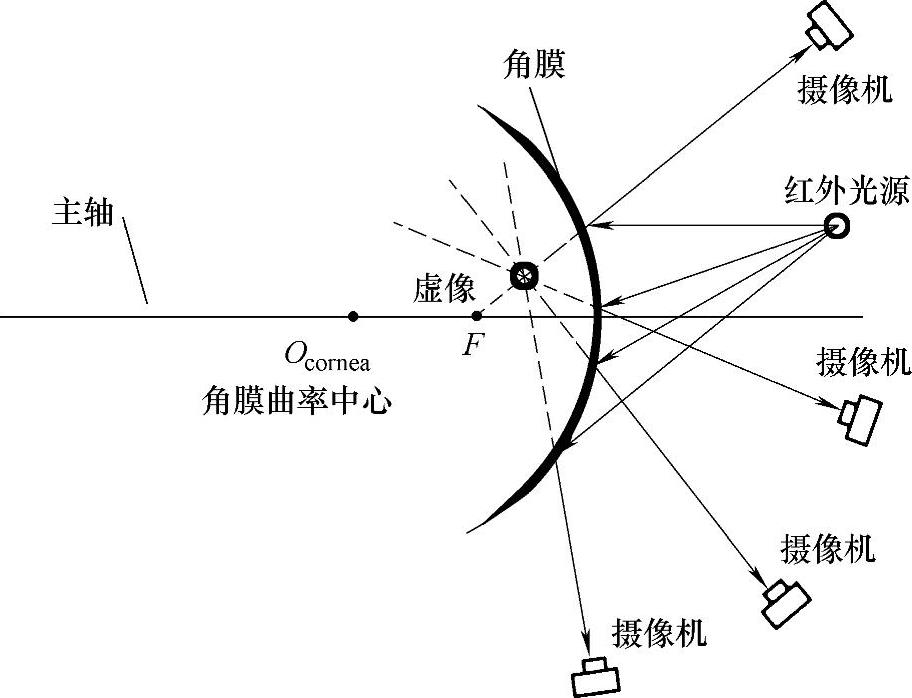
图8.23 将角膜作为球面镜时点光源在角膜中的成像

角膜的外表面可以假设为一个半径为R的凸透镜。因此，在普尔钦斑形成的过程中，眼睛的角膜扮演了凸透镜的作用。图8.23中定义了该凸透镜的焦距为F、曲率中心为O_cornea及主轴方向。在硬件系统中，使用红外Led作为光源。当红外Led放在眼睛前方时，会在角膜表面的后部，沿着连接角膜中心和光线的连线上产生一个红外光源虚图像，如图8.23所示。

如图8.23所示，光源的虚图像位于空间中的多个光线反射后延长线的交叉点。观察者从任何可视角度都可以看到以一个反射光点存在的虚光源。凸透镜的反射原理显示虚光源的位置只与光源的实际位置和透镜的位置有关，与观察者的位置无关。因此每个观察者不论在任何位置都可以看到同一位置上的虚图像。这样，定位红外光源虚图像的位置就是定位多个光线反射后延长线的交叉点。图8.23所示为几条光线从光源发出后到达角膜后被反射的过程。几条光线延长后相交于角膜后的一点，这个点就是所有光线延长后的交点，也就是虚图像的位置。

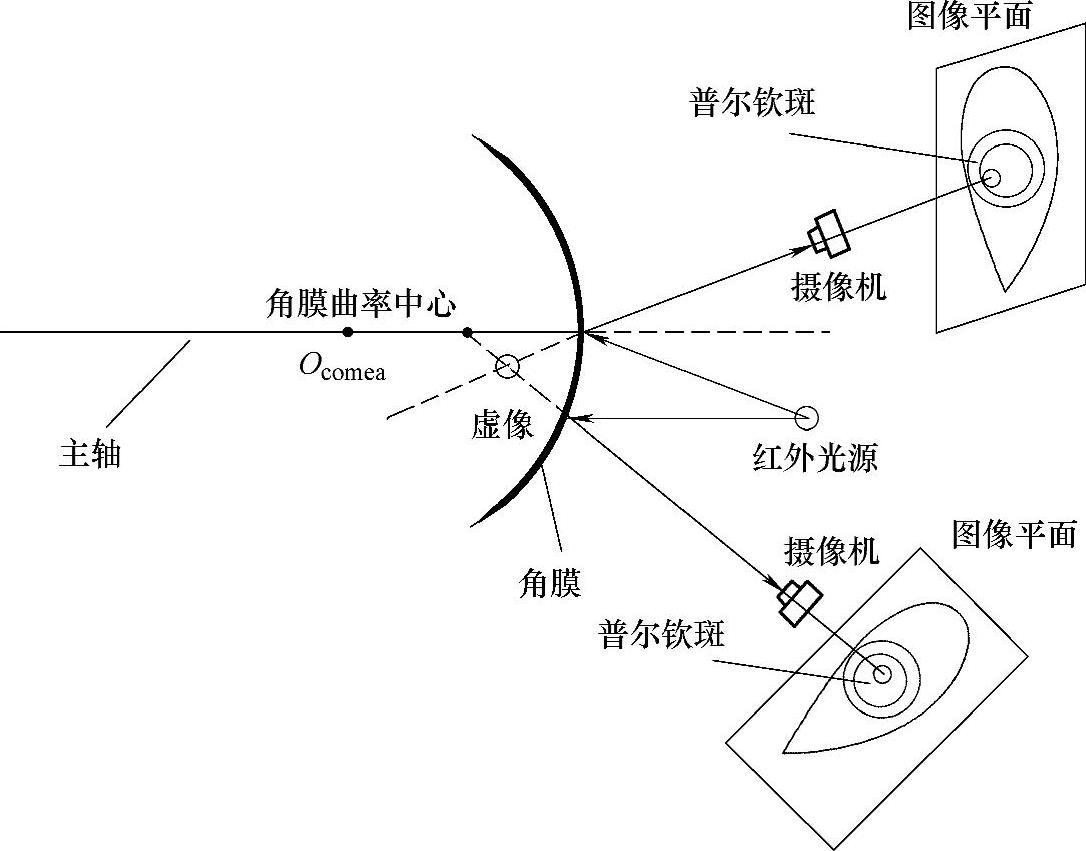
图8.24 红外点光源在角膜前的虚图像光线图

如图8.24所示，将摄像机作为观察者。红外光源在角膜上产生的虚图像被摄像机捕捉后就是所谓的普尔钦斑。如果把两台摄像机放在不同的位置，每台摄像机都会捕捉到在空间中由红外光源产生的同一个虚图像。因此基于机器视觉理论，使用两台摄像机就可以计算出由红外光源产生的虚图像的3D位置。

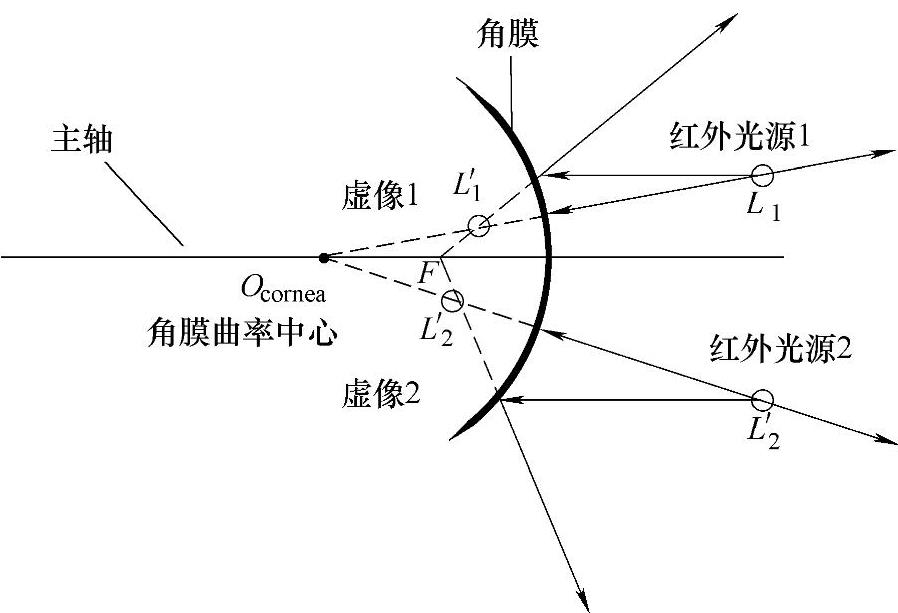
图8.25 两个红外光源在角膜前的光线图

（2）角膜的曲率中心

针对凸透镜的特性，当入射光线延凸透镜的曲率中心垂直入射时，光线会沿入射路线反射回去。因此，如果光线L₁L′₁垂直入射至角膜曲率中心，就会沿原路线返回，如图8.25所示。同样，光源虚图像L′₁会在这条路径上。因此，光源L₁、虚图像L′₁和角膜曲率中心O_cornea就是在同一条直线上。

进一步地说，如果在不同的位置再放一个光源L₂，那么光源L₂和它的虚图像L₂′及角膜曲率中心O_cornea就是在另一直线L₂L₂′O_cornea上。直线L2L2′O_cornea和直线L1L′₁O_cornea会交于Ocornea。

如上所述，如果使用两台摄像机组成立体视觉系统，红外虚图像L′₁和L₂′的空间位置就可以计算得到。而红外光源L₁和L₂的空间位置可以通过前述的环境标定过程得到。因此，角膜曲率中心的空间位置O_cornea可以通过L₁L′₁和L₂L₂′计算得到，公式如下：

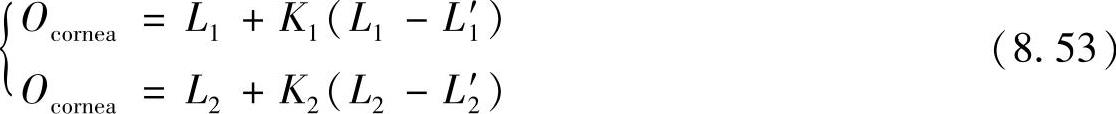(www.daowen.com)

当使用更多光源时，可以得到一系列的等式，这样可以在定位角膜中心时鲁棒性更好。

3.空间视线方向计算

（1）光轴估计

如上所述，由于瞳孔轴非常近似于光轴。因此，通过特征提取得到了瞳孔中心的3D空间位置后，眼睛的光轴V_P可以通过连接瞳孔中心空间位置P和角膜曲率中心O_cornea来得到。

V_P=O_cornea^+k（P-O_cornea） （8.54）

然而，由于角膜中溶液和外部空气的折射率不同，光线在眼球表面产生了折射，如图8.26所示。摄像机中观察到的实际上是瞳孔的虚图像，而不是真实的瞳孔本身。但是，因为假定瞳孔轴和眼睛的光轴极其近似，所以瞳孔中心位于光轴上。瞳孔的对称性使得瞳孔虚图像的中心仍然在光轴上，因此基于球面折射原理。图8.26所示的两条折射后的光线，仍然可以用来定位虚瞳孔的中心，这样虚瞳孔中心P′和角膜曲率中心就可以用来直接估计眼睛的光轴。

同理，由于虚瞳孔的位置独立于摄像机的位置，所以在给定的两幅图像中有同样的虚瞳孔。通过立体视觉空间三角测量就可以估计得到虚瞳孔的空间位置。由于眼球中央小凹在捕获的眼睛图像中不可见，眼睛的视轴也不能直接估计出来，这就导致注视点无法计算。但是眼睛视轴和光轴的偏差角kappa对每个人都是常数。角kappa可以通过用户个体标定得到。

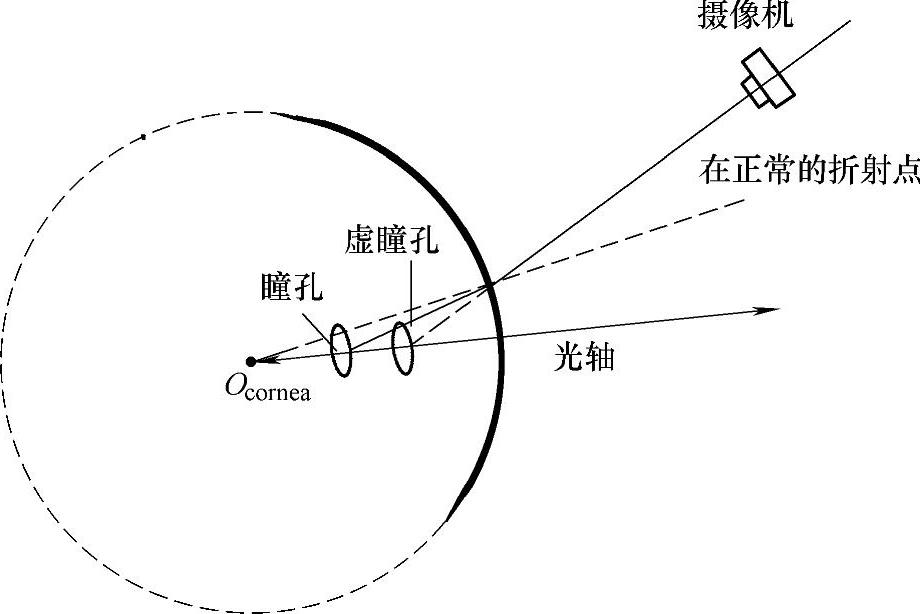
图8.26 在角膜和空气交界面发生折射的虚瞳孔光线图

设定一个关于眼球的三维空间坐标系统，Z轴是眼球的主轴，X轴是平行于三维空间水平面的轴。另外，在头部的左右和上下运动中，眼睛的X轴会始终与水平面平行。在头部的旋转运动时，眼睛会不自觉地沿着Z轴向头部旋转的反方向进行扭转，这样X轴仍能与水平面平行。但是眼睛只能扭转很小的角度。所以如果头部旋转的角度太大，眼睛的X轴就不能与水平面平行。

一般情况下，较大的头部旋转运动很少发生。因此在眼部运动中，可以认为眼睛的X轴会一直和水平面平行。这样如果偏差角kappa已知，那么视轴可以从估计的光轴中解出。

4.用户标定（偏离角kappa估计）

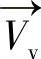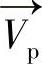用户标定的作用是对视轴和光轴偏差角进行补偿。当用户注视屏幕的已知点S时，这个点的空间坐标可以通过屏幕标定和坐标系转换得到。同理，角膜曲率中心O_cornea坐标、虚瞳孔中心坐标P′同样可以通过上述方法得到。因此，视轴方向和光轴方向可以通过下式得到：

另外，视轴和光轴的关系可表示为

这里M是3×3旋转矩阵，它代表了视轴和光轴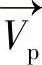之间的偏差关系。求得旋转矩阵M的值后，那么任意视轴的空间位置就可以通过检测到的相关光轴位置计算得到。因此，不用直接估计光轴和视轴偏差角kappa，通过标定旋转矩阵M就可以间接地求得光轴和视轴之间的关系。

旋转矩阵M可以通过一个简单的标定程序得到。在用户标定过程中，用户注视屏幕上k个预先设定的点S_i（i=1，2，…，k），一般k为9。标定后可以通过式（8.55）得到一系列矢量→V_v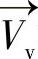和→V_p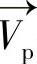。由于旋转矩阵M是标准正交的矩阵，所以公式可变为

因此，通过式（8.56）和式（8.57），一对矢量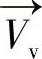和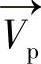就可以得到6个线性公式，那么2个屏幕点就足以估计3×3的旋转矩阵M了。如选择2个以上标定点，如上述的9个标定点，则可以通过最小二乘法求解矩阵M。

求得旋转矩阵M，眼睛的视轴就可以通过式（8.56）和光轴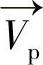得到。最终不同头部姿态下精确的注视点可以通过估计空间视轴和注视物体的交叉点检测得到。