基于非线性多项式和支持矢量回归的视线参数和视线屏幕落点之间的非线性映射模型结构如图8.9所示。

首先对采集到的平面视线参数进行标准瞳距补偿，然后将补偿后的平面视线参数输入到非线性多项式模型中，得到一个粗略的视线落点坐标；同时将头动相关视线参数输入到支持矢量回归模型，得到理想视线落点与多项式拟合视线落点的误差，用此误差对粗略视线落点进行补偿修正，得到最终的视线关注点坐标。

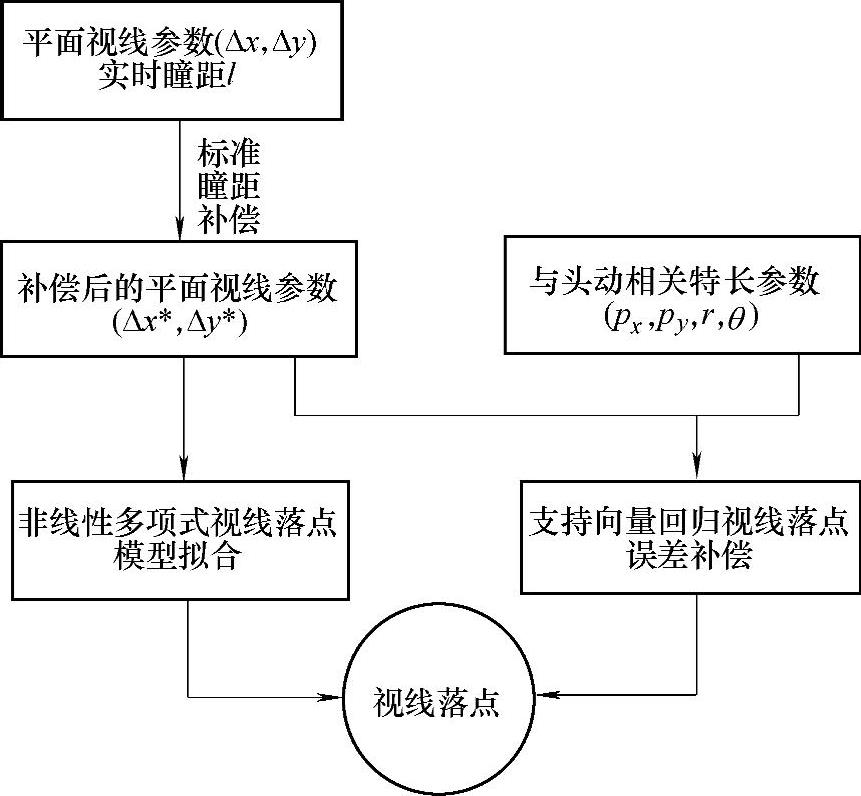
图8.9 二维视线模型结构

该方法旨在用单摄像机系统估计头动时的视线参数。另外，为补偿头部运动对视线方向的影响，需检测与头部姿态有关的眼睛特征参数。采集的人眼特征参数如下：瞳距l，用于瞳距补偿；拟合瞳孔椭圆的长短轴比率r，用来计算脸部转动偏移平面的大小；瞳孔椭圆的转动角度θ，用来计算脸部在平面内沿着视线轴方向转动大小；

（p_x，p_y）是瞳孔中心在图像中的坐标，用来反映人脸部的平移。

8.1.2.1 标准瞳距补偿

如图8.10所示，使用者的瞳距是固定值，但当使用者处于不同位置时，瞳距在图像上的像素值与用户距摄像机距离成反比。

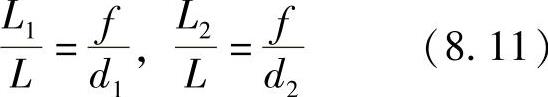
式中，f为焦距。可得。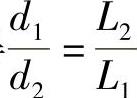

由式（8.11）可知，观测者与屏幕的距离变化会带来瞳距相应的变化，瞳距变化也会带来平面视线参数的变化。因此，选择标准瞳距对平面视线参数进行补偿可以减少由于头部与屏幕的距离远近而带来的估计误差。

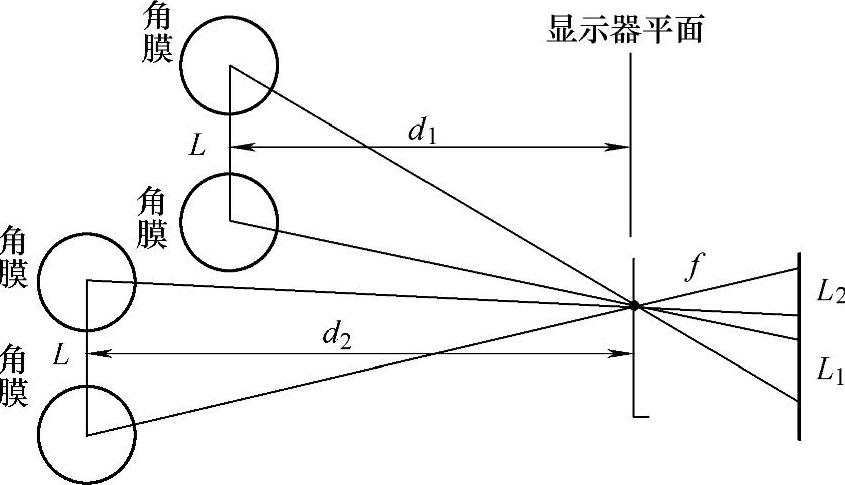
图8.10 瞳距与距离关系

8.1.2.2 非线性多项模型

头部不动的情况下，平面视线参数和视线落点之间的关系可采用如下多项式模型来拟合^[6]：

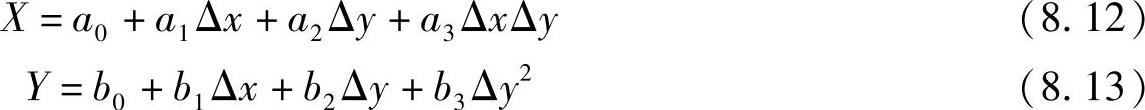
式中，X和Y为屏幕坐标的横坐标和纵坐标；系数a₀，a₁，a₂，a₃，b₀，b₁，b₂，b₃通过样本试验来确定；Δx和Δy为瞳孔普尔钦斑矢量的横坐标和纵坐标值。非线性多项式模型明确地给出了在头部静止情况下视线与瞳孔普尔钦斑矢量之间的映射关系。但是，在头部运动的时候必然使视线方向有所偏差，因此需要对上述模型进行一定的补偿。8.1.2.3 基于支持矢量回归的视线落点补偿模型

1.支持矢量回归训练

回归问题的目标是通过对样本的训练，找到一个函数f⊂F，使得在该函数下训练样本的值与其实际值的误差不大于给定的偏差。为叙述的方便，设函数有如下线性形式：

f（x）=（w，x）+b使得在该函数下训练样本的值与其实际值的误差不大于给定的偏差ε。作者采用的支持矢量回归（Support Vector Regression，SVR）的输入矢量为g=[Δx^*，Δy^*，r，θ，p_x，p_y]^T，即一组六维参数的输入矢量，输出矢量为非线性多项式拟合的视线落点与理想视线落点的水平和垂直方向的坐标误差，分别为d_x、d_y。

由于SVR一般是多输入单输出，因此对上述水平和垂直两个方向的输出分别建立一个数学模型。SVR模型选择包括：核函数选择，边际系数C的选择，损失函数的选择及与核有关的参数的选择等。采用交叉验证的方法来确定核函数的宽度σ和边际系数C，得出最优的核函数参数和边际系数。作者采用ε-支持矢量回归机^[18，19]，其模型构造按以下步骤进行：

1）设训练样本集为

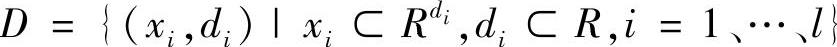
式中，x_i⊂R^di为测得的视线参数；d_i⊂R为在该参数下多项式拟合的视线落点与理想视线落点的误差。采集多人不同头部位置时的视线特征参数和视线落点偏差数据对SVM进行训练，一些典型头部位置如图8.4所示。在每个头部位置，被测试者分别注视屏幕上9个点，记录相关参数。将参数经过多项式模型映射后的视线落点与理想落点的偏差作为SVM目标输出，即期望输出^[20]。

2）选择高斯核函数为核函数，有

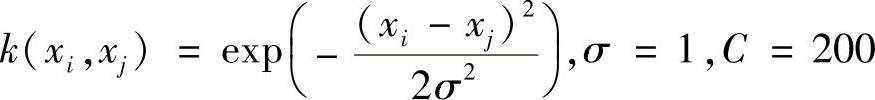
通过实验确定最佳的KKT条件终止精度ε=0.01，构造并求最优化问题：

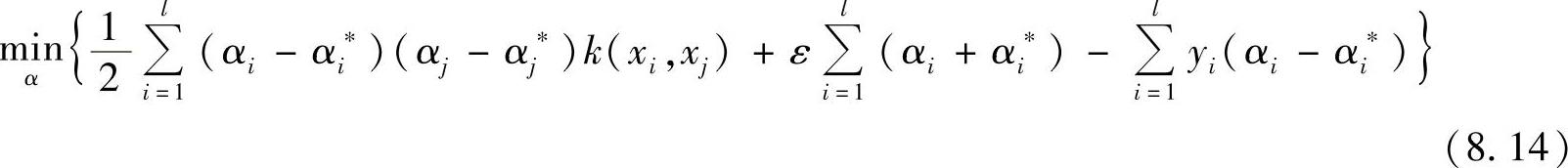
约束条件为

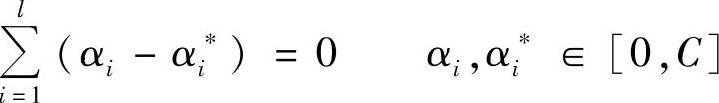(www.daowen.com)

3）解上述最优化问题得到拉格朗日乘子α_i、α_i*，构造回归函数为

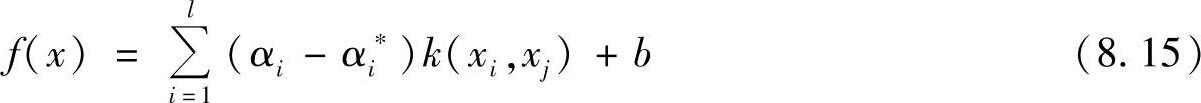
其中，偏置b按下式计算：

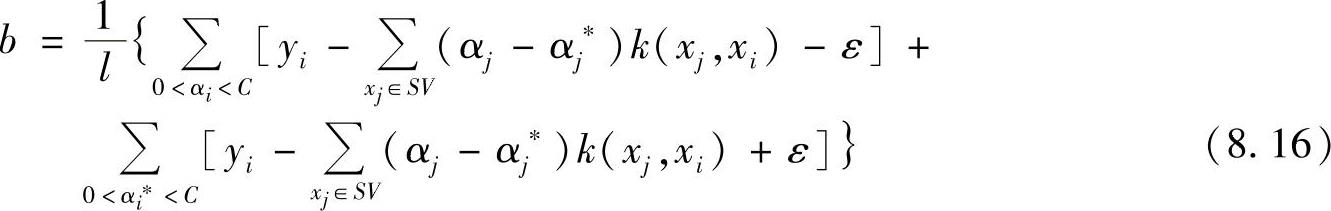
这样得到由输入矢量g描述的头部位置与视线估计误差（d_x，d_y）之间关系，即

d_x=f₁（g） （8.17）

d_y=f₂（g） （8.18）

训练过程只在建立模型时进行一次，以后使用系统时，可以直接使用f（g）对头部位置引起的视线落点误差进行补偿，无需重新进行训练过程。

2.基于SVM的头动补偿

训练完成后，支持矢量机（SVM）可以作为头动补偿函数。输入测量参数，将支持矢量机的输出作为补偿值，多项式拟合视线坐标与补偿值相加即为精确视线坐标。

8.1.2.4 实验结果与分析

1.参数提取与数据采集

系统训练和测试前，首先要进行参数提取，系统所用到的参数有平面视线参数（Δx，Δy）、瞳距l、拟合瞳孔椭圆的长短轴比率r、瞳孔椭圆转动方向θ、瞳孔在图像中的坐标位置（p_x，p_y）。采集数据阶段要求被测试者在一些典型头部位置如上仰、俯视、左偏、右偏等分别注视屏幕上的9个点，在每次注视过程中记录相应参数^[21]。

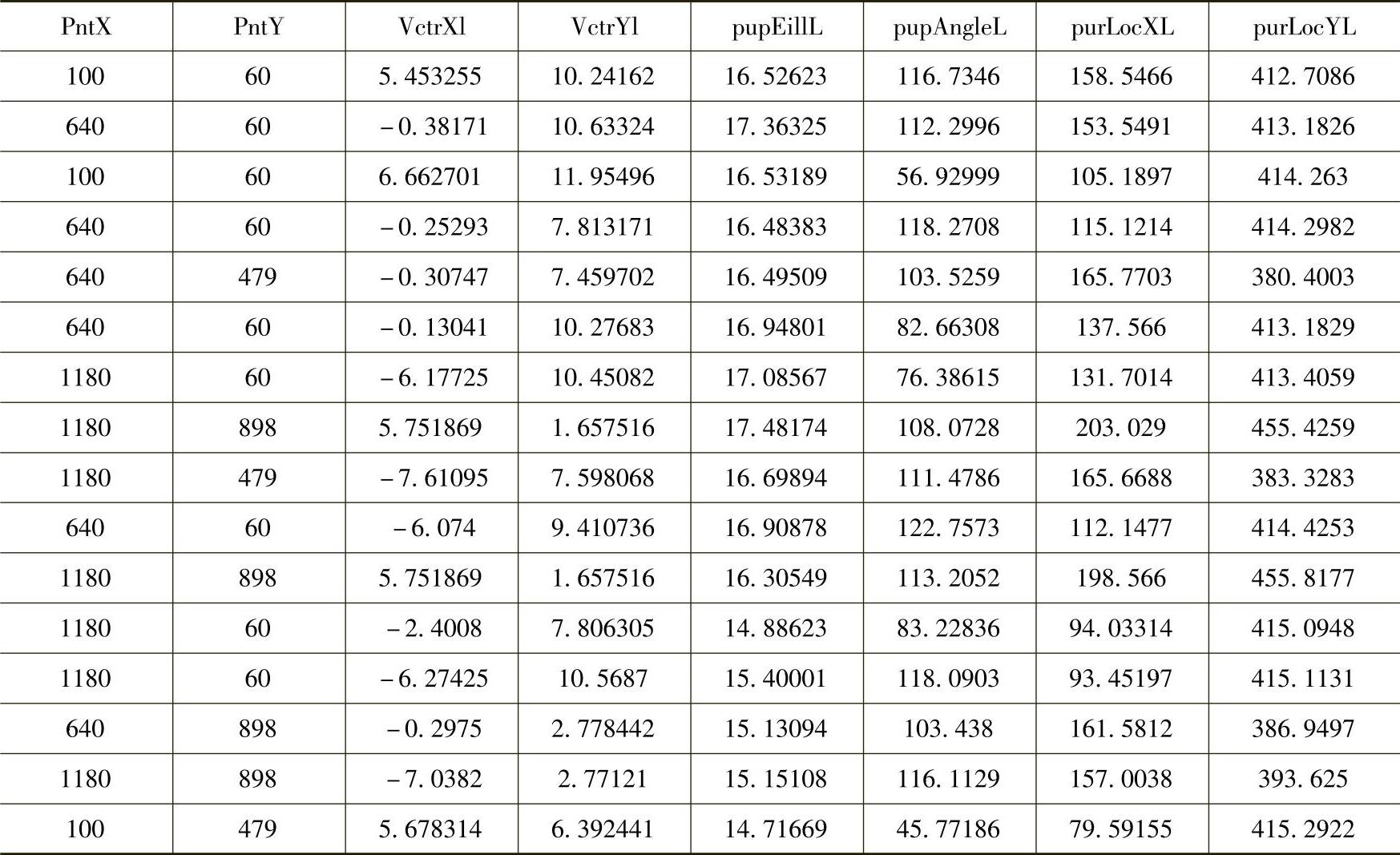
针对左右眼存在一定视差的问题，分别对左右眼进行参数采集，然后取双眼参数的平均值进行后续处理。实验采集的部分数据（左眼）见表8.2。表头的英文是计算程序中所命名的名字，对应的中文含义从左至右依次为注视点横坐标、注视点纵坐标、瞳孔角膜矢量横坐标、瞳孔角膜矢量纵坐标、瞳孔椭圆的长短轴比率、瞳孔椭圆的转动方向、瞳孔在图像中的横坐标与纵坐标。

表8.2 实验采集的部分数据

2.瞳距补偿前后估计结果对比

根据上述分析可知瞳距随着测试者与摄像机距离而变化，相应的平面视线参数也会发生变化。因此，采用标准瞳距补偿可以减少因为测试者与摄相机距离远近而带来的误差。

图8.11所示为部分测试点在瞳距补偿前后所产生的误差对比。随机选取部分数据制成条形图，其中每组左边的是补偿后产生的误差值，右边的是补偿前的误差值。实验结果表明补偿后的坐标误差小于补偿前坐标误差。

3.视线估计模型的效果

该方法用大量实验数据验证了经支持矢量回归补偿后的非线性多项式视线估计模型的效果（见表8.3）。大部分非线性多项式拟合后的结果在经过支持矢量回归机的补偿之后误差大大减少。这里的数据是不同的受试者经过训练之后得到的，因此对于相同的位置将得到不同的拟合值。

表8.3 改进后的二维视线估计模型的实验结果

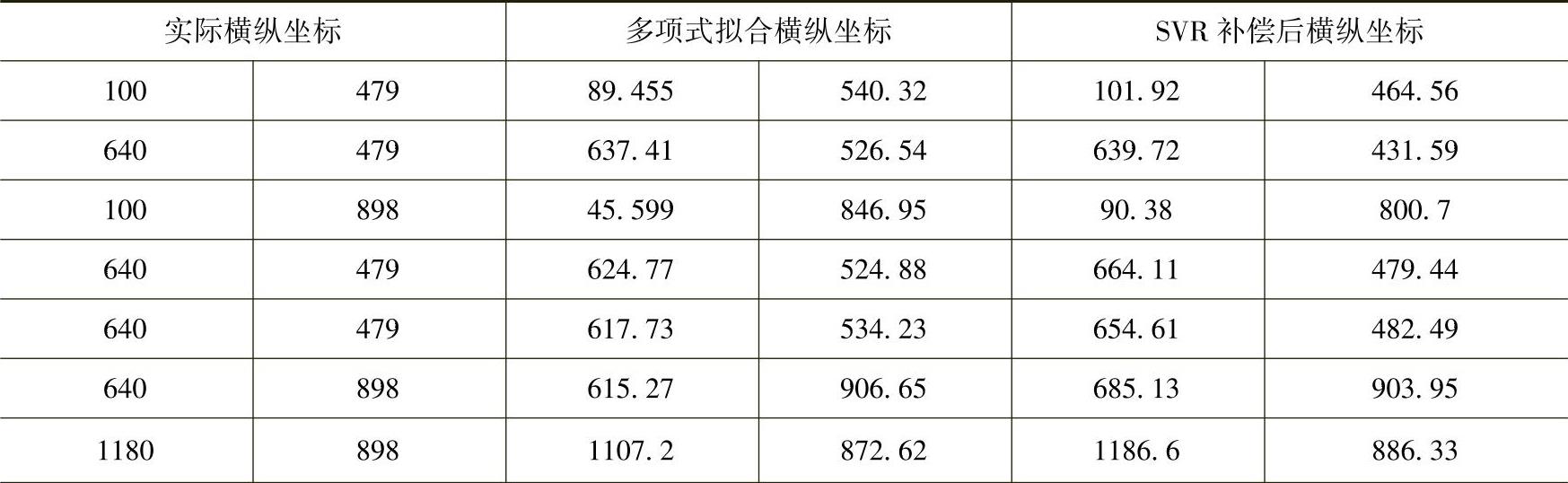
（续）

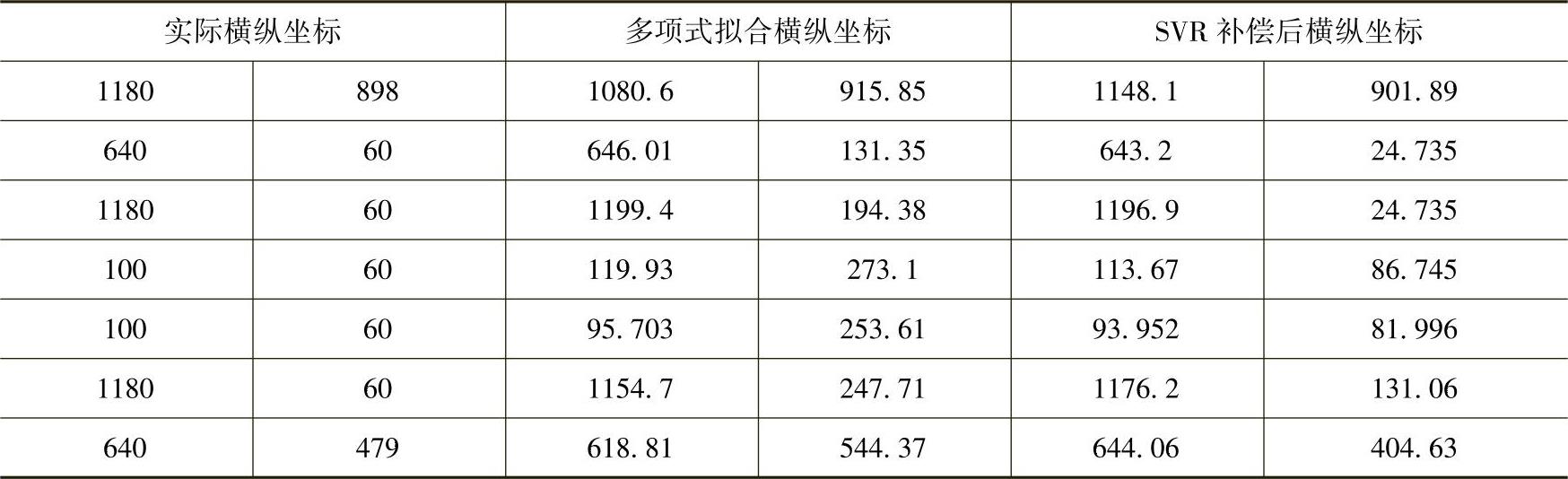
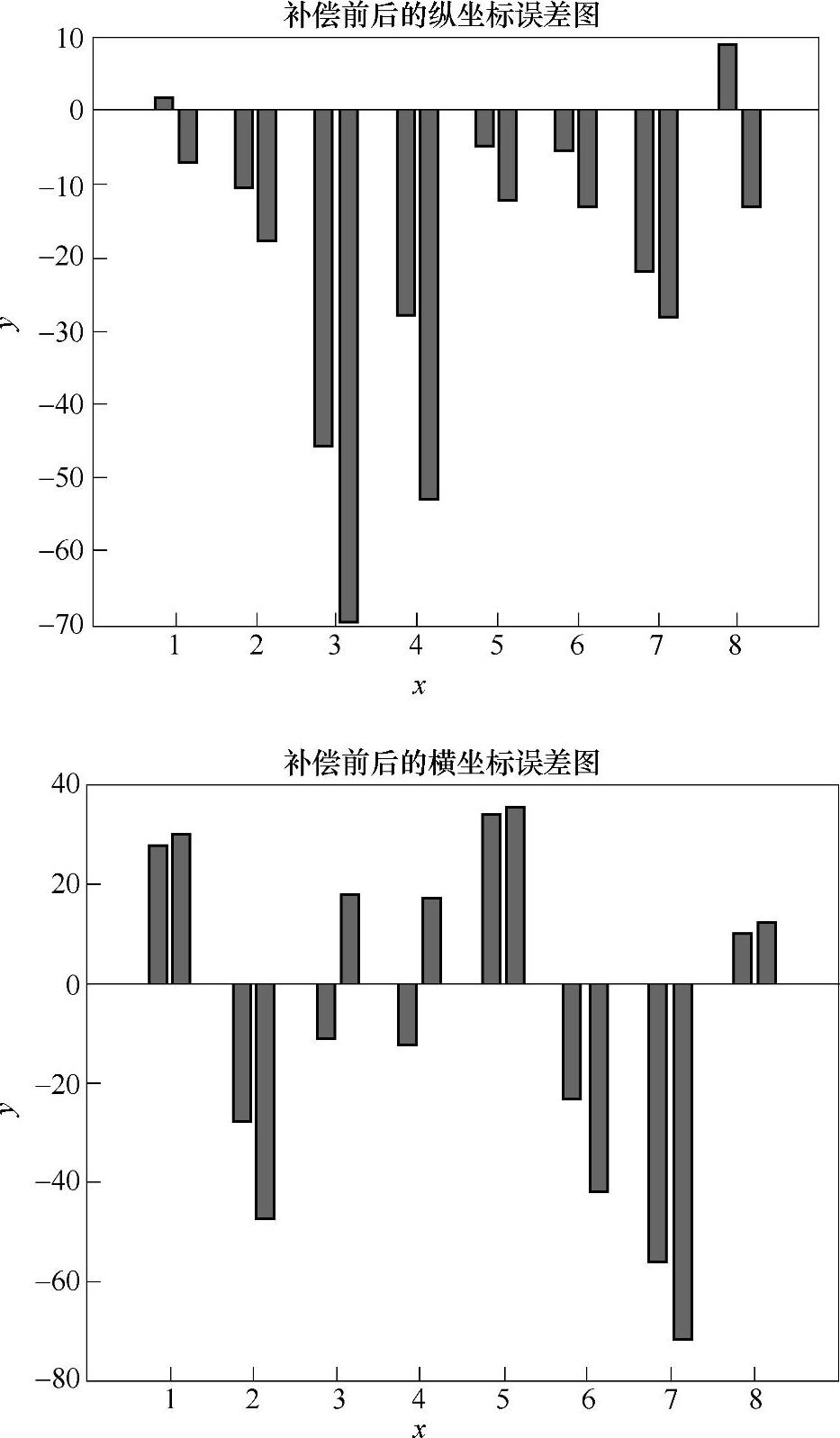
图8.11 标准瞳距补偿前后的横纵坐标误差对比

图8.12所示的图形更加直观地展示了基于非线性多项式和支持矢量回归的视线估计模型的估计效果。图中十字标注的是实际注视点，圆圈显示的是非线性多项式拟合后的盯视点，*显示的是经过支持矢量回归机补偿以后的注视点。图8.12表明经过支持矢量回归机补偿后的结果更加接近实际注视点。