8.1.1.1 广义回归神经网络

GRNN是基于概率密度函数的具有记忆功能的前馈神经网络。它训练快，能够有效逼近非线性函数，并且在噪声环境下也能很好地实现其功能。

GRNN的理论基础是非线性回归分析，非独立变量y相对于独立变量x的回归分析就是计算具有最大概率值的y。设随机变量x和y的联合概率密度函数为f（x，y），己知x的观测值为X，则y相对于X的回归，即条件均值为

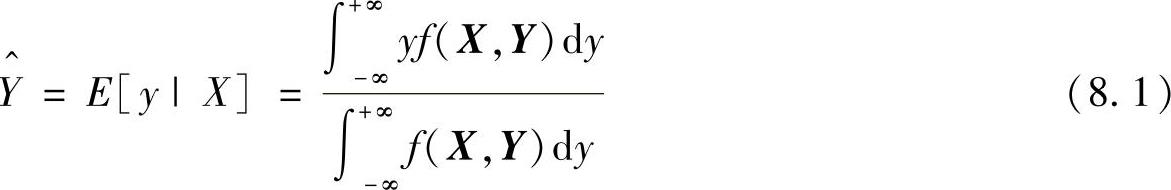
对于未知的概率密度函数f（x，y），可以由x和y的样本观测值估计得到其非参数估计为

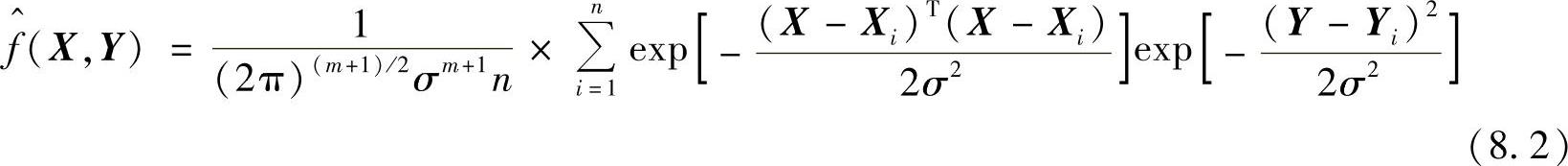
式中，X_i，Y_i为随机变量x和y的样本观测值；σ为平滑参数（核宽度）；n为样本数目；m为随机变量x的维数。用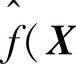，Y）代替f（X，Y），代入式（8.1）中，并交换积分与求和顺序，化简后有

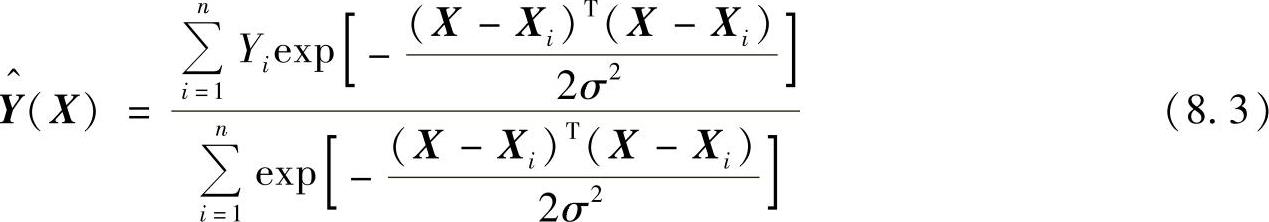
式（8.3）中，估计值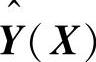为所有样本观测值Y_i的加权平均，每个观测值Y_i的权重因子是相应的样本X_i与X之间欧几里德（Euclid）距离平方的指数。

根据以上建立的GRNN由4层构成：输入层、隐含层、线性求和层及输出层。基于非线性多项式和GRNN的视线估计方法采用的基本结构如图8.1所示。

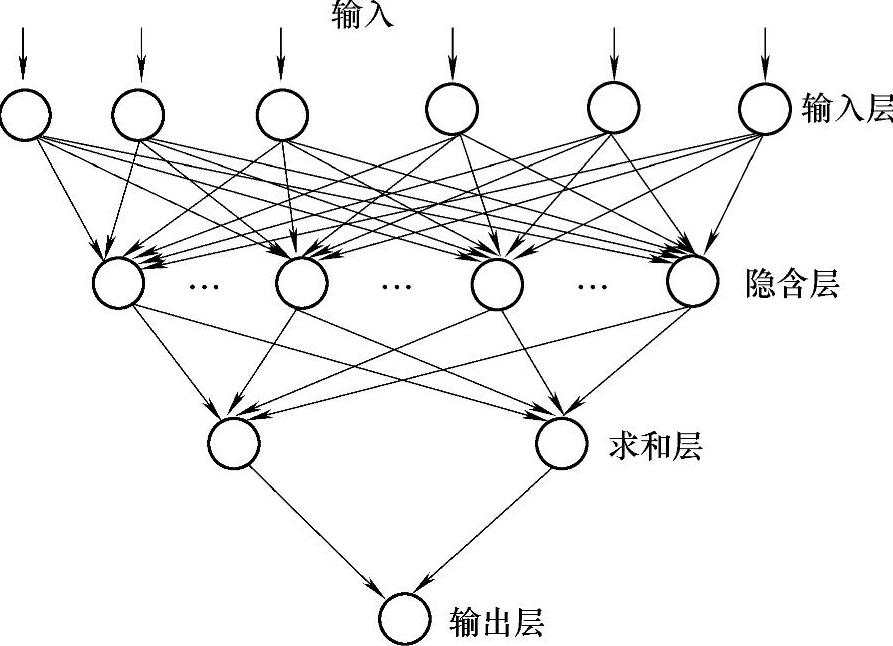
图8.1 GRNN结构

输入层中的神经元数目等于学习样本中输入矢量的维数m，各神经元是简单的分布单元，直接将输入变量传递给隐含层。隐含层的神经元数目等于学习样本的数目n，各神经元各自对应不同的样本，神经元i的传递函数为

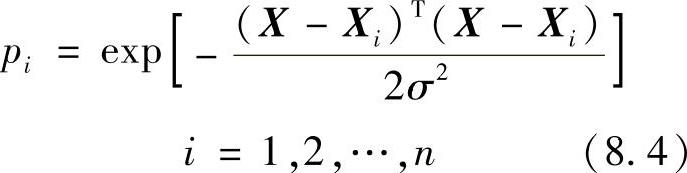
即神经元i的输出为输入变量X与其对应的样本X_i之间的Euclid距离二次方的指数形式。其中，X为网络输入变量，X_i为第i个神经元对应的学习样本。

求和层中使用两种类型神经元进行求和，一类相对式（8.3）中的分母部分，它对所有隐含层神经元的输出进行算术求和。隐含层连接权值为1，其传递函数为

S_D=∑P_i （8.5）另一类计算公式相对式（8.3）中的分子部分，它对所有模式层神经元的输出进行加权求和。隐含层中第i个神经元，求和层中第j个分子，求和神经元之间的连接权值为第i个输出样本Y_i中的j个元素y_ij。其传递函数为

输出层中的神经元数目等于学习样本中输出矢量的维数k，各神经元将求和层的输出相除，可得到式（8.4）的估计结果，神经元j的输出对应估计结果Y^（X）的第j个元素，即

8.1.1.2 基于非线性多项式拟合和GRNN的视线落点映射模型

1.与头动有关的眼部参数

实验研究表明，在前方摄像机摄取的人脸图像中，人脸的三维形态和瞳孔的形状（如瞳孔的大小、两眼瞳孔间距，外形、瞳孔椭圆具体位置等）具有如下规律：

1）人脸转移至正前方时，图像中瞳孔的间距将减小。

2）人脸转移至正前方时，左右两瞳孔之间的平均亮度会相差更大，一个更大一个更小。

3）人脸由正前方转移至其他方向时，瞳孔椭圆将变的更加扁。

4）当人脸朝向正前方并上下或左右看时，图像中的瞳孔都变小。

5）如果人脸绕着光轴旋转，瞳孔的相对位置也会改变。

基于上述研究并根据参考文献[3]的内容，采用头动状态下的视线特征矢量g，即

g=[Δx Δyaθg_xg_y]^T

式中，（Δx，Δy）为瞳孔中心到普尔钦斑的矢量；a为瞳孔椭圆长轴；θ为瞳孔椭圆长轴与垂直方向的角度；（g_x，g_y）为普尔钦斑在图像中的位置。（Δx，Δy）能够反映眼球方向及头部上下转动和左右转动，a能够反映头部与摄像机的距离变化，θ能够反映人脸绕摄像机光轴的转动，（g_x，g_y）能够反映人脸的平移运动。特征矢量g的变化可以充分反映头部和眼球的运动，为有效的视线方向估计及头动补偿提供了依据。

2.视线落点映射模型

该模型包括基于非线性多项式的视线拟合部分和GRNN的头动误差补偿部分，映射模型结构如图8.2所示。首先，在头部静止状态下，使受试者注视屏幕上的标定点，用标定多项式模型对视线的屏幕落点进行估计，然后不同的头部姿态下，注视屏幕上的标定点，计算对注视点的视线落点误差。同时，用经过训练的GRNN来计算头部运动引起的全屏视线估计误差。用估计的误差对视线进行补偿，得到最终的视线估计结果。

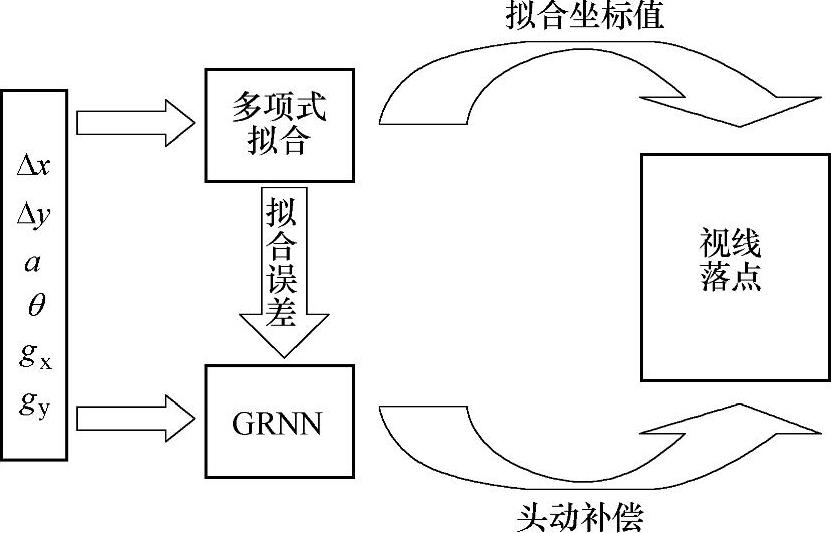
图8.2 映射模型结构(www.daowen.com)

（1）非线性多项式的视线落点直接拟合

平面视线参数和视线方向的关系很难用确定的解析式表示。但是在头部不动的情况下，人们做了大量的研究工作。即采用如下多项式来拟合视线[6]，可以取得较高的视线精度：

X=aΔx+bΔy+cΔxΔy （8.8）

Y=dΔx+eΔy+fΔx² （8.9）

式（8.8）拟合的是屏幕坐标的横坐标，式（8.9）拟合的是纵坐标。式中的系数a，b，c，d，e，f通过样本试验来确定。Δx和Δy为瞳孔中心-普尔钦斑矢量的横坐标和纵坐标值。这种拟合方式确定的视线方向为头部基本不动的情况下的视线方向。公式明确给出了在头部静止的情况下，视线与瞳孔中心-普尔钦斑矢量之间的对应关系。但是在头部运动时，必然使视线方向有所偏差，所以下面采用GRNN对其进行补偿。

（2）GRNN头动补偿

GRNN是径向基网络的一种特殊的形式，被广泛用于函数逼近。由于头部处于不同位置和姿态，这必然引起检测到的平面视线参数发生改变，即对视线的预测误差。而上节所叙述的视线计算方法并没有考虑到头动的影响，所以这里设计一个GRNN对头动的误差进行补偿。

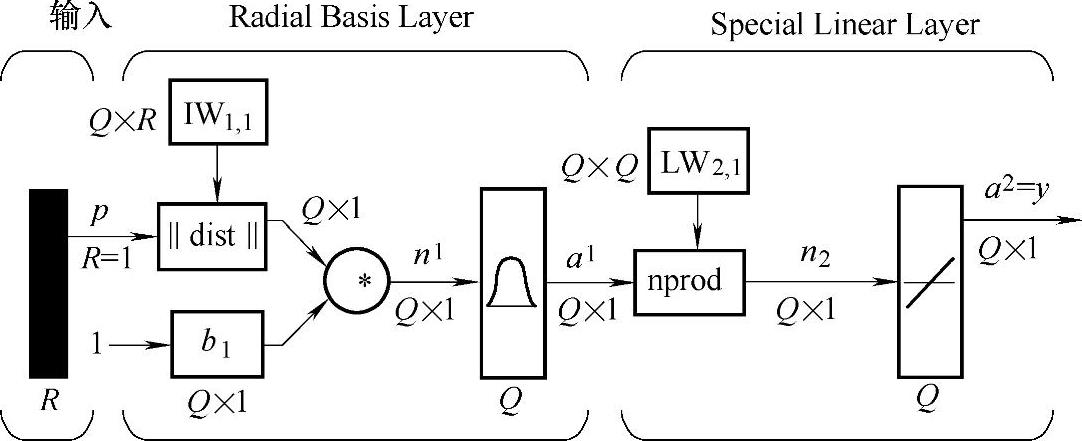
图8.3 GRNN模型结构

GRNN的一般模型结构如图8.3^[17]所示。图中的神经网络有Q组输入矢量，每组矢量的元素个数有R个。

对于GRNN，其初始化就是对训练样本的学习过程。这里在建立网络模型的时候，将网络学习样本中的输入矢量转置赋给图中IW；将训练样本中的目标矢量，即屏幕的坐标点赋值给LW。这样相应的网络结构和各神经元之间的连接权值随之确定。网络的训练实际上只是确定光滑因子的过程。与传统的误差反向传输算法不同，GRNN的学习算法在训练过程中无需调整神经元之间的连接权值，而是改变光滑因子，从而调整各单元的传递函数，以获得最佳回归估计结果。

令光滑因子以增量Δσ在一定范围（σ_min～σ_max）内递增变化。在学习样本中，留下一两个样本，用剩余的样本训练神经网络，然后对该一两个样本进行预测，得到预测值与样本之间的误差序列，误差序列的均方值为

将此作为网络性能的评价指标，将最小误差对应的光滑因子用于最后的GRNN进行预测。而式（8.10）即可作为网络训练的终止准则，光滑因子的确定过程隐含了网络性能的验证过程。

所设计的神经网络只有一个输出神经元，即只有一个输出。由于水平和垂直视线的显著区别，设计两个独立的GRNN，分别用来输出横、纵坐标的误差。然后，用误差与相应的拟合坐标值相加得到最后的视线坐标。输入的参数必须要反映不同的头部位姿和与摄像机的相对距离。这样才能够发挥网络的曲线拟合能力，找到参数与视线之间的内在规律，从而得到映射函数。神经网络的输入矢量为g=[Δx Δyaθg_xg_y]。在参数输入网络之前。对参数进行归一化处理，使参数在统一的数据范围内。

采集不同头部位置的数据对网络进行训练，一些典型的头部位置如图8.4所示。在每个头部位置，受试者分别注视屏幕上的9个点，记录相关参数。将参数经过多项式模型映射后的视线估计误差作为网络训练的目标输出，得到由输入矢量g描述的头部位置与视线估计误差之间的补偿关系，即

（ΔX，ΔY）=f_Δ（g）

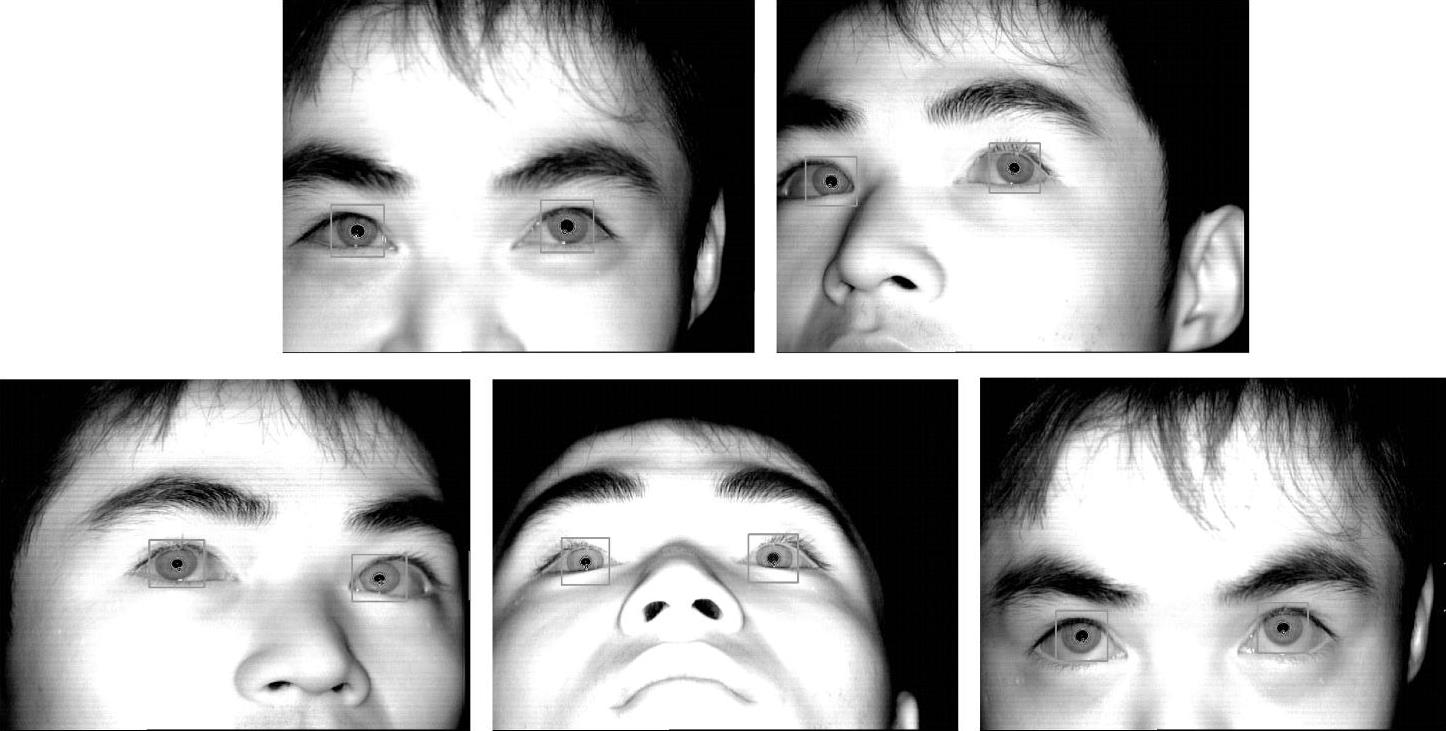
图8.4 一些典型的头动位置

这个训练过程只在建立模型的时候进行一次，以后使用系统时可以直接使用f_Δ对头部位置引起的误差进行补偿，无需重新进行训练过程。

8.1.1.3 实验结果与分析

为了验证基于非线性多项式和GRNN的视线落点估计方法的有效性，实验中收集了大量的实验数据对网络进行了训练并确定多项式模型参数。数据采集过程中，受试者分别注视屏幕上的9个点，记录相关参数。每个人都有头上仰、向下俯视、向左旋一定角度和向右旋一定角度等若干组数据。然后，测试每个人的头动误差，即将数据经过多项式拟合后的误差作为网络训练的目标矢量。

网络经训练好以后，给定一个输入矢量就可以确定一组误差（屏幕的横、纵坐标误差值），再加上多项式拟合的坐标，即得到修正的坐标值。这里取9个点对网络及整个系统进行了测试。将多项式直接拟合坐标与经神经网络修正后的屏幕坐标进行比较，屏幕坐标点头动补偿效果如图8.5所示。

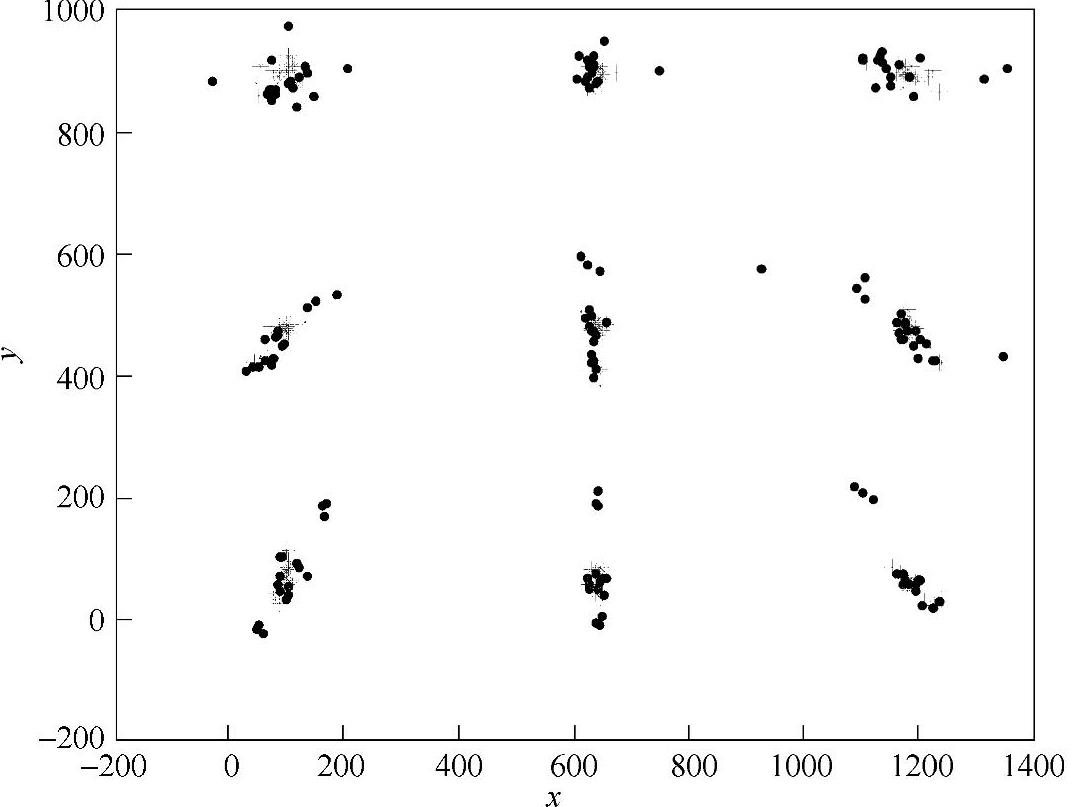
图8.5 屏幕坐标点头动补偿效果

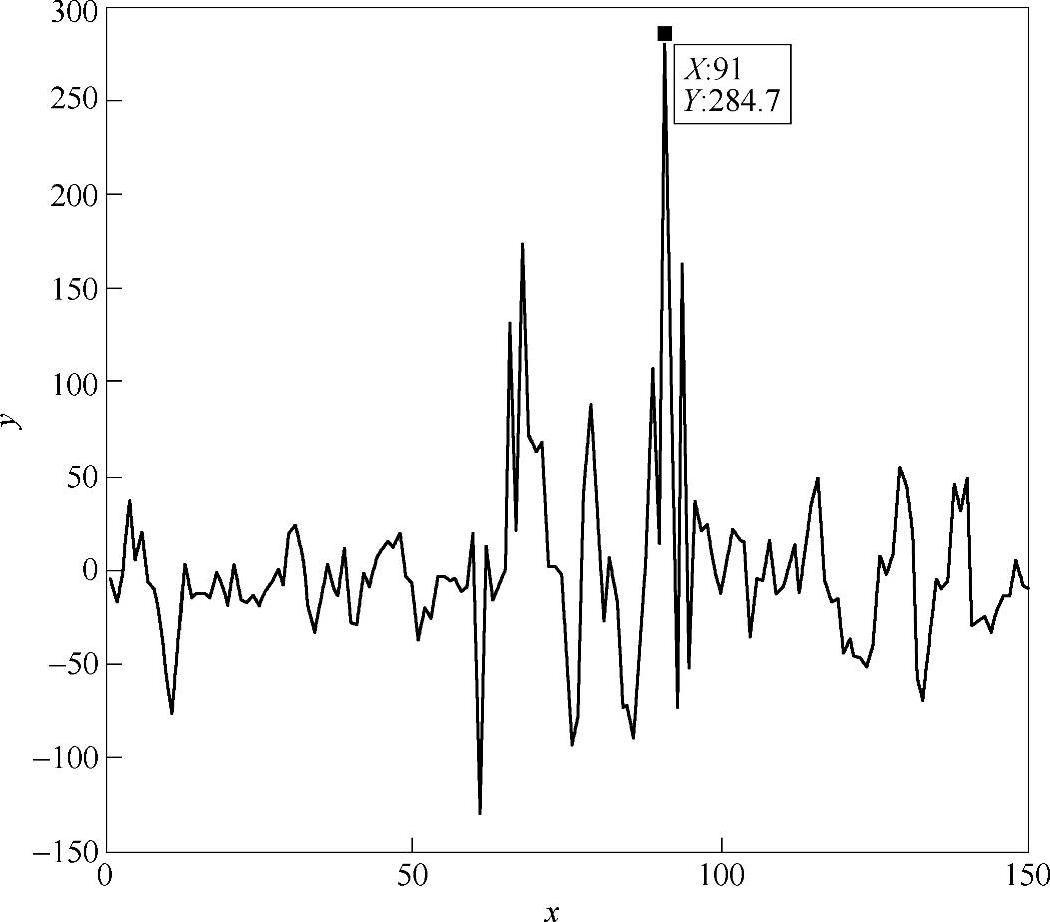
图8.6 由多项式直接拟合的x坐标误差图（纠正前）

显示屏幕上共9个点，所取数据包含用户正视正前方的数据及上下左右头动时的眼睛各个参数。头动的角度最大达到45°。图中，圆点表示根据用户的参数采用多项式直接拟合的屏幕坐标点，*表示经过神经网络的头动补偿后最后得到的坐标点。从图8.5可以直观看出神经网络输出对拟合精度的改善。图8.6和图8.7所示是以x坐标值为准分别给出来直接拟合和经过网络纠正后的视线落点坐标的映射误差。纠正之前，误差最大达284.7，而且大部分误差在50～100的范围内。而经过纠正以后（见图8.7），误差最大只有70个像素点，而且绝大部分的误差在20个像素点左右。这样不管是从单个像素点还是从总体上来说，都很大的改进了映射的性能。表8.1给出了一部分视线坐标补偿后的值，并给出补偿前拟合的坐标。同样可以看出，补偿后计算出来的视线精度更高。这种视线落点计算方法还在人机交互系统中得到了验证。通过眼睛的视线参数到视线落点拟合、补偿得到最终的视线落点坐标。这样在面向助老助残的数字家庭人机交互系统中就使用该方法。交互界面如图8.8所示。这种应用也证明了该方法的实用性。

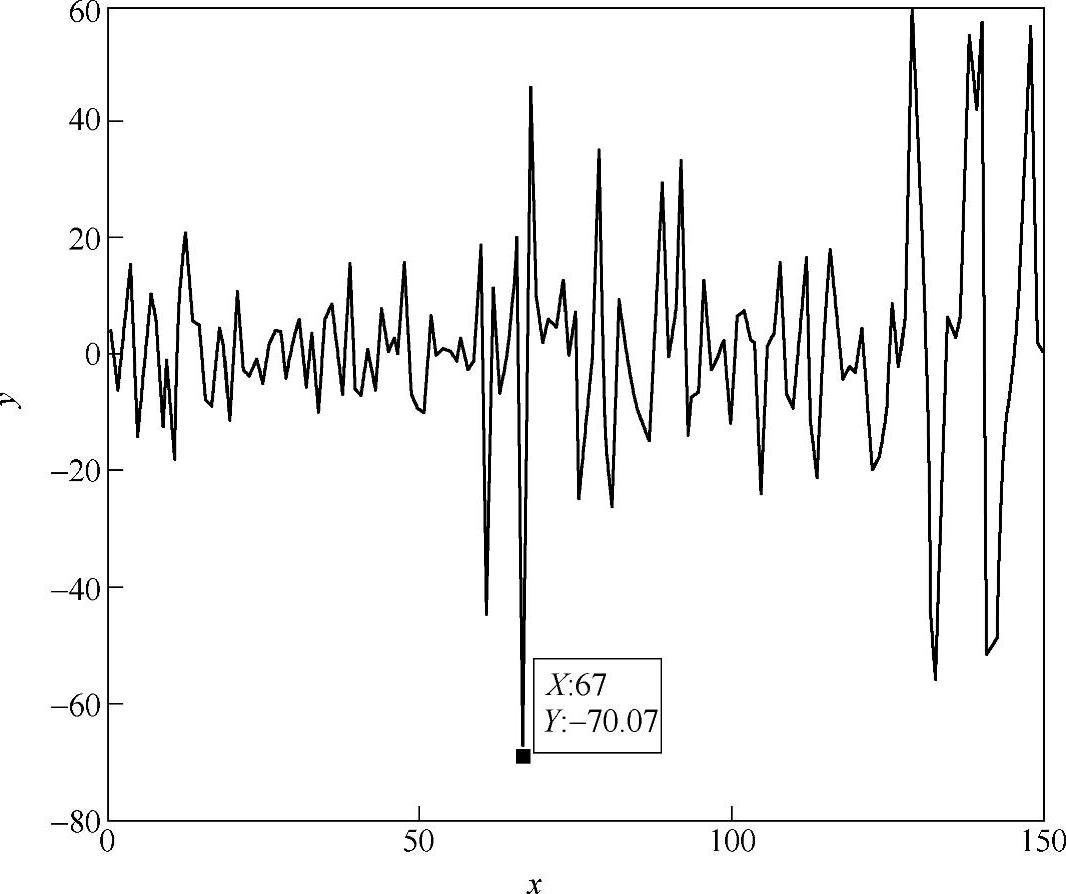
图8.7 网络纠正后的x坐标误差（纠正后）

表8.1 补偿后的视线坐标和直接拟合的视线坐标比较

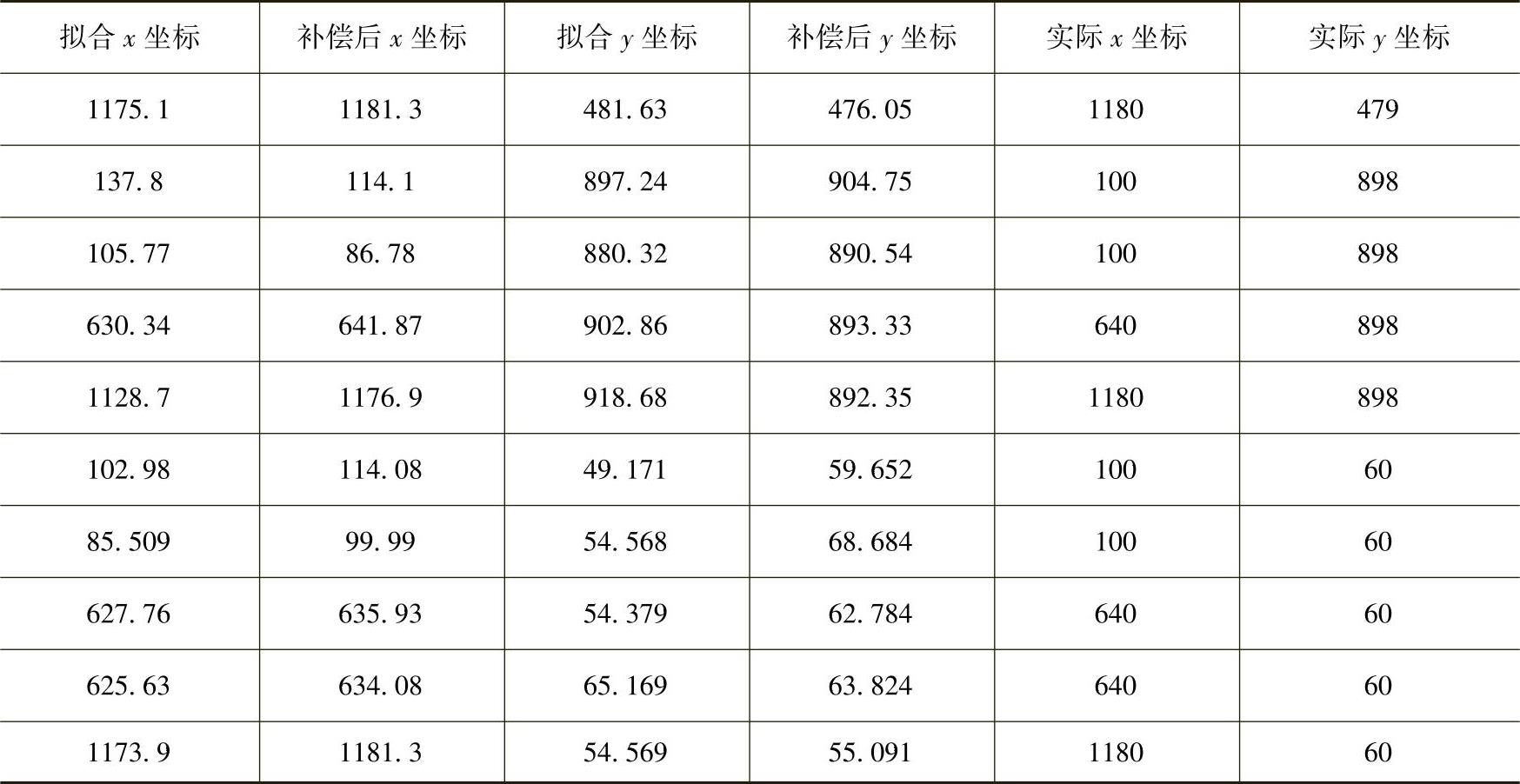
图8.8 人机交互界面