摄像机标定和双视觉系统标定后，在完成三维空间测量的基础上，通过标定摄像机组对系统摄像机不能直接拍摄的屏幕及光源进行标定。然后，通过全局标定确定系统摄像机和标定摄像机之间的关系。最后，通过坐标转换确定屏幕及光源在系统摄像机坐标系中的位置关系。

1.多摄像机坐标转换

标定系统中S组摄像机和G组摄像机的标定就是两系统之间的坐标转换问题[8]。三维空间中同一点P可用两个坐标矢量表示。一个是S组摄像机坐标系，即P_S=（x_Sy_Sz_S）^T；另一个是G组坐标系P_G=（x_Gy_Gz_G）T。P_S和P_G通常称为点P的同名矢量，它们在不同坐标系下描述相同点P。从S组摄像机到G组摄像机的坐标转换可以定义为

记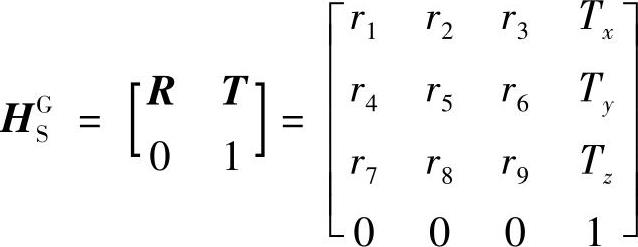

它为S组摄像机坐标系到G组摄像机坐标系转换矩阵。

目标靶是全局标定实现的必备条件，其作用是为各摄像机全局定位提供相应的标定控制点。本系统通过制定正反面完全对称的棋盘格目标靶将两组摄像机联系起来，以保证两组摄像机视野中观察到的三维点是在同一个坐标点。由四对以上同名矢量确定转换矩阵H^G_S，其求解实际上转化为最小二乘问题。建立目标函数[7]：

P～_G=（x_Gy_Gz_G1）^T、P～_S=（x_Sy_Sz_S1）^T分别为P_G和P_S的齐次坐标表示。式（7.56）中H^G_S的求解是线性的，且至少需要四对同名矢量。用多于四对的同名矢量可提高标定精度，此时H^G_S的解可用最小二乘线性回归求得

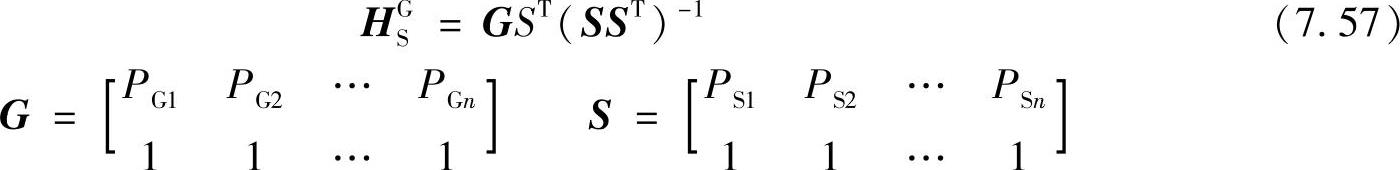
式中，n为标定点数，且n>4。

式（7.57）求得的转换矩阵H^G_S只是拟合标定点的最优解，但并不是确定两直角坐标系相互关系的最优解，因为H^G_S不满足正交约束条件。由此引入带有正交约束的最小二乘问题，即

将正交约束构造为如下函数：

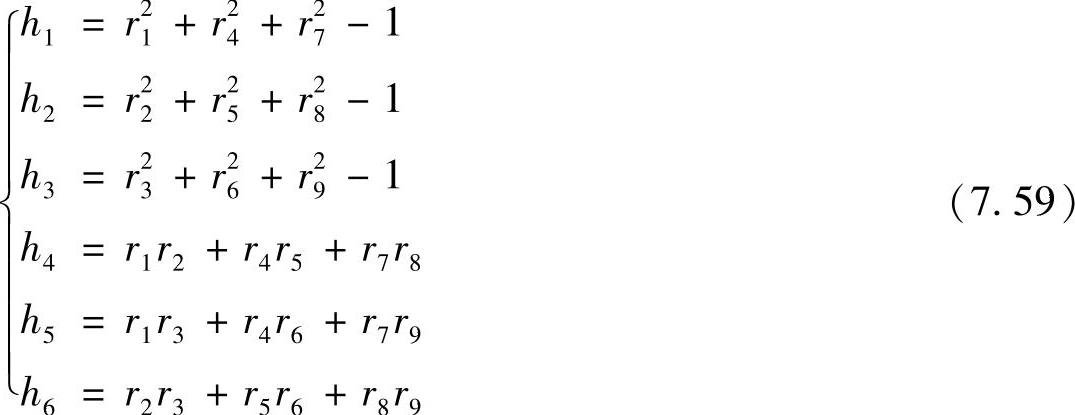
利用罚函数法将约束最优目标函数转化为无约束最优目标函数，即

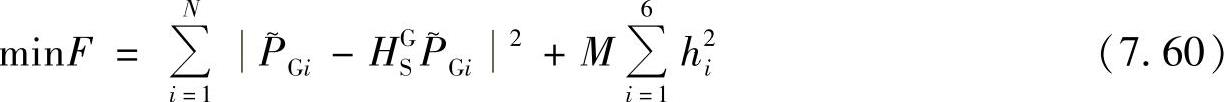
式中，M为罚因子，用于控制求解R矩阵正交性误差大小。约束条件的加入使得算法非线性，使用式（7.57）的线性算法确定的H_S^G作为式（7.60）的初值，然后进行快速非线性搜索，直至获得最佳的转换矩阵H^G_S。G组、S组坐标系中点的对应关系如图7.24所示。

图7.24 G、S组坐标系中点的对应关系图

2.显示屏幕标定

利用S组摄像机拍摄贴有标定模板的屏幕图像，如图所示。选取左右摄像机均能观测到的角点，利用Harris角点检测算法检测出所选角点的左右图像坐标，通过双视觉测量空间控制点的三维重建模型，计算得到屏幕上这些点在S组摄像机坐标系下的三维坐标。然后，通过多摄像机结构参数将之转换到G组摄像机坐标系下，这样便得到G组摄像机坐标系下显示屏幕上点的三维坐标。最后，利用多点平面拟合法求得显示屏幕所在平面的平面方程。

3.光源标定

光源标定是指测量出环形光源的环形中心在系统摄像机坐标系中的三维空间坐标。因此，对光源的标定类似于屏幕标定，即只要求出图像中光源所在圆的圆心坐标（即光源环中心的图像坐标）。这样，便可利用双视觉方法测量光源中心在S组摄像机坐标系下的三维坐标。首先，提取图像中光源所在的局部图像，如图7.26所示。图像中发光二极管与背景对比度很高，光源中心标定过程如下：

1）对图像进行预处理，得到二值化后的光源图像。(www.daowen.com)

2）对图像进行边缘检测。

2）利用广义Hough变换^[16-19]算法分别检测出左右摄像机所拍图像中每个光源所在的外环圆，并求出其中心坐标。

找出光源所在圆的中心之后，再对这些中心点的坐标利用最小二乘拟合方法画出所在椭圆，最后求出中心点坐标，这个坐标即为系统的光源中心点坐标。最小二乘拟合方法具体内容如下：

在二维的平面坐标系中，椭圆可用两种形式来表示^[19]。一种是利用圆锥曲线方程，即

Ax²+Bxy+Cy²+Dx+Ey+F=0 （7.61）

另一种是用平面坐标系的几何参数表示。设椭圆中心位置为（x_c，y_c），长轴和短轴分

图7.25 屏幕标定图

图7.26 光源中心坐标检测图

别为a、b，长轴的转角为θ。而二维平面里的任意一个椭圆都可以用这5个参数惟一地确定，参数的几何意义如图7.27所示。两种表示形式的参数可用式（7.62）～式（7.67）转换。

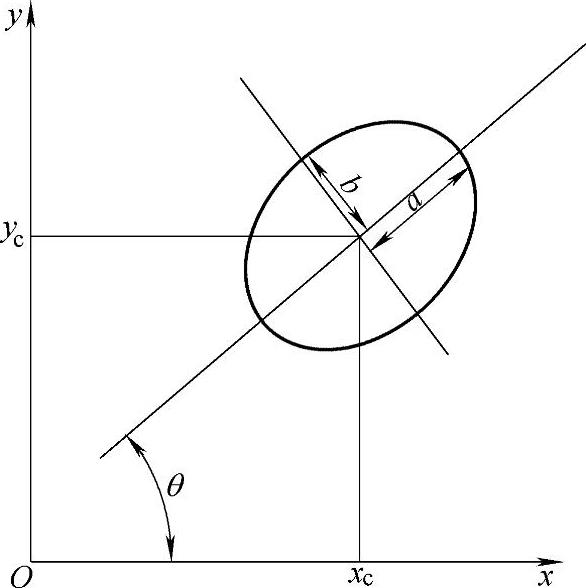
图7.27 二维平面椭圆的表示

最小二乘椭圆拟合法是一种较常用的椭圆拟合方法，通过寻找参数集合从而最小化数据点与椭圆之间的距离度量。距离度量常用几何距离和代数距离来表示。设平面内某点（x₀，y₀）到方程f（x，y）=0所代表曲线的代数距离是f（x₀，y₀）。以代数距离作为距离度量的最小二乘法介绍如下^[20]：

一般形式的椭圆方程如式（7.61）所示，为了避免方程零解，将解的任何整数倍都视为对同一椭圆的表述，对参数进行一些限制，并将约束条件设为A+C=1。因此，直接应用上述方程对边缘检测后的离散点进行最小二乘处理，就可以得到方程中的各系数。设目标函数为

图7.28 光源中心坐标检测图

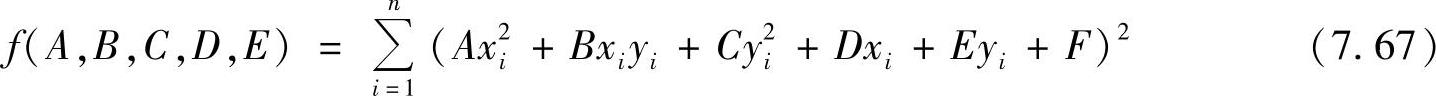
利用极值原理，使f（A，B，C，D，E）值为最小，则有

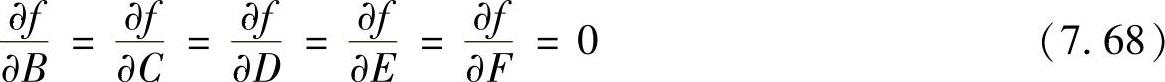
因此，可得一个线性方程组，然后结合约束条件，利用求解线性方程组的算法，就可以求得椭圆方程的各个系数A，B，C，D，E，F的值。

在已知椭圆方程的情况下，便可求得椭圆中心点的坐标，光源中心点检测图如图7.28所示。

在得到左右摄像机中光源中心点的左右图像坐标之后，再利用双视觉三维测量求出光源中心在S组坐标系下的三维空间坐标，最后将之转换到G组坐标系，即完成了系统的光源标定。