1.摄像机标定

空间某点的三维几何位置坐标与其在图像中对应点之间的相互关系，是由摄像机成像几何模型决定的。这些几何模型参数就是摄像机参数。多数情况下，这些参数必须通过实验与计算才能得到，这个过程称为摄像机的标定。标定过程就是确定摄像机的几何和光学参数，以及摄像机相对于世界坐标系的方位。

2.摄像机标定的目的

摄像机参数总是相对于某种几何成像模型的，这个模型是对光学成像过程的简化。如针孔成像模型，它是摄像机标定研究的基本模型。然而在很多情况下，这种线性模型不能准确地描述摄像机成像的几何关系，如在近距、广角的情况下。因此，还需考虑线性或非线性的畸变误差补偿后，才能更合理地将其看作针孔模型的成像过程，利用校正后的模型进行三维重建才能得到更高的精度。因此，成像模型和畸变误差补偿成为视觉中摄像机标定研究的重要内容。

摄像机标定实际上是要求出6个外参数R、T，5个内参数（f_u=f/S_x，f_v=f/S_y，u₀，v₀，μ），以及各种畸变系数k₁，k₂，p₁，p₂，s₁，s₂等。若不考虑离散后像素变形（不是矩形方块）或者成像平面不与光轴正交，则可以不考虑畸变因子_μ。一般情况下，畸变系数只考虑径向畸变系数，并设k₁=k₂=k。

如果已知摄像机的内外参数，即M矩阵已知，对任何空间点W，知道它的世界坐标（X，Y，Z，1）T，就可以求出其图像像素坐标系中该图像点w的坐标（u，v）。反过来，如果已知空间某点的图像坐标，即使已知内外参数，空间坐标也不是惟一确定的，它对应空间的一条射线。

3.经典摄像机标定方法

如图7.9所示，摄像机标定的基本方法：在一定的摄像机模型下，基于特定的实验条件如形状、尺寸等已知的标定参照物，经过图像处理，利用一系列数学变换和计算方法，求取摄像机模型的内部参数和外部参数。

经典的摄像机标定技术利用已知物体上的一些点的三维坐标和它们相应的图像点坐标，计算摄像机的内外参数。当前，对传统摄像机标定技术的研究集中在非线性畸变校正方面。

经典标定方法主要包括：透视变换法、张正友法、直接线性变换法、两步法和双平面法。直接线性变换方法是最优化算法的标定方法，两步法进一步考虑了畸变补偿，双平面法合理运用了摄像机的成像模型。

图7.9 摄像机标定示意图

经典标定方法具有标定精度高、可以使用任意摄像机模型的优点，其不足之处在于标定过程复杂，需要高精度的标定块或标定框架。在应用场合要求较高且摄像机参数不经常变化时，首选此类方法。

摄像机标定的张正友法^[21]

张正友的平面模板标定方法是介于传统标定方法和自标定方法之间的一种方法。它既避免了传统方法对设备要求高、操作繁琐等缺点，又较自标定方法的精度高。

根据摄像机成像模型，世界坐标点到理想像素点的齐次坐标变换如下：

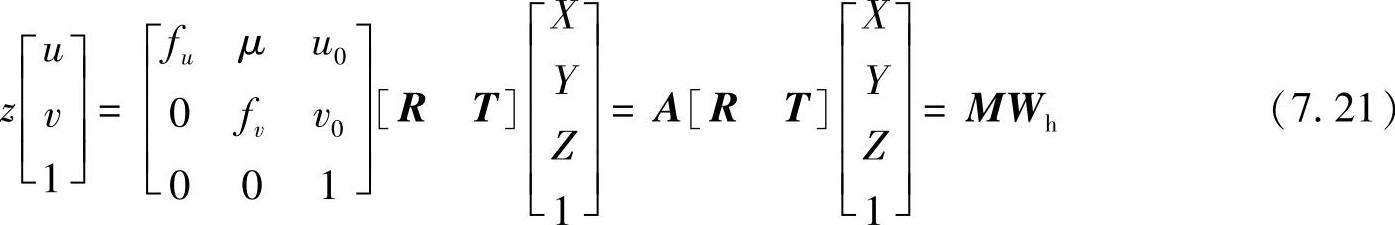
1.单应性矩阵的计算

为简化计算，取模板所在平面为世界坐标系的Z=0平面。用r_i表示R的第i列矢量。那么对于模板平面上的点有

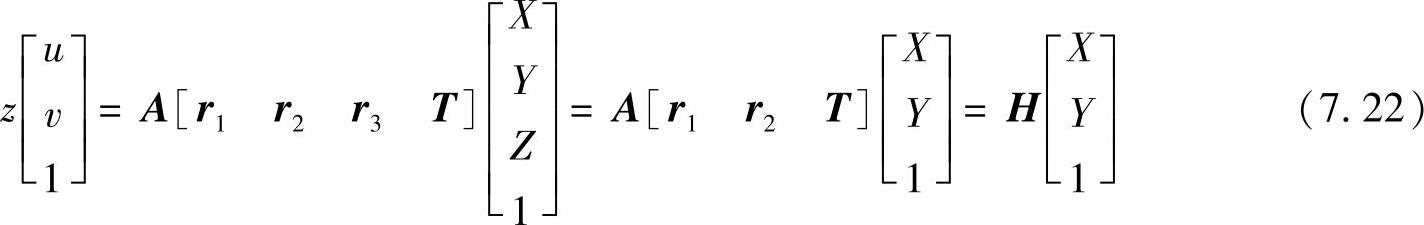
模板平面上的点和它的像点之间的映射由矩阵H=A[r₁r₁T]确定，这个矩阵称为单应性矩阵。设H

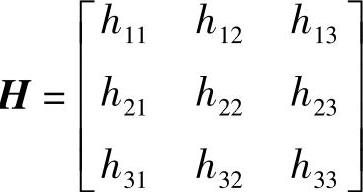
，可得

整理得

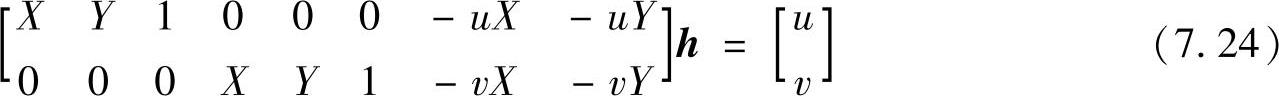
其中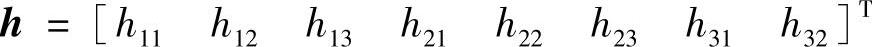

令H=[h₁h₂h₃]，则

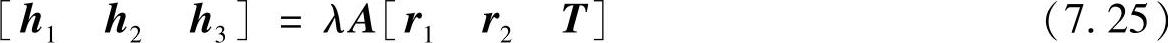
因为r₁和r₂是单位正交矢量，即r₁^Tr₁=r₂^Tr₂=1，且r₁^Tr₂=0，所以

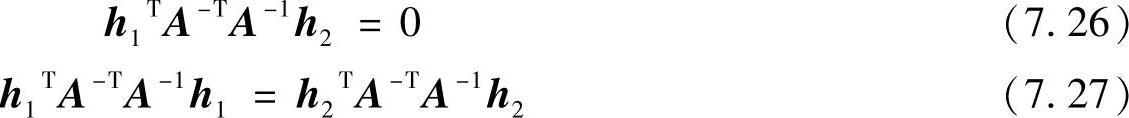
式（7.26）和式（7.27）为摄像机内部参数求解提供了两个约束条件。由于平面标定模板的单应性矩阵具有8个自由度，外部参数占了其中的6个（3个旋转和3个平移参数），因此只能利用剩下的2个约束条件。

2.参数求解(www.daowen.com)

令

可以看出，B为对称矩阵，定义6维矢量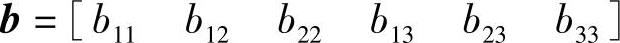，则有

式中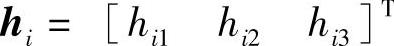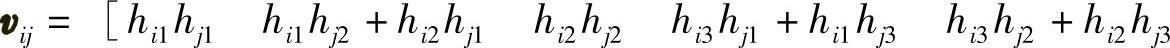，，h_i3h_j3]^T根据约束条件式（7.28）和式（7.29），可得关于矢量b的两个齐次方程，即

若有n幅平面模板图像，根据式（7.30），可得到线性方程组为

Vb=0 （7.31）

式中，V为一个2n×6的矩阵。如果n≥3，则可以列出6个以上的方程，从而解出一个带有比例因子的b。如果n=2，那么方程的个数少于未知数的个数。考虑到常用CCD传感器芯片都是方形，可以假定A中的坐标轴夹角为90°，即倾斜因子_μ=0，则有[01000 0]b=0，这就为式（7.31）提供了一个新的约束条件。如果n=1，需进一步假定摄像机的光学中心投影在图像的中心，方可解出。式（7.31）的最小二乘解为V^TV最小的特征值对应的特征矢量。

求得b即可获得矩阵B，根据式（7.28）可求得摄像机的各个内部参数，即

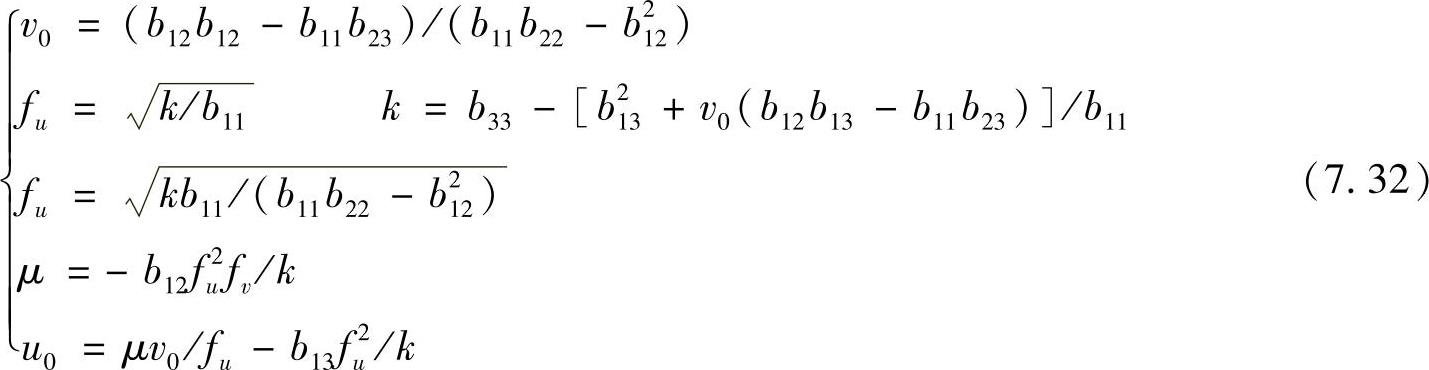
利用A和单应性矩阵H，对每个不同姿态的摄像机外参数可按如下公式求得：r₁=λA^-1h₁，r₂=λA^-1h₂，r₃=r₁r₂，T=λA^-1h₃，λ=1/‖A^-1h₁‖=1/‖A^-1h₂‖。

由于噪声的存在，R=[r₁r₂r₃]^一般不满足旋转矩阵的性质，这里采用最小距离准则来求R最优解。

3.最大似然估计

通过最小距离准则计算出的R的解在物理上没有意义，需要采用最大似然估计对结果进行精确求解。

设有n幅关于模板平面的图像，每幅图像中有m个标定点，每个标定点的数据都被独立同分布的噪声污染。建立目标函数如下：

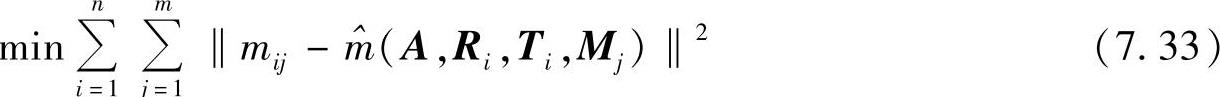
式中，m_ij为第i幅图像中第j个标定点的像点坐标；R_i、T_i分别为第i幅图像坐标系的旋转矩阵和平移矩阵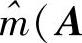，，R_i，Ti，Mj）是第i幅图像中的第j标定点的世界坐标的M_j通过式（7.22）求得的像点坐标。式（7.33）是典型的最小二乘问题，可以采用Levenberg-Marquar_- at算法求得稳定解。

4.径向畸变系数计算

上述标定过程没有考虑摄像机镜头畸变，实际摄像机镜头在远离图像中心较远处会产生较大的几何畸变。这里主要考虑一次和二次径向畸变，忽略其他畸变因素。摄像机镜头径向畸变模型为

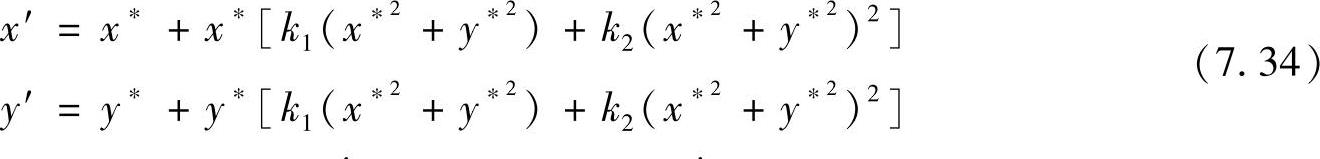
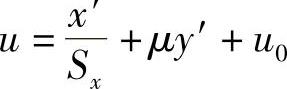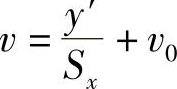根据像平面和图像坐标的转换关系和，可得

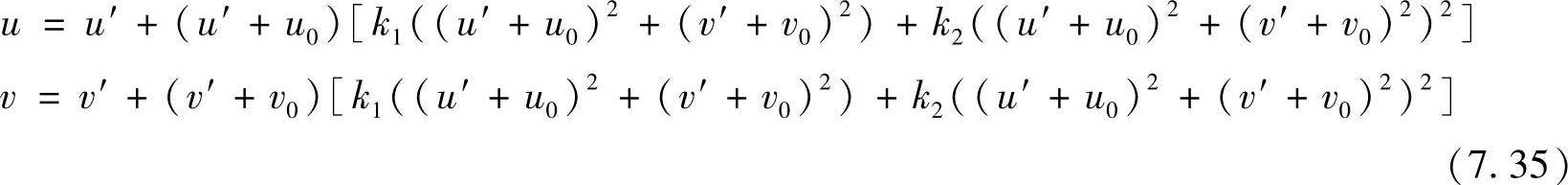
（u，v）为无畸变影响的理想的图像像素点坐标，（u′，v′）为图像实际像素点坐标。对上式整理得

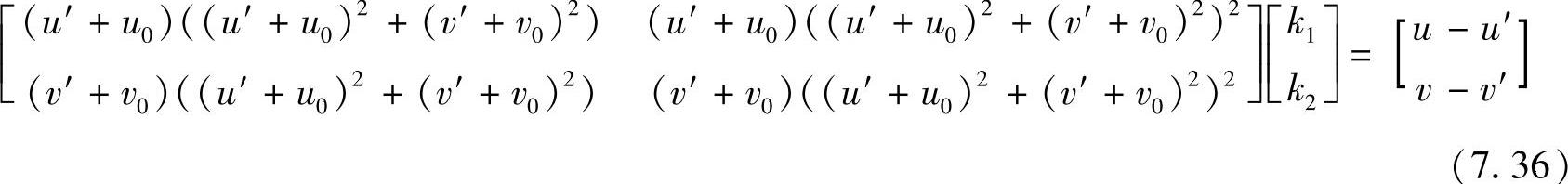
对于给定的n幅标定图像，每幅m个点，共mn个标定点，可以得到2mn个方程，用矩阵表示为

Dk=d （7.37）

式中，k=[k₁k₂]^T，式（6.118）的最小二乘解为

k=（D^TD）D^Td （7.38）

求得k₁，k₂后，采用前面类似的最大似然估计方法建立目标函数，即

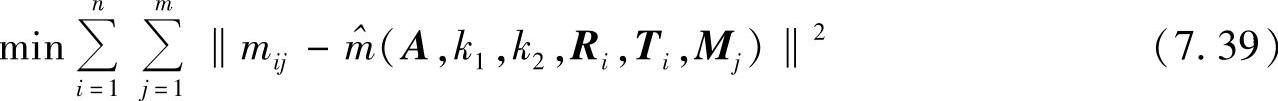
采用Levenberg-Marquarat算法求得最优解。