根据几个坐标系之间的相互关系，可以得到不同的成像几何模型，也称摄像机模型。

1.世界坐标与摄像机坐标重合时的摄像机模型

如图7.4所示，应用小孔成像模型，图像中摄像机坐标系统的xy平面与像平面重合，光学轴沿z轴。这样像平面的中心处于原点，镜头中心的坐标是（0，0，f），f是镜头的焦距。假设摄像机坐标系统与世界坐标系统XYZ平行。

设（X，Y，Z）是3D空间中任意点W的世界坐标。以下讨论都假设Z>f，即所有客观场景中感兴趣的点都在镜头前面。第一步要建立点W（X，Y，Z）与其投影到图像平面的坐标间的联系，借助相似三角形方便得到

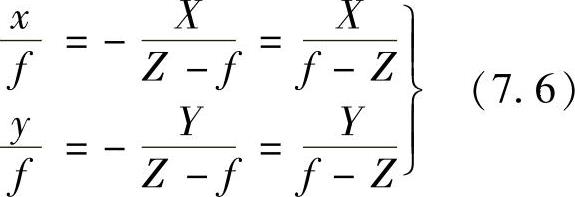
式中，分式前的负号代表图像像点反转。由式（7.6）可得到3D投影后的图像平面坐标，即

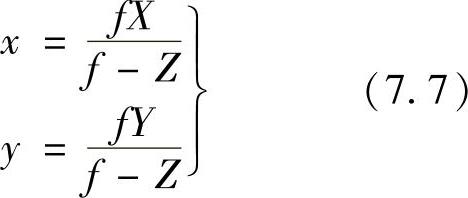
等式是非线性的，因为它们分母中含变量Z。可以借助齐次坐标将它们表示成线性矩阵的形式。

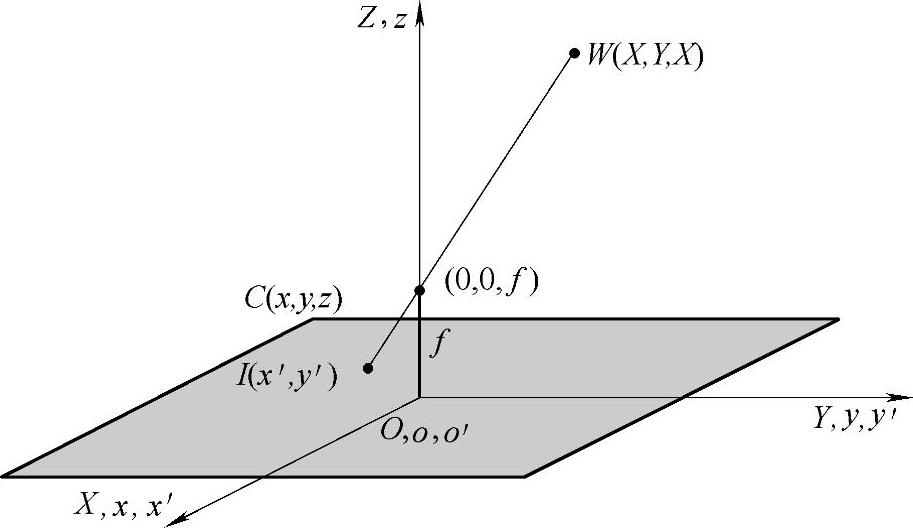
图7.4 投影成像示意图

空间一个点对应的笛卡尔坐标XYZ的齐次坐标定义为（kX，kY，kZ，k），其中k是任意非零常数。将齐次坐标变回笛卡尔坐标可用第4个坐标量去除前三个坐标量得到。这样一个笛卡尔坐标系统中的点可用矢量形式表示为

W=[XYZ]^T （7.8）

对应的齐次坐标可以表示为

W_h=[kXkYkZk]^T （7.9）

定义透视变换矩阵为

P和W_h的乘积给出了一个矢量，记为c_h，即

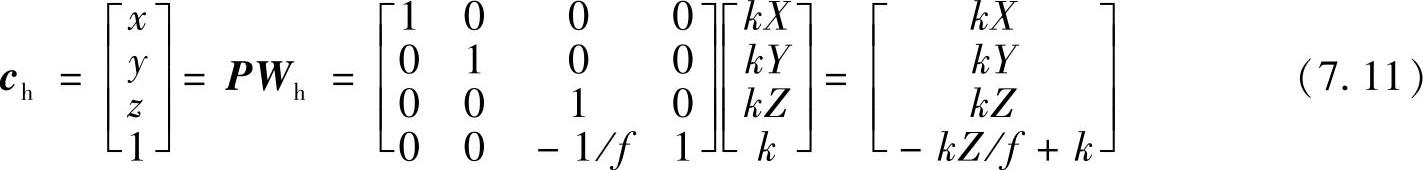
c_h的元素是齐次形式的摄像机坐标，这些坐标可用c_h的第4项分别去除前三项转换成笛卡尔形式。所以，摄像机坐标系中任意点笛卡儿坐标可表示成矢量形式为

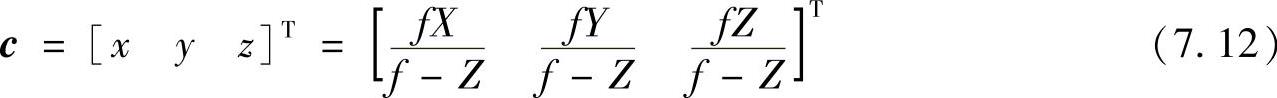
c的前两项是3D空间点（X，Y，Z）投影到图像平面后的坐标（x，y），第三项在图7.6所示的模型中无用，但逆投影变换中起自由变量的作用。

2.通用摄像机模型

通用摄像机模型要考虑如下一般情况：

1）世界坐标系、摄像机坐标系和像平面坐标系都不重合。

2）摄像机镜头的畸变误差，像平面上的成像位置与线性变换公式计算出的透视变换投影结果有偏差。

3）计算机中使用的图像坐标单位是存储器中离散像素的个数，所以像平面上的连续坐标还需取整转换。

图7.5所示为考虑上述因素时的通用几何模型示意图。图中，摄像机坐标系的原点o位于摄像机的镜头中心，像平面坐标中心o′位于光轴上，由小孔成像模型有oo′=f，f为焦距。从客观场景到数字图像的成像变换可看作由如图7.6所示的4个步骤组成。

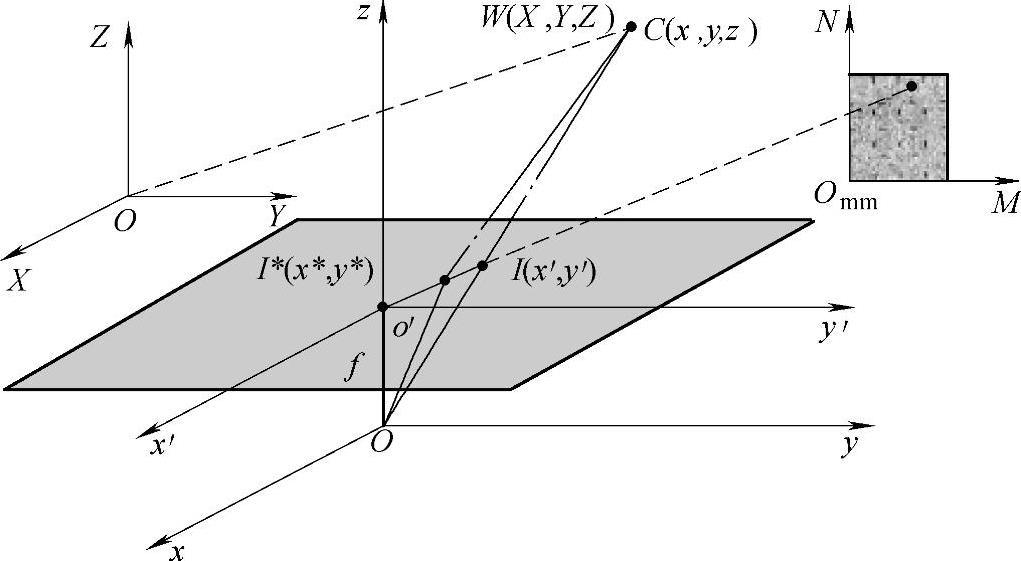
图7.5 通用摄像机模型示意图

（1）从世界坐标（X，Y，Z）到摄像机3D坐标（x，y，z）的变换

由前述摄像机模型可知，变换可表示为(www.daowen.com)

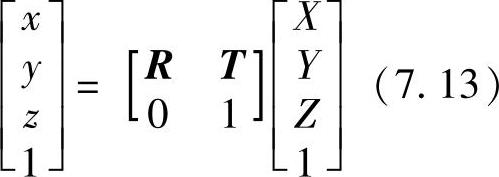
式中，R，T分别为3×3的旋转矩阵（两坐标系三组对应坐标轴间夹角的函数）和1×3的平移矢量。

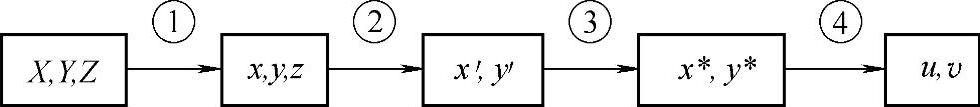
图7.6 从客观场景到数字图像的成像变换步骤

（2）从摄像机3D坐标（x，y，z）到无失真像平面理想坐标（x′，y′）之间的变换

将上式用齐次坐标形式与矩阵表示为

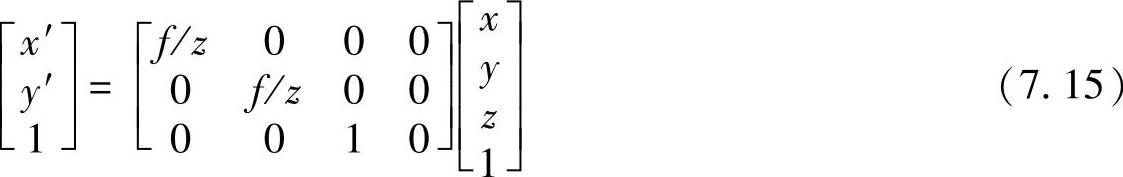
（3）从无失真像平面理想坐标（x′，y′）到受镜头畸变影响而偏移的实际像平面坐标（x^*，y^*）的变换

三者关系为

式中，δ_x*，δ_y*为镜头畸变。

（4）图像坐标（u，v）与像平面坐标（x′，y′）的变换

1）图像坐标系。采集的数字图像在计算机内可以存储为数组，数组中每一个元素为像素。在图像上定义直角坐标系uv，每一像素坐标分别是该像素在数组中的行数和列数。所以（u，v）是以像素为单位的图像坐标系坐标。

2）像平面坐标系。坐标系是以像素为单位的坐标系，而像平面坐标系x′y′是连续坐标系，或物理单位坐标系。用（u，v）表示图像坐标，（x′，y′）表示像平面坐标。x′y′坐标系的原点定义在摄像机光轴与图像平面的交点（u₀，v₀），此交点称为主点。在x′轴和y′轴方向上像素之间的距离为S_x和S_y。则两坐标系之间的关系为

表示成矩阵形式，即

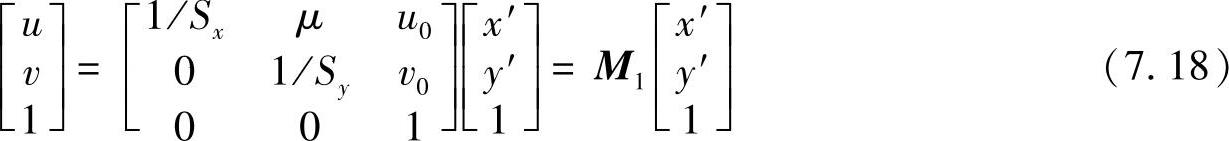
式中，矩阵M称为内参数矩阵。由于摄像机制造及工艺等原因，像素点可能发生畸变，μ定义为考虑像素点畸变的畸变因子，有时也称图像不确定因子，倾斜因子等。其形成原因是在实际图像采集系统中，由于CCD安装平面与镜头光轴不垂直，存在倾角误差等因素。图像坐标系与像平面坐标系如图7.7所示。

综上所述，当世界坐标、摄像机坐标、像平面坐标、图像坐标都分开且不考虑畸变影响时，通用摄像机模型可表示为

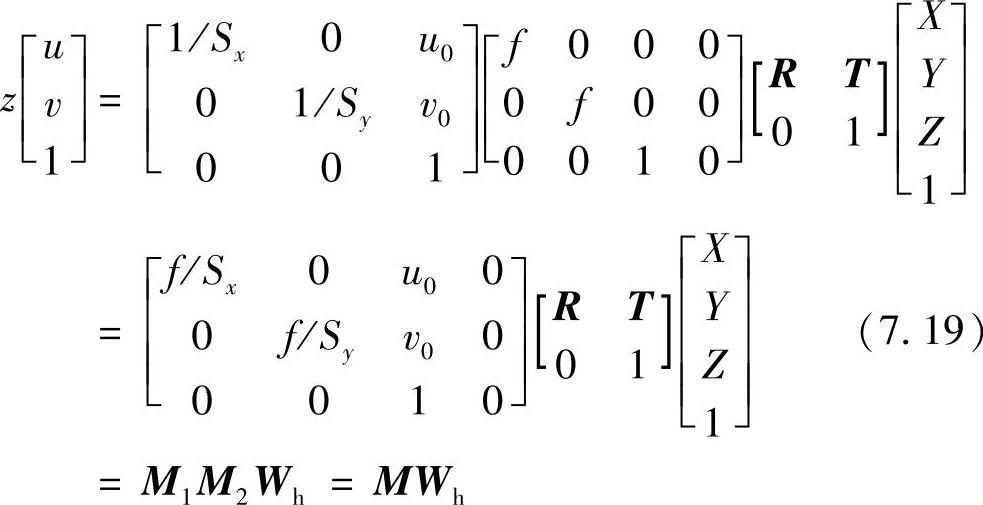
M₁只与摄像机内部结构有关，称摄像机内部参数。主要包括：x方向尺度因子f_u=f/S_x，y方向尺度因子f_v=f/S_y，像主点在图像坐标系中的坐标（u₀，v₀），畸变因子μ。M₂只与摄像机相对于世界坐标系的方位有关，称为摄像机的外部参数，外部参数可以定义为是12个，包括：旋转矩阵R的9个参数和平移矩阵T的3个参数。也可以定义为6个，包括：旋转矩阵R的3个偏转角和平移矩阵T的3个参数。W_h为空间点在世界坐标系下的齐次坐标。

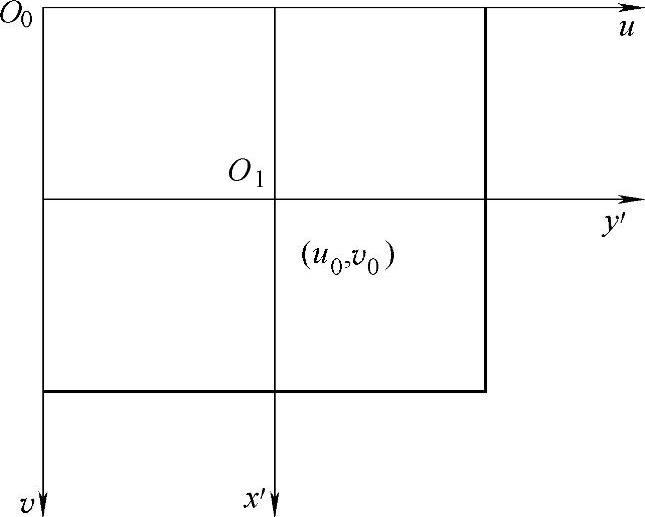
图7.7 图像坐标系与像平面坐标系

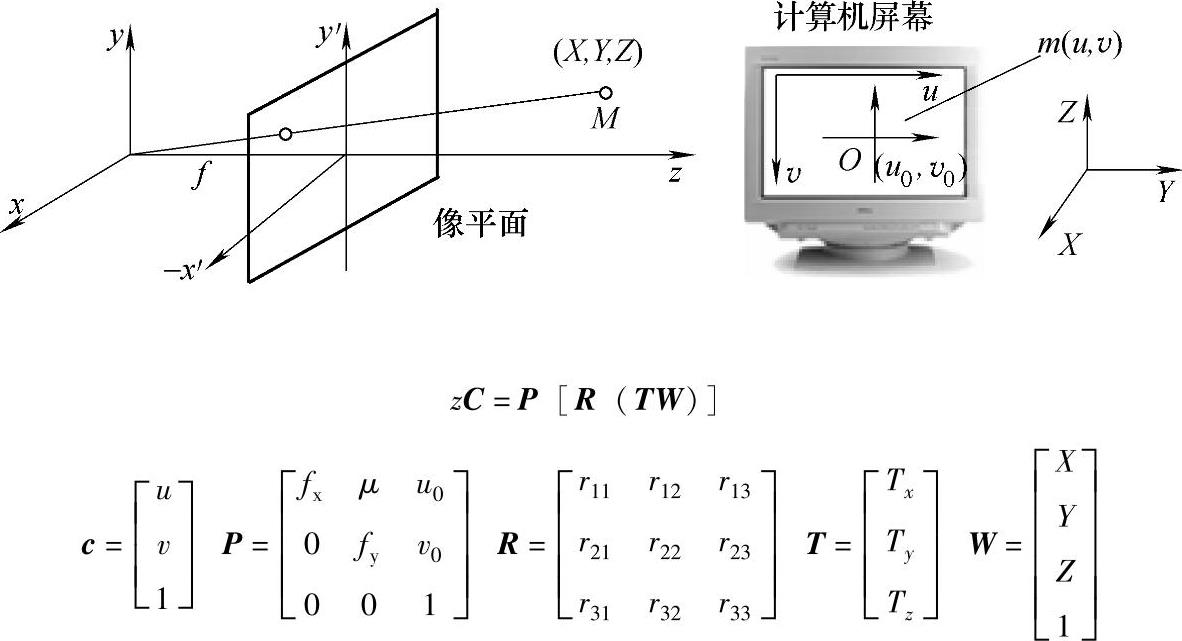
图7.8 摄像机模型示意图

上述摄像机模型为线性模型，如果已知摄像机的内外参数，即已知M矩阵，对任何空间点，知道其世界坐标，就可以求出其图像像素坐标系中该图像点的坐标。反过来，如果已知空间某点的图像坐标，即使已知其内外参数，空间坐标也不是惟一确定的，它对应空间的一条射线。

当考虑摄像机镜头畸变时，摄像机模型为非线性模型，即