将瞳孔目标模型定义为X={C_x，C_y，H_x，H_y，V_x，V_y，a，b，θ，ad}。其中，C_x和C_y为瞳孔目标中心在图像中x和y方向的坐标值；H_x和H_y为观测窗口的半窗宽和半窗高；V_x和V_y为瞳孔目标分别在图像中的x和y方向的运动速度；a和b为瞳孔椭圆的长半轴和短半轴的长度；θ为瞳孔椭圆长轴与竖直方向之间的夹角；ad为尺度扰动幅度。

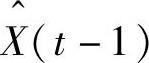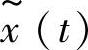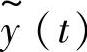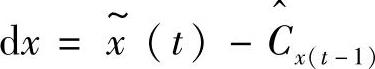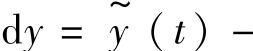
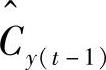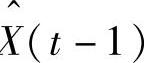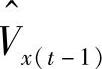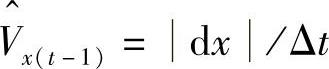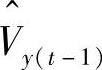初始时刻目标的状态值已经由初始化处理得出。设t-1时刻瞳孔目标状态的卡尔曼估计为；设t时刻粒子滤波状态估计值中的矩形框中心x方向坐标为；y方向坐标为；当t时刻粒子滤波估算工作完成后，令；；将X中的更新为；更新为。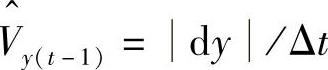

1.状态转移模型和观测

根据状态转移模型进行预测，将上述不同值的dx及dy分为四种情况，状态转移矩阵根据这几种情况的不同而不同。

令状态转移模型为X（t）=Φ·X（t-1）+ω（t-1）；瞳孔状态（观测值）矢量为O（t），噪声矢量为v（t）。其中，ω（t-1）、v（t）为均值为0的高斯白噪声，令v（t）的噪声方差为

1。状态转移矩阵Φ如下：

dx≠0，dy=0时有

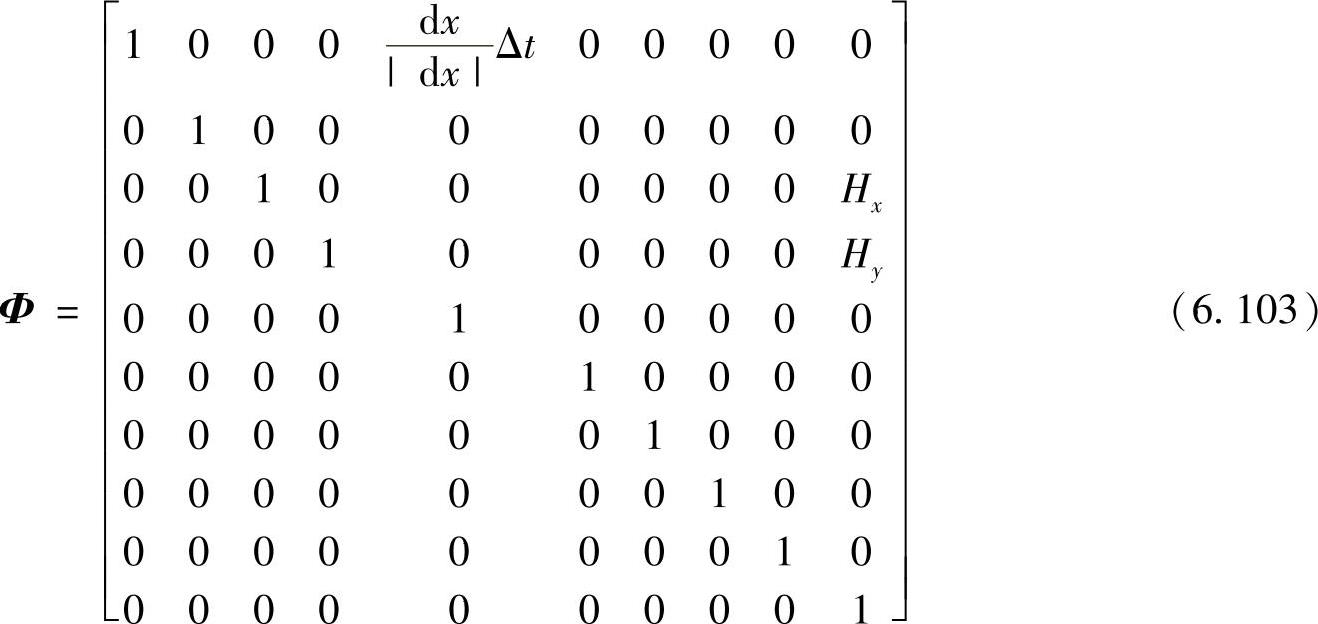
dy≠0，dx=0时有

dx≠0，dy≠0时有

dx=0，dy=0时有

(www.daowen.com)

状态转移模型中的噪声矢量V由两部分组成：η（t）～N（0，σ²），ν（t）～U（0，1）。

这里利用对差分图像中粒子滤波跟踪区域瞳孔状态检测来完成观测工作。检测流程如图6.26所示。

设t时刻经检测得出的瞳孔状态矢量为O（t）。

2.目标状态的最终估计

求出α后，可用于对卡尔曼滤波预测值进行调整。在卡尔曼滤波算法中新的估计值计算如下：

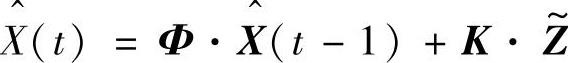
式中，K是卡尔曼增益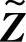，是观测差，即修正值。

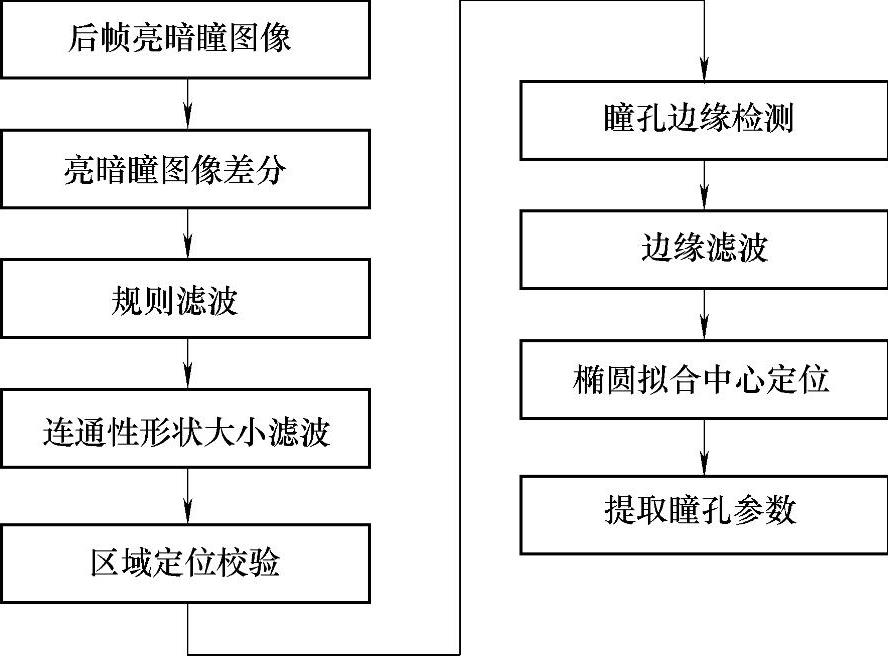
图6.26 瞳孔状态矢量检测（观测）流程

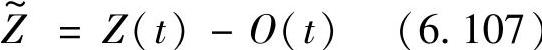
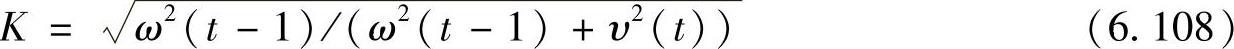
这样就完成了单步卡尔曼滤波算法的目标状态估计步骤。其得出的目标状态估计为跟踪算法的最终估计。

当卡尔曼滤波跟踪步骤结束后，将所估计的t时刻的瞳孔的位置中心等参数作为粒子滤波t时刻状态矢量中的x和y的估计值，送入下一步预测环节当中。如此循环，便实现了基于粒子滤波-单步卡尔曼滤波算法的瞳孔跟踪过程。