粒子滤波（Particle Filter）是求解贝叶斯概率的一种实用算法，其含义是指目标状态传播的后验概率可以用若干个粒子来近似表示。

6.2.1.1 动态系统的状态空间模型

假设实际系统的状态序列为{x_k，k∈N}，其中k为时间序列标号，x_k∈Rⁿ表示时间标号为k的状态矢量。状态关系为

x_k=f（x_k-1，w_k-1） （6.32）式中，f（）为系统的非线性状态转移函数。{w_k-1，k∈N}是一个独立同分布的噪声序列。另外，也可以用转移概率矩阵形式来描述，即

p（x_kx_k-1）k≥0 （6.33）系统观测到的序列为{z_k，k∈N}，其中z_k∈Rⁿ表示时间标号为k的观测矢量。它与系统状态之间的关系为

z_k=h（x_k，v_k） （6.34）

式中，h为系统的非线性观测函数。{v_k，k∈N}是一个独立同分布的噪声序列。另外，也可以用转移概率矩阵形式来描述，即

p（z_kx_k）k≥0 （6.35）

状态空间模型最重要的问题是在观测矢量z₁∶k=（z₁，…，z_k）和初始分布p（x₀）的基础上，估计出状态矢量x_k+1。时间序列中的参数估计和估计的似然计算、平稳或非平稳时间序列的构建都能通过状态估计来实现。对应i取值的三种不同情况i=0，i>0，i<0，状态估计问题被划分为三种不同的类型，即滤波、预测和平滑：

对于滤波问题，需要计算滤波密度p（x_kz_1∶k），滤波密度实际上是后验概率密度，从滤波密度可以计算系统状态的各种估计，如均值为

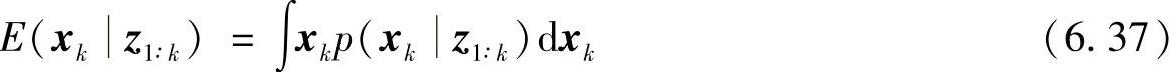
6.2.1.2 贝叶斯滤波原理

贝叶斯滤波原理的实质是用所有已知信息来构造系统状态变量的后验概率密度。即用系统状态转移模型预测状态的先验概率密度，再使用最近的观测值进行修正，得到后验概率密度。这样，通过观测数据z₁∶k来递推计算状态x_k取不同值时的置信度p（x_kz₁∶k），以此获得状态的最优估计[4，5]。其基本步骤分为预测（Prediction）和更新（Updating）两步。

假设已知概率密度的初始值p（x₀z₀）=p（x₀），并定义x_k为系统状态，如目标的运动状态：位移、速度、加速度、旋转、尺度等。z_k为对系统的观测值。递推过程分为两个步骤：

（1）预测（Predection）

即由系统的状态转移模型，在未获得k时刻观测值时，实现先验概率p（x_k-1z₁∶k_-1）至先验概率p（x_kz₁∶k_-1）的推导。假设在k-1时刻，p（x_k-1z₁∶k_-1）是已知的，对于一阶马尔可夫过程，k-1时刻的概率仅与k-2时刻的概率有关，由Chapman-Kolmogorov方程

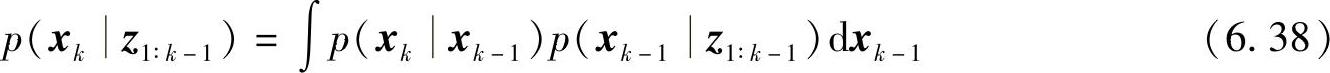
即得到不包含k时刻观测值的先验概率，并可以由系统的状态转移概率p（x_kx_k-1）来计算。

（2）更新（Update）

根据系统的观测模型，在获得k时刻的观测值z_k后，实现先验概率p（x_kz_1∶k-1）至后验概率p（x_kz_1∶k）的推导。

获得观测值z_k后，由贝叶斯公式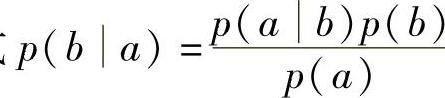可得

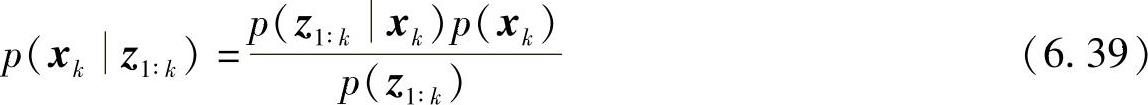
将观测量z_k独立出来，有

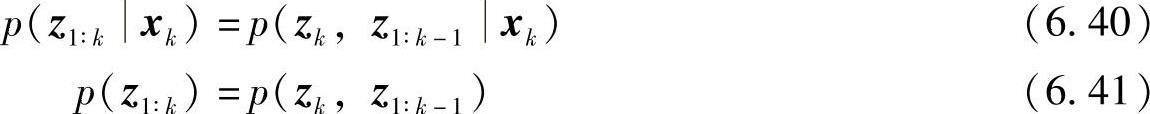
将上两式代入式（6.39），得

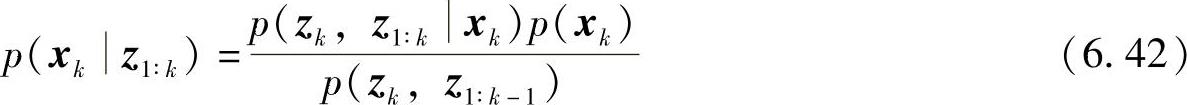
由条件概率定义p（a，b）=p（ab）p（b），有

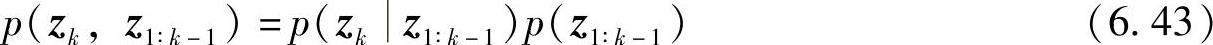
由联合分布概率公式p（a，bc）=p（ab，c）p（bc），有

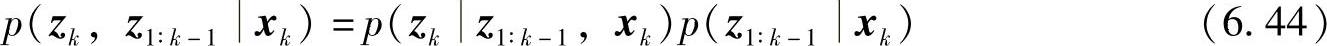
又根据贝叶斯公式，得到

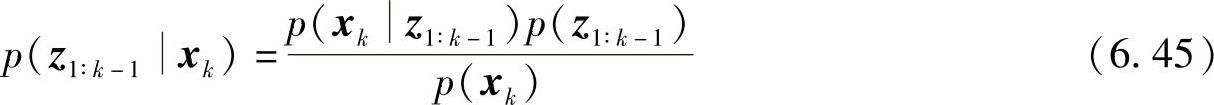
将式（6.43）、式（6.44）和式（6.45）代入式（6.42）得

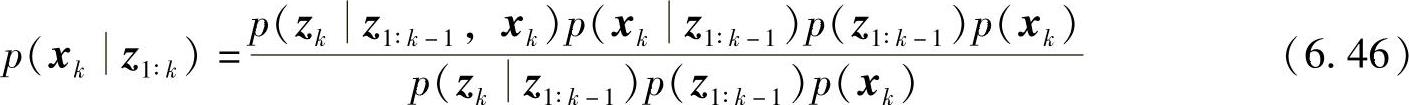
假设各个观测是相互独立的，则有

将式（6.47）代入式（6.46），并消去分子和分母的共同项p（z₁∶k_-1）p（x_k）得

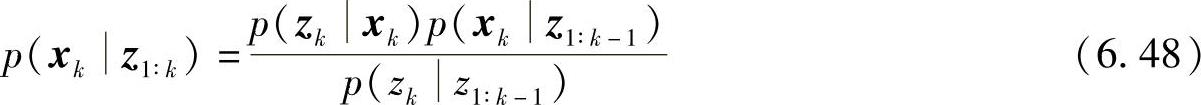
式中，p（z_kx_k）称为似然性（Likelihood），表征系统状态由x_k-1转移到x_k后和观测值的相似程度；p（x_kz_1∶k-1）为上一步系统状态转移过程所得，称为先验概率（Prior）；p（z_kz_1∶k-1）称为证据（Evidence），一般是一个归一化常数。

这样式（6.38）和式（6.48）构成了一个由先验概率p（x_k-1z_1∶k-1）推导至后验概率p（x_kz_1∶k）的递推过程。即首先由k时刻的先验概率p（x_k-1z_1∶k-1）（也就是k-1时刻的后验概率）出发，利用系统状态转移模型来预测系统状态的先验概率密度p（x_kz₁∶k_-1），再使用当前的观测值z_k进行修正，得到k时刻的后验概率密度p（x_kz_1∶k）。

由上两步求得状态变量x_0∶k的后验概率分布p（x_0∶kz_1∶k）后，根据蒙特卡罗仿真原理，任意函数g（）的数学期望为

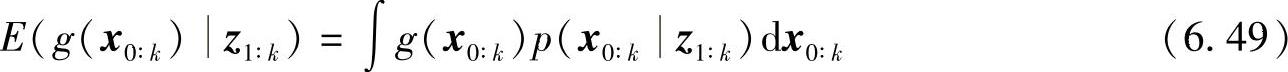
假设从条件后验概率密度p（x_0∶kz_1∶k）独立随机抽样得到粒子{x⁽ⁱ⁾_0∶k}^N_i=1，有

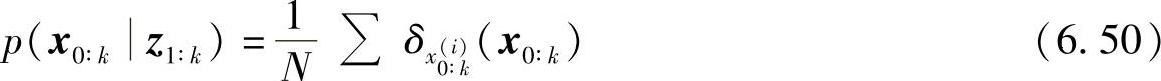
式中，δ_x（）为点x处的狄拉克函数，则g（x₀∶k）的期望可以用下式近似

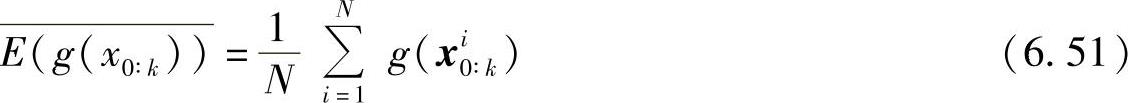
式中，离散样本{xⁱ_0∶k，i=0，…，N}是从后验概率分布函数中产生的N个点的独立同分布序列。根据大数定理，由于{xⁱ_0∶k，i=0，…，N}间相互独立，当N→∞时，E（g（x_0∶k））绝对收敛于E（g（x_0∶k））。

由式（6.38）和式（6.48）可以得到一种求后验概率的递推方法，但这只是理论上的处理方法。实际上由于式（6.38）的积分很难实现，不可能进行精确分析。但在某些限制条件下，有多种实现方法，如卡尔曼滤波等。

6.2.1.3 蒙特卡罗方法

1.蒙特卡罗方法概述

蒙特卡罗方法的基本思想：为了求解数学、物理、工程技术及生产管理方面的问题，首先建立一个概率模型或随机过程，使它的参数等于问题的解；然后，通过对模型和过程的观察或抽样试验来计算所求参数的统计特征；最后，给出所求解的近似值，而解的精度可用估计值的标准误差来表示。

因此，蒙特卡罗方法解题是以一个概率模型为基础的。按照这个模型所描绘的过程，通过部分模拟试验的结果，作为问题的近似解。蒙特卡罗方法解题过程可以归结为以下三个步骤：

（1）构造或描述概率过程

对于本身具有随机性质的问题，主要是正确描述和模拟这个概率过程。对于本来不是随机性质的确定性问题，如定积分计算、线性方程组求解和偏微分方程边值问题等，用蒙特卡罗方法求解，就必须事先构造一个人为的概率过程，使它的某些参量正好是所求解问题的解。即将不具有随机性质的问题，转化为随机性质的问题。

（2）实现从已知概率分布抽样

由于各种概率模型都可看作是由各种概率分布构成的，因此产生已知概率的随机变量，是实现蒙特卡罗模拟试验的基本手段。所以，蒙特卡罗方法也叫随机抽样技术。最简单、最基本、最重要的概率分布是（0，1）上的均匀分布。随机数就是具有这种均匀分布的随机变量。随机数序列是具有均匀分布的总体的简单子样，即具有这种分布的相互独立的随机变数序列。产生随机数的问题，就是根据这个分布的抽样问题。在计算机上可以产生随机数，但不能重复且使用不便。另一种方法是用数学递推公式产生，这样产生的随机数序列，与真正的随机数序列不同，所以称为伪随机数或伪随机数序列。多种统计检验表明，它与真正的随机数或随机数序列具有相似的性质，因此可作为真正的随机数来使用。由已知分布随机抽样的各种方法都是借助随机序列来实现的，因此随机数是实现蒙特卡罗模拟的基本工具。

（3）建立各种估计量

一般来说，构造了概率模型并从中抽样，就确定了一个随机变量作为所求问题的解的估计量。建立各种估计量，相当于对模拟试验的结果进行考察和登记并从中得到问题的解。

2.蒙特卡罗积分

设D为n维空间Rⁿ上的一个区域，考虑多重积分：

I=∫_DG（x）dx （6.52）式中，D为积分区域。由一维积分变成多维积分时其处理难度和多样性将大大增加，实现上存在很大难度。因此当维数超过4时，一般都采用蒙特卡罗方法求解^[6，7]。

蒙特卡罗积分就是将积分值看成是某种随机变量的数学期望，并用抽样方法加以估计，可以写成

I=∫_Dg（x）p（x）dx （6.53）

式中，p（x）满足：p（x）≥0，。因此需要对被积函数G（x）进行适当分解，使得G（x）=g（x）p（x），通常将p（x）看成是状态变量的概率密度函数，只要积分有界，则I可看成是g（x）的数学期望，即I=E[g（x）]。对于贝叶斯估计问题，所关心的是状态在给定测量条件下的后验概率密度函数，即p（x）=p（xy_1∶n）。令g（x）=x，即可得到状态的最小方差估计。

现从p（x）抽取随机变量x的N个样本{x_i}^N，则g（x_i）的算术平均值为

可以证明g_N是I的无偏估计。蒙特卡罗积分与基于网络的直接积分方法相比，前者积分过程中所使用的样本点是按密度函数p（x）自动抽取的，而后者需要人为地对积分空间进行划分。根据大数定理，当{x_i}^N中的样本相互独立，且N→∞时，样本的算术均值g_N以概率1收敛到I，即

若有不为零的有界方差σ²存在，即

σ²=∫_D（g（x）-I）²p（x）dx<+∞ （6.56）

则在1-α置信水平下，有

即蒙特卡罗积分方法的误差阶为σ（N^-1/2），它与积分维数无关，故很适用于高维积分问题。由式（6.57）可见，给定置信水平1-α，误差由σ和N决定。要减少误差，要么增大样本数目N，要么降低方差σ²，通常降低方差的各种技巧有重要性抽样、系统抽样、分层抽样等。(www.daowen.com)

3.重要性采样

蒙特卡罗积分方法的前提是可以得到N个服从p（x）分布的随机样本。通常情况下，该密度分布函数并不能写成一般的解析形式，很难直接得到样本，必须用随机抽样算法。重要性抽样就是其中典型的抽样算法。

考虑式（6.53）的计算，取积分区域D上任一联合概率密度q（x），并满足条件：当g（x）p（x）≠0时，q（x）≠0。若令

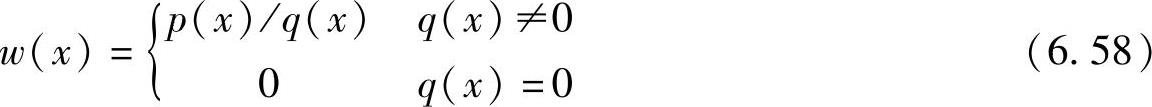
则有

I=∫_Dg（x）p（x）dx=∫_Dg（x）w（x）q（x）dx （6.59）令{x_i}^N_i=1为服从q（x）分布的随机抽样，蒙特卡罗估计可由样本均值给出：

习惯上称q（x）为重要性函数，w（x）为重要性系数。要找到一个重要性函数q（x），使得g（x）w（x）的方差比g（x）的方差更小。

6.2.1.4 粒子滤波器

粒子滤波方法的基本思想是利用一组带有相关权值的随机样本，以及基于这些样本的估算来表示后验概率密度。当样本数非常大时，这种估计将等同于后验概率密度。具体地说，就是在状态空间中寻找一组随机样本对条件后验概率密度p（x_0∶kz_1∶k）进行近似，以样本均值代替E（g（x_0∶k）z_1∶k），从而获得状态的最小方差估计。其实现的关键，在于寻找服从p（x_0∶kz_1∶k）分布的随机样本。这些样本常被称为粒子。

1.贝叶斯重要性采样（BIS）

根据式（6.51），一个函数的后验分布可以用一系列离散的粒子来近似表示，近似程度依赖于粒子的数量N。通常函数的后验分布密度是无法直接得到的，而贝叶斯重要性采样定理描述了这个问题的求解方法。

贝叶斯重要性采样（Bayesian Importance Sampling，BIS）定理是先从一个已知的容易采样的重要性函数q（x_0∶kz_1∶k）中采样，通过对重要性函数的采样粒子点进行加权来近似获得p（x_0∶kz_1∶k）。

对式（6.49）变形可得

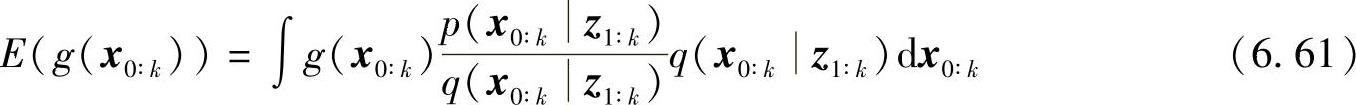
根据贝叶斯公式

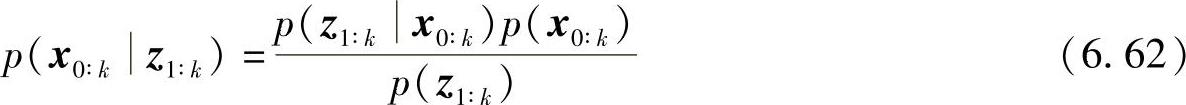
有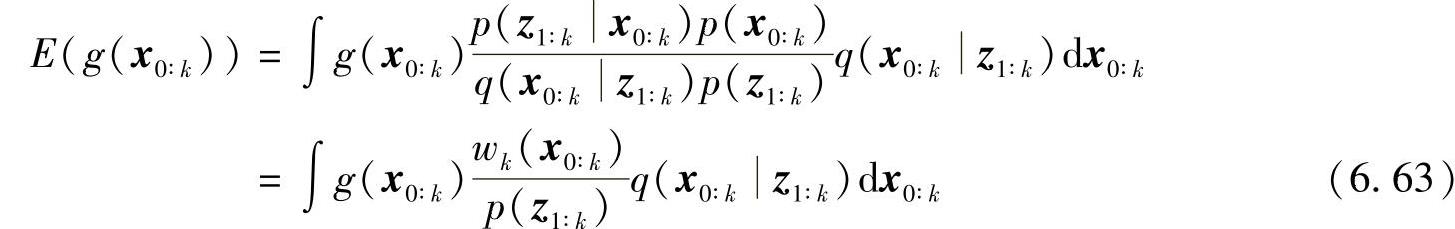

其中权值

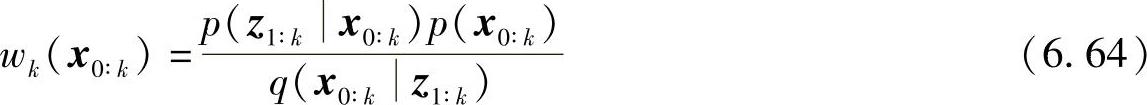
其中

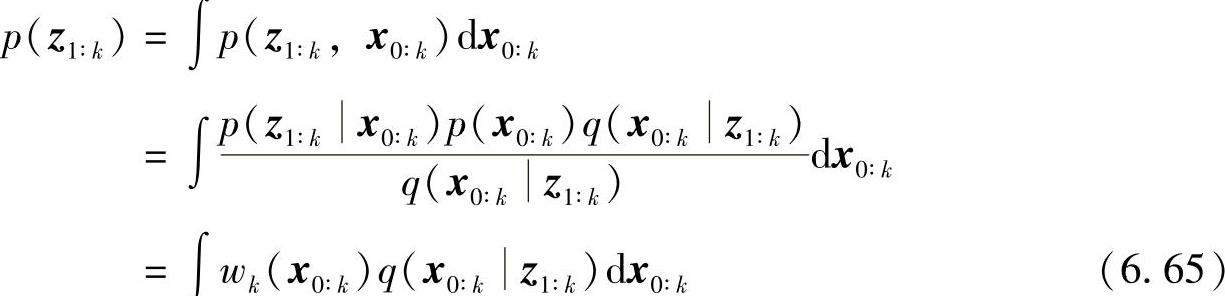
将式（6.65）代入（6.63）得

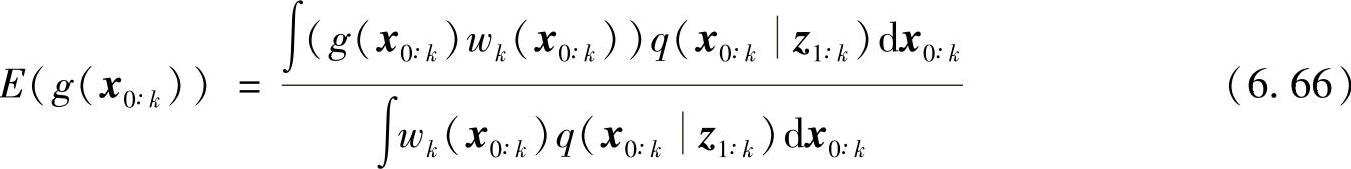
从重要性函数中采样后，数学期望近似表示为

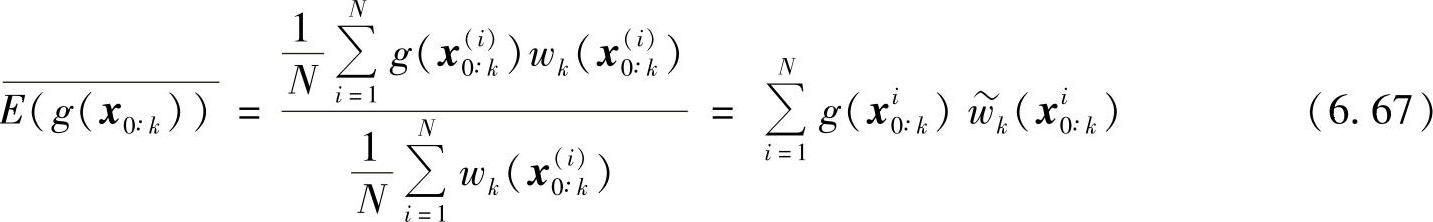
式中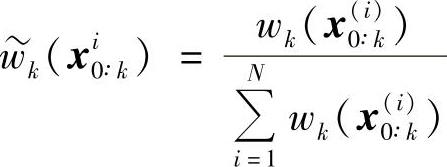，为归一化权值；x⁽ⁱ⁾_0∶ik为从q（x_0∶kz_1∶k）中抽取的粒子。

2.序贯重要性采样

重要性采样用易抽样的q（x_0∶kz_1∶k）代替难于抽样的p（x_0∶kz_1∶k），是一种易于实现的蒙特卡罗方法。但每次新的观测数据z_k出现后，都要重新计算包括先前时刻在内的整个状态序列的重要性权值，各个时刻的估计值也要更新，算法不具有递推形式。因此，又提出了一种改进策略——序贯重要性采样。

为了对后验分布进行递推形式估计，将上述BIS算法写成序列形式。此时，重要性函数q（x_0∶kz_1∶k）可以分解为

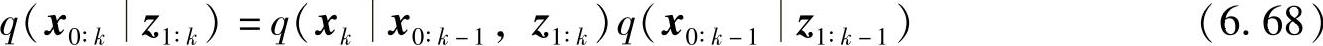
假设系统的状态和观测模型服从马尔可夫过程，在给定状态下测量是相互独立的，即

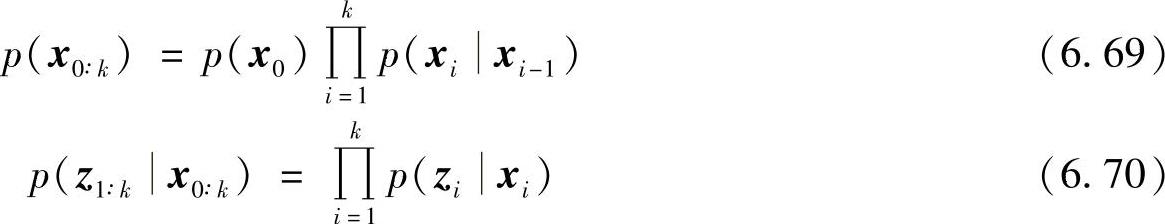
通过由q（x_0∶k-1z_1∶k-1）得到的支撑点xⁱ_0∶k-1和由q（x_kx_0∶k-1，z_1∶k-1）得到的支撑点xⁱ_k，可以获得新的支撑点xⁱ_0∶k。则权值的更新公式可以做进一步推导，将式（6.68）代入式（6.64）得

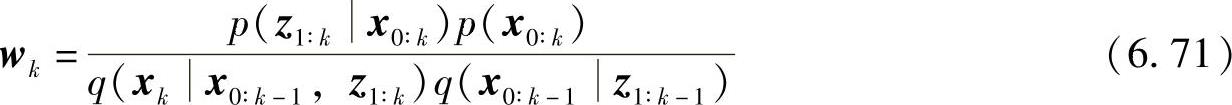
又由式（6.64）可得

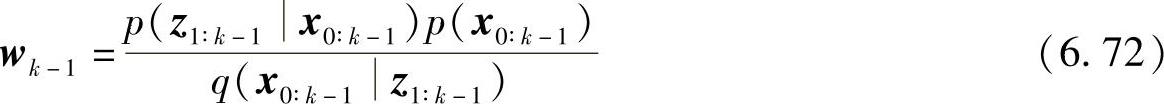
由式（6.69）和式（6.70），合并式（6.69）和式（6.72）可得

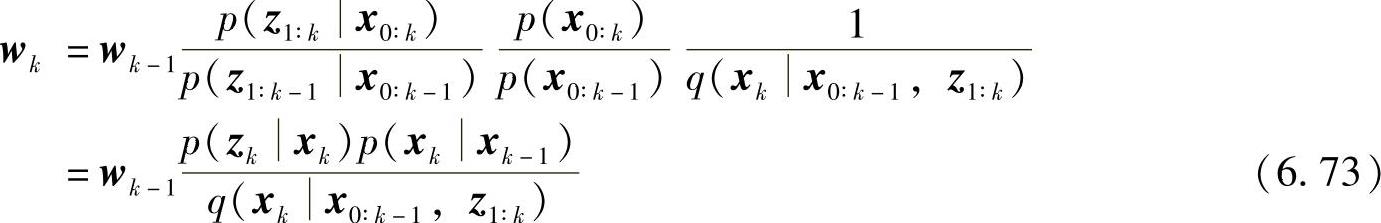
更进一步，如果状态估计的过程是最优估计，则重要性概率密度函数只依赖于x_k-1和z_k，即

q（x_kx_0∶k-1，z_1∶k）=q（x_kx_k-1，z_1∶k） （6.74）进行抽样之后，对每个粒子赋予权值w_kⁱ，将式（6.74）代入式（6.73）得

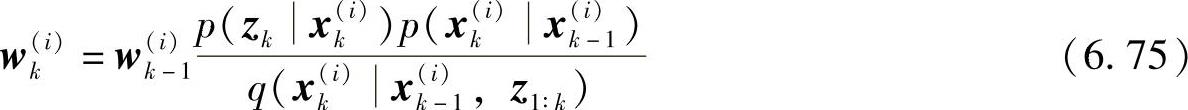
式（6.75）是重要性权值函数的递推形式，称为序贯重要性抽样。假设，已知k-1时刻以前的采样粒子{x⁽ⁱ⁾_0∶k-1}^N_i=1，以及k-1时刻的归一化权值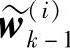。记为{x^（i)_0∶k-1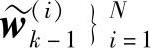，。当k时刻的新观测数据z_k到来时，递推算法可以归纳为

1）从重要性函数q（x_kx⁽ⁱ⁾_0∶k-1，z_1∶k）抽样得到粒子{xk^（i）}^N_i=1；

2）根据式（6.75）计算k时刻权值：

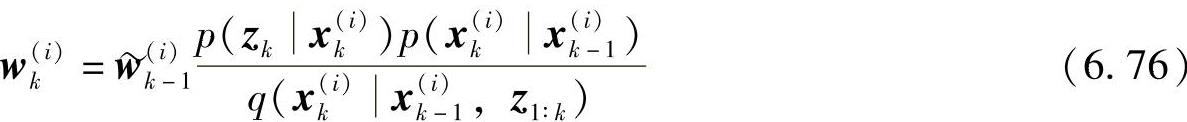
3）归一化权值：

把粒子和k时刻权值记为{x^（i）_0∶ik，。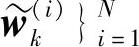

3.粒子退化现象及消除退化的关键技术

BIS算法存在的一个基本问题，就是退化现象。即经过几步迭代递推后，权重的方差随着时间增大，许多粒子的权重变得非常小，只有少数几个粒子具有较大的权值，大量的计算浪费在小权值粒子上。解决退化问题一般采用两种方法：选取适当的重要性函数和进行重采样。

（1）选取适当的重要性函数

主要原则：

1）使权系数方差最小；

2）从重要性密度函数中抽样容易实现。重要性函数q（x_kⁱx_kⁱ-1，z₁∶k）的最优选取方法是

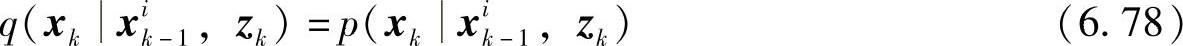
这种情况下，重要性函数q（x_kx_kⁱ-1，z_k）等于真实分布，则对于任意粒子x_kⁱ-1，都有权重wⁱ_k=1/N，var（w_kⁱ）=0，此时有

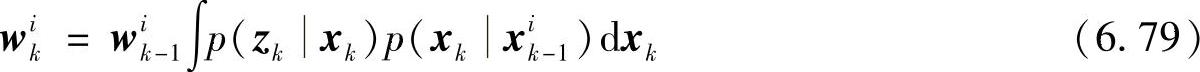
上述参考分布的最优选择方法有两个严重缺陷，首先是真实分布p（x_kxⁱ_k-1，z_k）通常无法得到，其次是积分式一般无法求解。因此，最常见的参考分布选择为先验密度，即

代入式（6.75）得

这种方法直接且容易实现，但没有考虑使用新的观测值。由于实现的简易性，这样的重要性函数选择是最常用的。

（2）重采样

重采样方法的基本思想是通过对后验概率密度再采样N_s次，产生新的支撑点集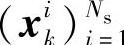，保留或复制具有较大权重的粒子，剔出权重较小的粒子，使得原来的带权样本{xⁱ_0∶k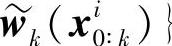，映射为等权重样本{xⁱ_0∶k，1/N}，这样式（6.67）变化为

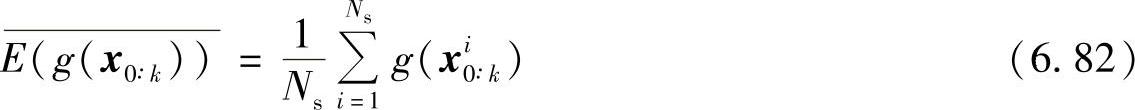
图6.7所示为粒子重采样原理示意。t-1时刻的先验概率由若干权值为1/N的粒子近似表示，重采样由以下步骤完成：

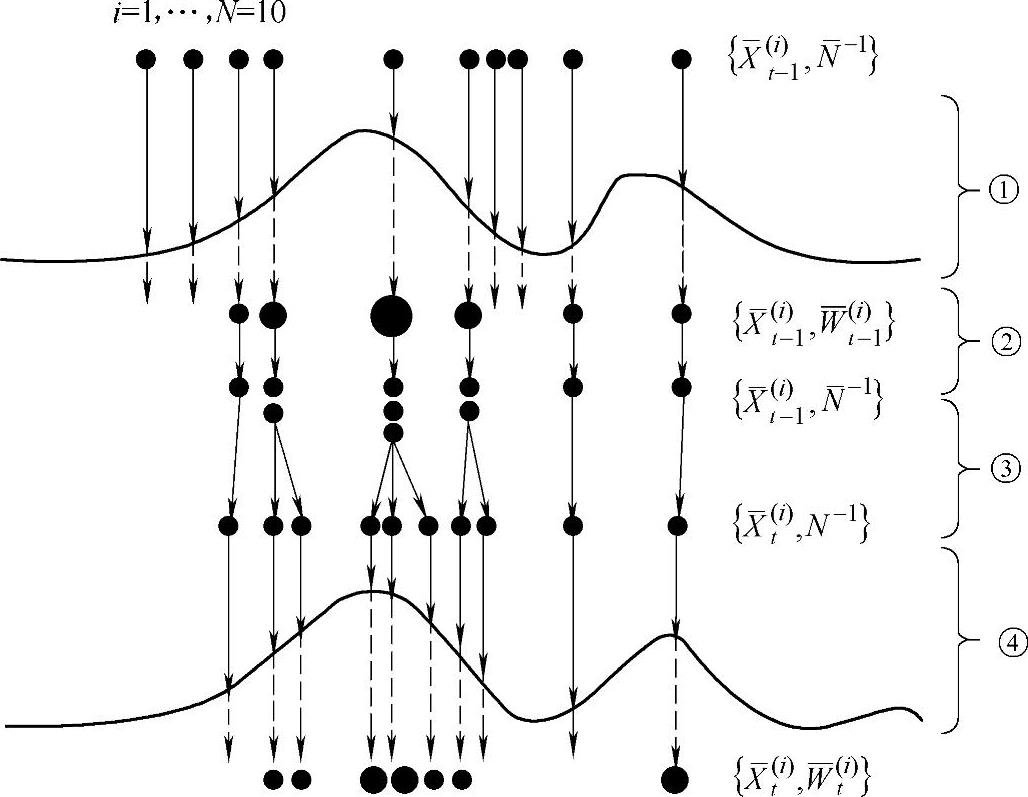
图6.7 重采样示意图

1）经过系统观测后，重新计算粒子的权值w^（i）_t-1，比较符合实际情况的粒子（波峰处的粒子）被赋予较大的权值（图6.7中面积较大的粒子），而偏离实际情况的粒子（即波谷处的粒子）被赋予较小的权值（图6.7中面积较小的粒子）。

2）重采样过程中，权值大的粒子衍生出较多的“后代”粒子，而权值小的粒子相应的“后代”粒子也较少，而且“后代”粒子的权值被重新设置为1/N。

3）系统状态转移过程，通过加入随机量预测每个粒子在t时刻的状态。

4）t时刻的观测过程，与1）一致，并且通过若干粒子的加权得到目标状态的最终表示。