卡尔曼滤波建立在线性代数和隐马尔可夫（Hidden Markov）模型上。其基本动态系统可以用一个马尔可夫链表示，该马尔可夫链建立在一个被高斯噪声（即正态分布的噪声）干扰的线性算子上的。系统状态可以用一个实矢量表示。随着离散时间的每一次增加，线性算子就会作用在当前状态上，产生一个新的状态，并会带入一些噪声，同时系统的控制信息也会被加入。同时，另一个受噪声干扰的线性算子产生这些隐含状态的可见输出。卡尔曼滤波器的模型如图6.1所示，图中圆圈代表矢量（如u），正方形代表矩阵（如h），星形代表高斯噪声（如v），高斯噪声对应的协方差矩阵在星形的右下角标出（如R），k-1、k、k+1分别代表上一时刻、当前时刻和下一时刻。其中，R代表了观测信息的质量，F为状态转移阵，将过去k-1时刻状态和现在的k时刻状态联系起来；B代表控制输入u（k）的增益矩阵；H为观测矩阵，表示状态变量X（k）对测量变量H（k）的增益。

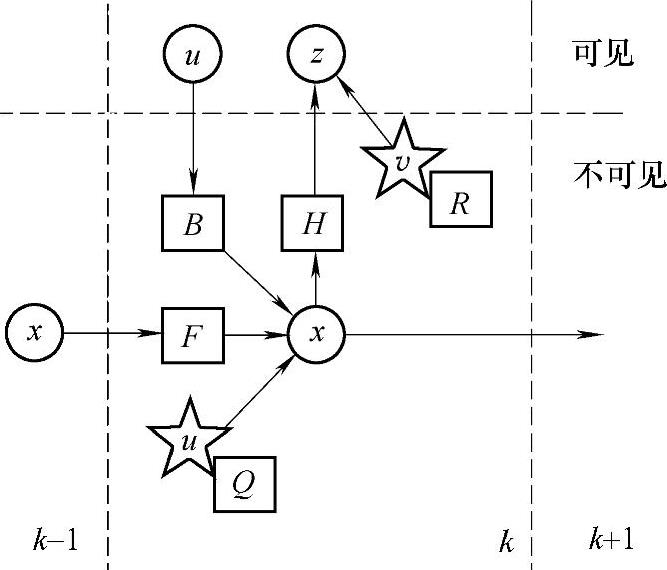
图6.1 卡尔曼滤波模型

卡尔曼滤波是随机信号估计的算法之一，采用状态空间法在时域内设计滤波器，避免了在频域内对信号功率谱进行分解的麻烦。同时卡尔曼滤波算法采用递推计算方式，将实时观测信息和历史信息融合于估计值中，从而不必存储时间过程中的观测量。在状态空间方法中，引入了状态变量和状态空间概念。状态是比信号更广泛、更灵活的概念，它非常适合处理多变量系统和信号估计问题，信号可视为状态或状态的分量。系统状态变量是能体现系统特征、特点和状况的变量。状态空间方法的关键技术包括状态空间模型和状态估计方法。状态方程是描写状态变化规律的模型，它表示了相邻时刻的状态转移变化规律。观测方程描写状态观测的信息，通常含有观测噪声且只能对部分状态变量进行观测。卡尔曼滤波是根据观测信息求系统状态的最优估计。

6.1.1.1 离散卡尔曼滤波

1.离散卡尔曼滤波基本方程

设k时刻被估计状态X（k）受系统噪声序列W（k-1）驱动，驱动机理由下述状态方程描述：

X（k）=ϕ（k，k-1）X（k-1）+Γ（k-1）W（k-1） （6.1）

对X（k）的量测满足线性关系，量测方程为

Z（k）=H（k）X（k）+V（k） （6.2）

式中，ϕ（k，k-1）为k-1时刻至k时刻的一步转移矩阵；Γ（k-1）为系统噪声驱动矩阵；H（k）为量测矩阵；V（k）为量测噪声序列；W（k）为系统激励噪声序列。同时，W（k）和V（k）满足

E[W（k）]=0，Cov[W（k），W（j）]=E[W（k）_kW（j）^T]=Q（k）σ_kj （6.3）

E[V（k）]=0，Cov[V（k），V（j）]=E[V（k）V（j）^T]=R（k）σ_kj （6.4）

Cov[V（k），V（j）^T]=0 （6.5）

式中，Q（k）为系统噪声序列的方差距阵，假设为非负定阵；R（k）为量测噪声序列的方差距阵，假设为正定阵。若已知k时刻的量测值为Z（k），则X（k）的估计X（k）按下述步骤求解。

（1）估计误差方程

设k时刻状态矢量为X（k），估计值为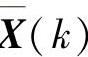，误差矢量为e（k）=X（k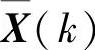）-，则估计误差方差矩阵为

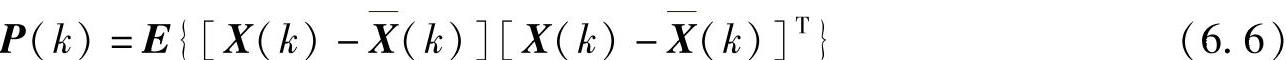
估计误差方差为

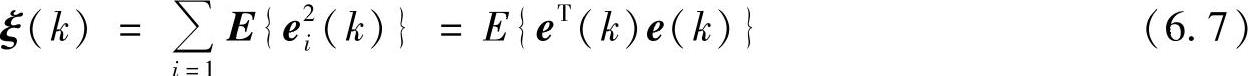
卡尔曼滤波根据测量矢量Z（k），求出状态矢量X（k）的最佳估计值X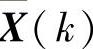，使得估计误差的方差ξ（k）为最小。

（2）预测误差方差矩阵

根据估计方差最小理论，k+1时刻的状态矢量估计值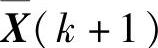，等于状态矢量X（k+1）在给定{Z（1），Z（2），…，Z（k）}时的条件均值，即

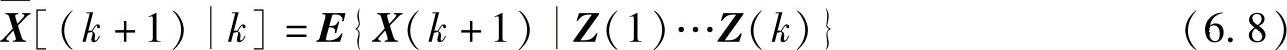(www.daowen.com)

将此式带入状态方程，其中E{X（k+1）Z（1）…Z（k）}=0，得到状态矢量X（k）在k+1时刻的最优预测矢量，即

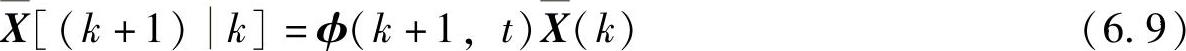
同理，可以得到观测矢量的最优预测矢量为

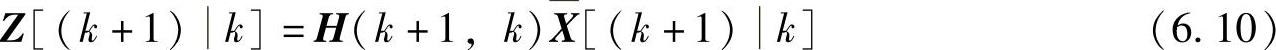
联立求解，得到估值误差方差矩阵为

P（k+1k）=ϕ（k+1，k）P（k）ϕ^T（k+1，k）+Q（k） （6.11）

（3）滤波估值方程

在对k时刻状态矢量X（k）进行预测后，根据实际得到的k+1时刻的观测值Z（k+1）对预测值X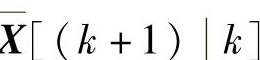进行修正，即可得到k+1时刻的状态矢量X（k+1）的滤波估值X（k+1），有

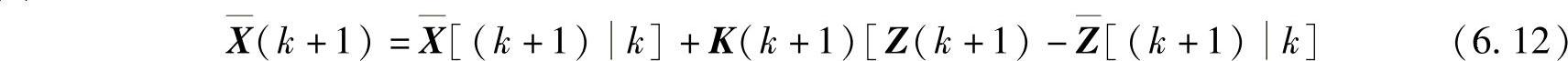
式中，K（k+1）称为增益矩阵，有

K（k+1）=P（k+1k）H^T（k+1）[H（k+1）P（k+1k）H^T（k+1）+R（k）]^-1 （6.13）得到滤波误差方差矩阵为

P（k+1）=（I-K（k+1）H（k+1））P（k+1k） （6.14）

在一个滤波周期内，从卡尔曼滤波使用系统信息和量测信息的先后次序来看，卡尔曼滤波具有两个明显的信息更新过程——时间更新过程和量测更新过程。式（6.9）说明了根据k-1时刻的状态估计预测k时刻状态估计方法，式（6.11）对这种预测的质量作了定量描述。这两个公式的计算仅使用了与系统动态特性有关的信息，如一步转移阵、噪声驱动阵、驱动噪声的方差阵等。从时间的推移过程来看，这两个公式将时间从k-1时刻推进到k时刻。所以，这两个公式描述了卡尔曼滤波的时间更新过程。其余各式用来计算对时间更新值的修正量，这些修正量由时间更新的质量优劣P（k，k+1）、量测信息的质量优劣R（k）、量测与状态的关系H（k）及具体的量测值Z（k）所确定。所有这些方程围绕着如何合理利用Z（k），描述了卡尔曼滤波的量测更新过程。卡尔曼滤波的时间更新过程和量测更新过程如图6.2和图6.3所示。卡尔曼滤波具有两个计算流程——滤波计算流程和增益计算流程。

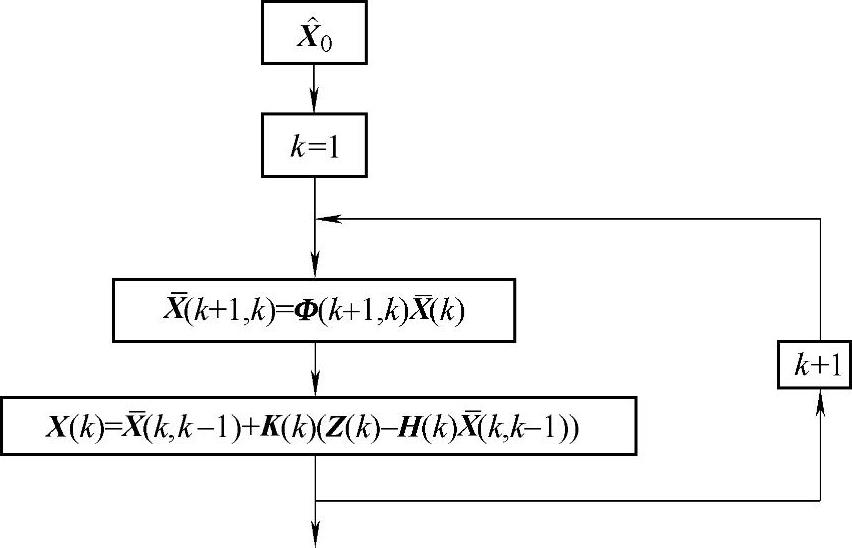
图6.2 卡尔曼滤波计算流程

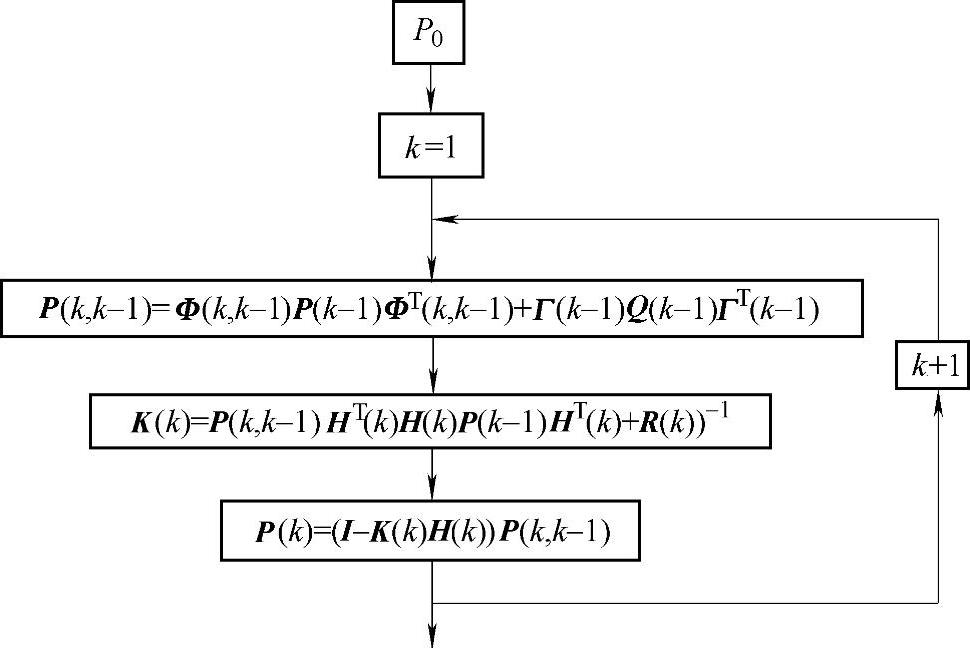
图6.3卡尔曼滤波增益流程

其中，增益计算流程是独立计算流程，而滤波计算流程依赖于增益计算流程。

2.滤波状态和测量初值选取

卡尔曼滤波是一种递推算法，启动时必须先给定初值X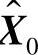和P₀。如果选取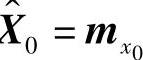，则滤波过程中估计始终无偏，即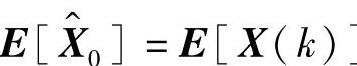。如果开始并不了解初始状态的统计特性，令

式中，α为很大的正数，在此情况下滤波器不能保证是无偏的。由于P₀≠C_X0，所以实际的估计均方误差也不一定是最小的。如果系统是一致完全随机可控和一致完全随机可观测的，则卡尔曼滤波一定是一致渐进稳定的。即随着滤波步数的增加，盲目选取的滤波初值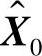和P₀的影响将逐渐减弱直至消失，估计逐渐趋向无偏，估计的均方误差也逐渐和P₀=C_X0时的结果保持一致。