4.2.1.1 CNN的理论

CNN的基本运作单元称为“细胞”（Cell），也就是通常所说的神经元。用电路实现的时候，“细胞”包含线性和非线性电路器件。CNN定义其网络中的任一细胞仅与其邻域内的细胞相连。这些相连的细胞通过权重直接相互作用，非直接相连的细胞则通过网络的动力学传输效应间接相互作用。当前应用的绝大多数细胞神经网络为单层二维网络结构，在应对高复杂性的任务时也可采用多层网络结构。一个M×N的细胞神经网络是安排在M行N列的二维空间中的，第i行第j列用C_i，j表示，如图4.18所示。每个细胞以各自为中心，与一个半径为r的邻域内的其他细胞通过一个耦合定律相连，耦合关系由模板决定。需要说明的是，细胞虽然是空间离散的，但与之相关的各个变量却是时间连续的，即是模拟量。

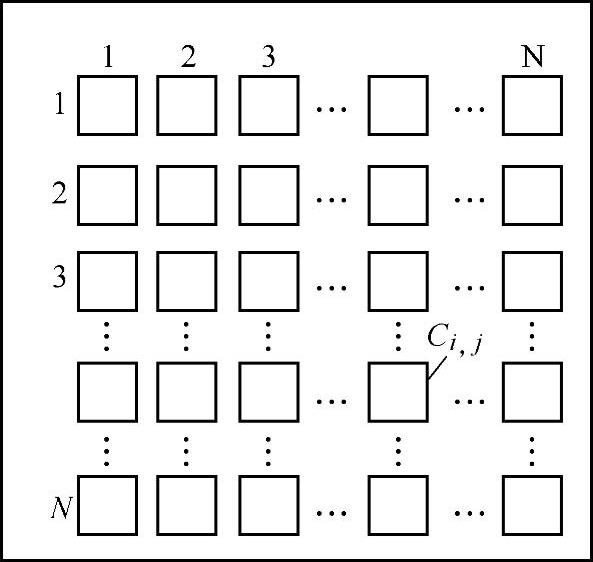
图4.18 标准的CNN结构

1.CNN的相关概念^[7]

（1）细胞

一般地，每个细胞都有以下4个变量：

1）输入（input）变量——u_i，j

2）阈值（threshold）——z_i，j

3）状态（state）变量——x_i，j

4）输出（output）变量——y_i，j

以上4个变量（阈值通常为常数）在一般情况下为连续时间t的函数。对于给定时刻t₀的状态变量x_i，j（t₀），阈值z_i，j（t₀），输入值u_i，j（t₀），每个细胞的状态变量依照以下“状态变量方程”变化：

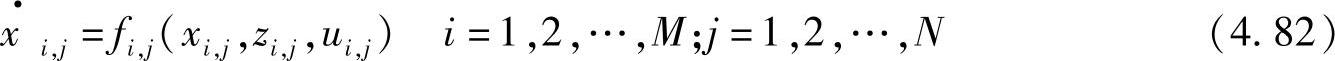
式中，f_i，j由式（4.82）确定。

（2）邻域（影响球）

给定整数r、k、l且r≥0，1≤k≤m，1≤l≤n，C_i，j为中心细胞。若N_r为网络中满足下式的所有细胞的集合，则称N_r为中心细胞C_i，j的r阶邻域（影响球），有

N_r（i，j）={c_k，l|max（|k-i|，|l-j|）≤r} （4.83）式中，r为半径，N_r（i，j）就是（2r+1）×（2r+1）的邻域。网络中每个神经元与周围r范围内的神经元相连。例如，r=1表示一个神经元除了与本身相连外，还与周围8个其他神经元相连；r=2表示与周围24个神经元相接；r=n则与（2n+1）²-1个其他神经元相连。一个二维细胞神经网络（r=1，r=2，r=3）如图4.19所示。通常，r=1（r=2；r=3）的邻域又称为3×3（5×5；7×7）的邻域。

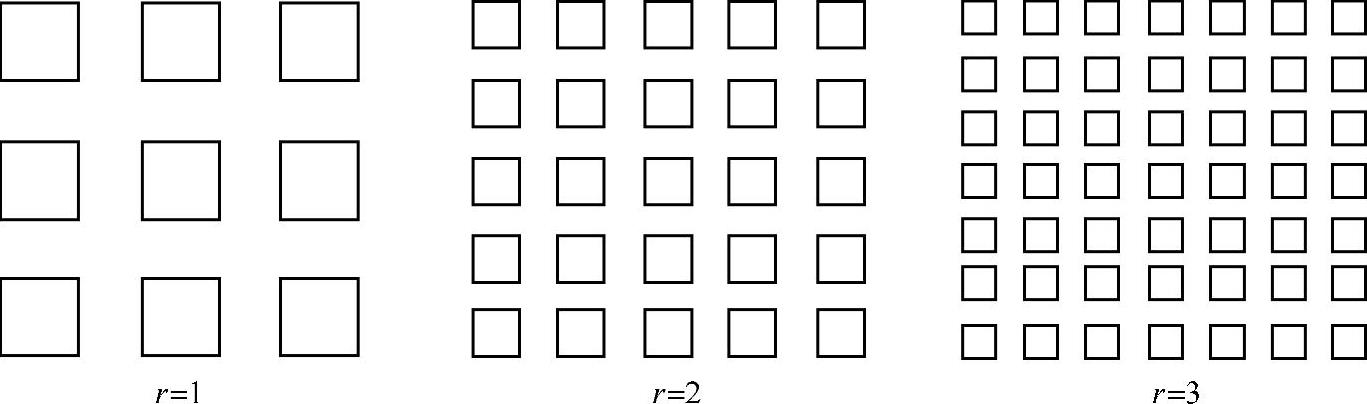
图4.19 （2r+1）×（2r+1）邻域CNN

（3）局部耦合性

在细胞C_i，j的r阶邻域之内的其他8个细胞，C_i+k，j+l（|k|≤1，|l|≤1）的输入量u_i+k，j+l，（|k|≤1，|l|≤1）的集合B（u_i，j）对C_i，j施加影响，有

由于u_i+k，j+l是外部信号，所以称b_k，l为控制轴突。在细胞C_i，j的r阶邻域之内的其他8个细胞C_i+k，j+l（|k|≤1，|l|≤1）的输出量y_i+k，j+l（|k|≤1，|l|≤1）的集合A（u_i，j）对C_i，j施加影响，有

由于y_k，l是细胞C_k，l自身产生的变量，所以称a_k，l为反馈轴突。当然，以上两个线性耦合规则也可由非线性函数替代。

（4）常规细胞、边界细胞和虚拟细胞

对于m、n、r给定的一个细胞神经网络，如果某一细胞的r阶邻域中不包含边界像素点，则称其为常规细胞，否则称为边界细胞（BoundaryCells）。任何细胞C_i，j，满足

|k-i|≤r，|l-j|≤r，且k∉{1，2，…，m}或l∉{1，2，…，n} （4.86）称为虚拟细胞（VirtualCells），相应的x_i，j，y_i，j，u_i，j，z_i，j称为虚拟状态，虚拟输出，虚拟输入和虚拟阈值。

（5）边界条件和初值

细胞神经网络的运算形式为邻域运算，因此边界细胞的处理不同于常规细胞。不同之处在于，边界细胞的邻域存在空位，运算时需要将这些空位填充。填充方式称为边界条件，边界条件是细胞图像算子不可缺少的一部分，通常有以下三类边界条件：

1）定值（Fixed）边界条件

左虚拟细胞：y_i，0=α₁，u_i，0=β₁，i=1，2…，M

右虚拟细胞：y_i，N+1=α₂，ui_，N+1=β₂，i=1，2…，M

上虚拟细胞：y_0，j=α₃，u_0，j=β₃，j=1，2…，N

下虚拟细胞：y_M+1，j=α₄，u_M+1，j=β₄，j=1，2…，N

其中，α_i和β_i是给定的常数（通常给定为0）。

2）无流（Zero-Flux）边界条件

左虚拟细胞：y_i，0=y_i，1，u_i，0=u_i，1，i=1，2…，M

右虚拟细胞：y_i，N+1=yi，N，_ui，N+1=u_i，N，i=1，2…，M

上虚拟细胞：y_0，j=y_1，j，u_0，j=u_1，j，j=1，2，…，N

下虚拟细胞：y_M+1，j=y_M，j，u_M+1，j=u_M，j，j=1，2…，N

3）周期（Periodic）边界条件

左虚拟细胞：y_i，0=y_i，N，u_i，0=u_i，N，i=1，2…，M

右虚拟细胞：y_i，N+1=y_i，1，u_i，N+1=u_i，1，i=1，2…，M

上虚拟细胞：y_0，j=y_M，j，u_0，j=u_M，j，j=1，2…，N(www.daowen.com)

下虚拟细胞：y_M+1，j=y_1，j，u_M+1，j=u_1，j，j=1，2…，N

另外，还必须给每一个细胞定义初值x_i，j（0）。

总之，细胞神经网络由两个数学要素所组成：

1）由被称为细胞的连续非线性动力系统的空间离散集合而成，其中每个细胞通过输入变量，初始态和阈值来加载信息；

2）每个细胞以各自为中心，与一个半径为r的影响球范围内的各个细胞通过一个耦合定律相连。

2.CNN的数学模型

给定二维m×n细胞神经网络，称位于网络中第i行第j列的细胞为C_i，j。标准CNN的状态方程为^[7]

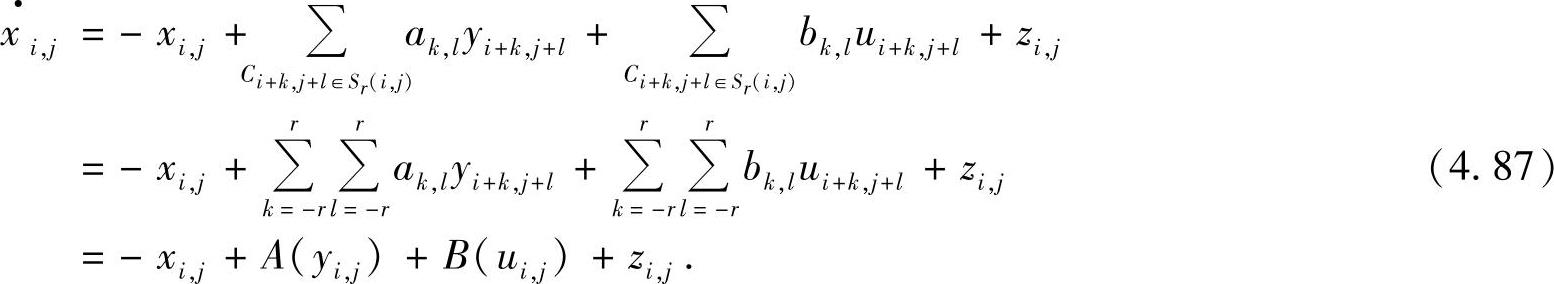
标准CNN的输出方程为

上述方程称为标准非线性方程，如图4.20所示。其中，x_i，j，y_i，j，u_i，j，z_i，j为标量，分别称为状态，输出，输入，和阈值。参数r称为影响球半径。其中参数a_k，l，b_k，l对应于CNN功能实现电路中相应的A模板和B模板（见表4.7，表4.8）。这是CNN研究及其特征表现的核心。适当地选择CNN参数，可以产生奇妙的图像处理功能。

图4.20 标准非线性输出函数

表4.7 r×rCNN的A模板

表4.8 r×rCNN的B模板

4.2.1.2 CNN在图像处理领域的应用

1.CNN的图像处理原理与步骤

CNN在简化网络结构的同时，依然保留了神经网络完全并行运算的优点。CNN处理图像的过程是整个网络所有细胞同时演化并趋向稳定的过程，是一个动态的并行处理的过程。作为一种面向集成电路实现的神经网络，CNN将并行计算和并行结构集于一身，并且具有与人眼视网膜相似的结构，因此用CNN来探索视觉计算和实时图像处理及解决当前图像处理领域存在的问题有着重要意义。利用CNN还可以完成边缘探测、轮廓线探测、连通性探测、对角线探测、腐蚀与膨胀、投影等任务。

近些年来，CNN研究取得了很大发展，并在图像处理和模式识别等方面取得了较好结果。目前，CNN已经广泛应用于图像处理水平线检测、垂直线检测、噪声移去、边缘提取、空洞填充、运动检测、特征检测和字符识别等诸多领域。利用CNN进行图像处理的应用研究已经很成熟。

（1）基于CNN的图像处理原理

1988年Chua和Yang首次提出CNN时就将其应用于图像处理^[6]，并成为CNN的典型应用领域。下面以灰度图像为例，说明CNN进行图像处理的原理^[28]。

设U=（u_i，j）∈R^M×N（其中|u_i，j|≤1），表示输入的初始图像；设

R^M×N，表示输出的最后处理图像。则所谓的数字图像处理过程就是这样的一个映射：

F：U→Y （4.89）

CNN图像处理的基本功能就是将一个输入图像映射成一个相应的输出图像，如图4.21所示。

从数学上说，CNN方程式（4.87）中的u_i，j表示输入初始图像U中第（i，j）个像素的灰度值；给定一个初始条件X（0）=（x_i，j）_M×N后，CNN方程的平衡点y_i，j（∞）对应于该CNN方程处理图像U的结果。

对标准的CNN方程而言，选择恰当的A、B模板，把初始图像作为CNN的输入量，选择合适的状态方程的初始条件和边界条件，则可把CNN的稳定输出Y（∞）=（y_i，j（∞））_M×N作为最终的图像处理结果。

图4.21 CNN图像处理原理图

（2）CNN图像处理的一般步骤

在处理图像过程中，一个CNN细胞对应一个数字图像处理的像素点，其中每一个细胞是一个复杂的动力系统。CNN处理图像的通常步骤如下：

1）选择恰当的CNN模型，如标准CNN、离散CNN、模糊CNN等，将数字图像的每一个像素看成局部耦合的CNN细胞；

2）通过分析数字图像处理所要达到的目标建立适当的局部规则；

3）通过建立起来的局部规则，使用一定的方法构造CNN处理数字图像的模板；

4）用计算机模拟观察构造的模板产生的图像处理效果，看构造的模板是否能满足要求；

5）对处理的图像效果尽可能地给出理论上的证明；

6）比较该CNN模板处理该图像与其他方法处理图像的优缺点。

2.CNN在图像边缘检测中的应用

CNN是一种只有最邻近的神经细胞元才进行通信连接的神经网络，这种神经网络模型能够对二维图像进行有效处理。近年来，CNN技术由于其可并行计算性和便于硬件实现等优势，获得了长足的发展。

CNN在黑白与彩色图像处理中的应用已经实现，并且仿真结果表明用CNN处理图像的效果理想。CNN在二值图像和灰度图像边缘检测中的应用研究已经比较成熟。CNN做彩色背景置换等其他的彩色图像处理也已经应用。而CNN在彩色图像边缘检测中的应用研究现在还是空白，而现实中的图像很多是彩色的，因此，很有必要提出一种新的CNN模板，实现彩色图像边缘检测的功能。为了扩展其应用领域，需要对CNN在彩色图像边缘检测中的应用进行研究。