对于反对称双正交小波变换，在小波重构过程中提取图像的边缘信息，为图像增强提供了一种有效的途径。其创新之处在于将图像增强融于小波多尺度塔式分解数据的重构过程之中，为图像的滤噪增强提供了一种崭新的思路。下面对此进行实验研究，假设噪声为高斯噪声，采用韩国学者Li Kyu Eom提出的基于混合高斯模型的小波域图像滤噪方法[4]对图像小波分解各分量滤噪，然后进行重构增强恢复。

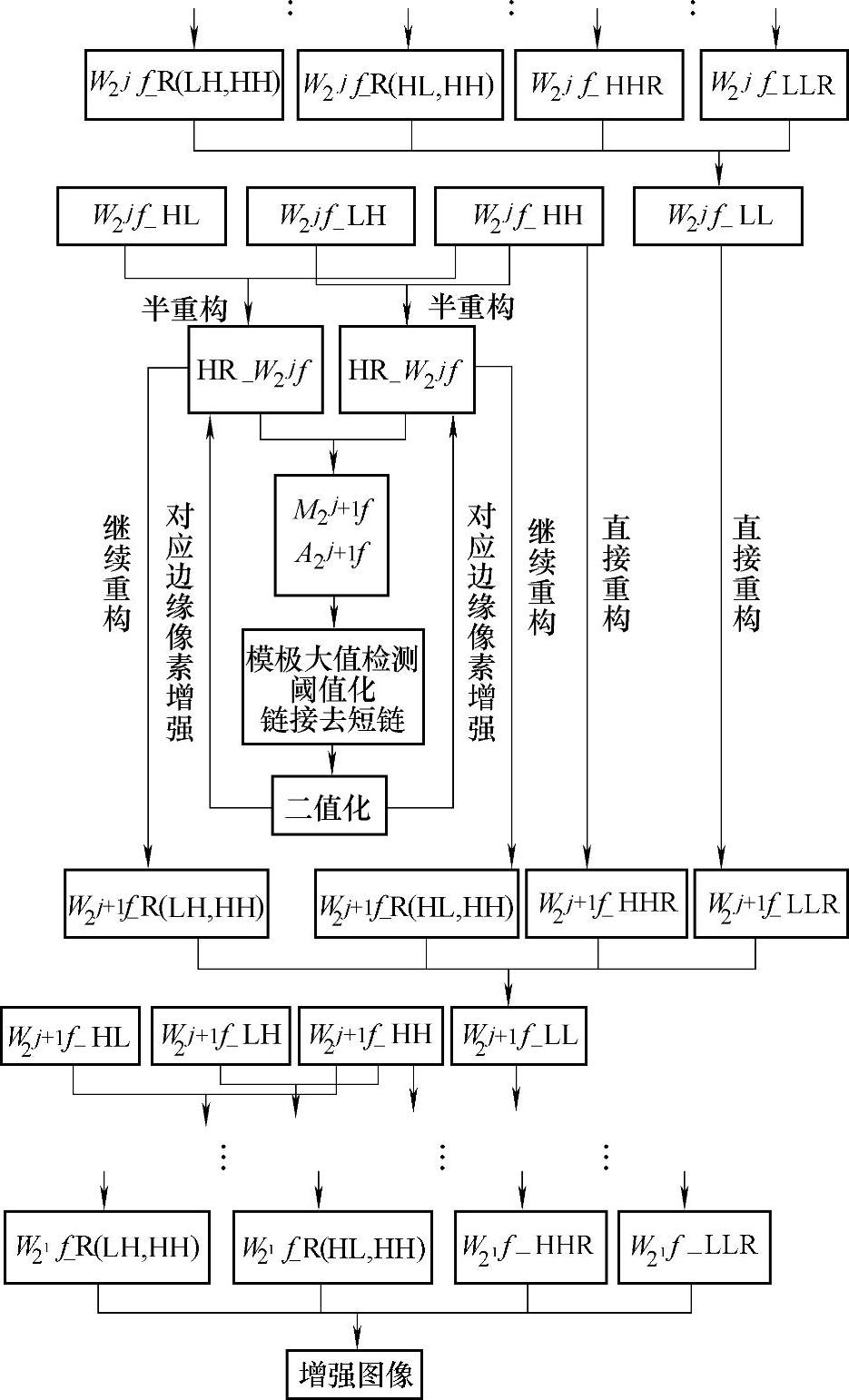
图4.6 反对称双正交小波重构增强示意图

4.1.4.1 基于混合高斯模型的小波域图像滤噪方法

1.图像建模

将染噪图像描述为如下形式：

y（i，j）=x（i，j）+ε（i，j），i，j=1，…，P （4.69）

式中，y[i，j]为采集的实际图像；x[i，j]为未知的原始图像；ε[i，j]是具有零均值和确定方差σ²_n的高斯白噪声，滤噪的目的是通过技术方法从染噪图像y[i，j]中恢复x[i，j]。

基于小波变换的图像滤噪方法首先要采用双通道滤波器，对图像y[i，j]进行多尺度小波变换，设

Y[^s，o][i，j]，i，j=1，…，P/2^s表示一定尺度下不同方向的小波系数。o∈{HL，LH，HH，LL}。设X[^s，o][i，j]和E[^s，o][i，j]分别代表原始图像x[i，j]和噪声图像ε[i，j]的小波系数。

由分解的小波系数可以看出，每一尺度细节分量的小波系数X[^s，o][i，j]是独立的高斯变量，对小波系数作如下最小均方误差（Minimum Mean Square Error，MMSE）估计：

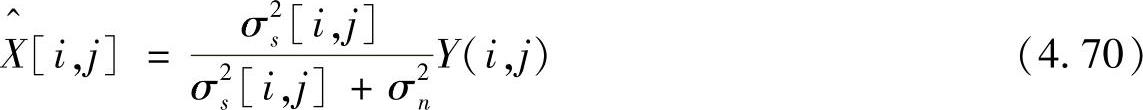
这里假设σ²_s[i，j]是确定的和已知的，但实际上σ²_s[i，j]是未知的。因此，需要对σ²_s[i，j]进行估计，设σ²_s[i，j]的估计量是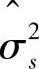[i，j]。对小波系数X[^s，o][i，j]的估计取决于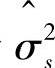[i，j]的准确程度。

2.小波分解系数的二值化

将小波系数分为显著小波系数和不显著小波系数两类，首先采用自适应阈值形成小波系数X[i，j]的二值编码m[i，j]，自适应阈值为

二值化的小波系数二值编码如下：

显著小波系数代表图像中的边缘和纹理，不显著小波系数代表图像中的平坦区域。图4.7所示为多尺度分解的二值化后的小波系数。

3.混合高斯模型

设高频小波系数是线性相关的高斯随机变量，二值化后的小波系数编码m[i，j]=1的小波系数服从零均值、高方差的高斯分布，即

f（X[i，j]|m[i，j]=1）=g（X[i，j]∶0，σ²₁[i，j]）

（4.73）(www.daowen.com)

式中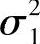，[i，j]为显著小波系数的方差；g（·）为高斯密度函数。同理，二值化后的小波系数编码m[i，j]=0的小波系数服从零均值、低方差的高斯分布，即

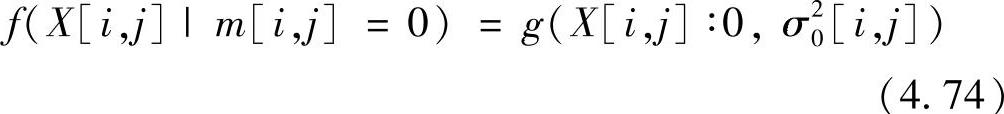
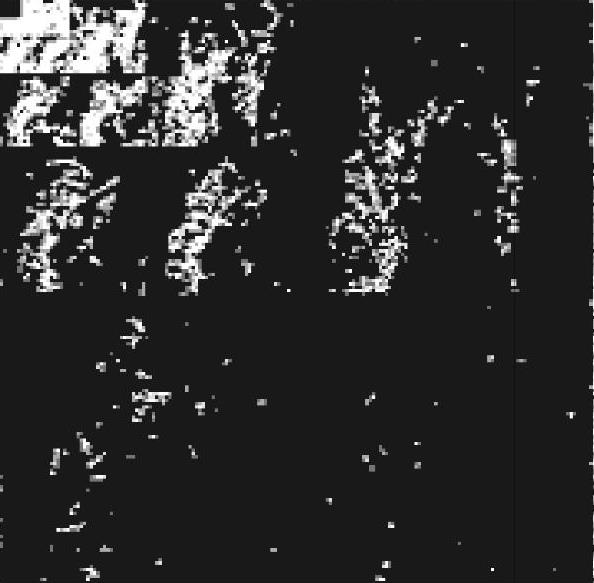
图4.7 二值化后的小波系数

由于σ²₁[i，j]>σ²₀[i，j]，小波系数的概率密度函数f（X[i，j]）由条件高斯分布得到

式中，p₀[i，j]和p₁[i，j]分别是显著和非显著小波系数的概率，并且p₁[i，j]=1-p₀[i，j]。

4.参数估计

上述高斯混合模型的参数为{p₁[i，j]，σ₀²（i，j），σ²₁（i，j）}。显著小波系数概率的计算采用小波系数X[i，j]邻域的平均值计算，即

式中，c₁（i，j）是X[i，j]邻域小波系数的集合；|c₁（i，j）|是c₁（i，j）中小波系数的数量。局部方差的估计是根据其邻域窗口的小波系数得到的。根据高斯密度函数的最大似然估计，得到

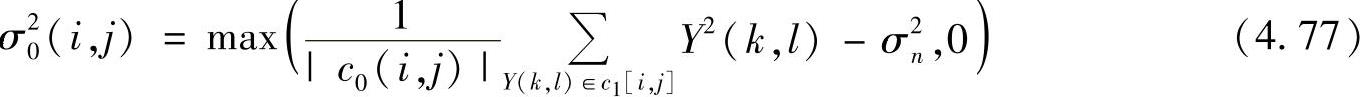
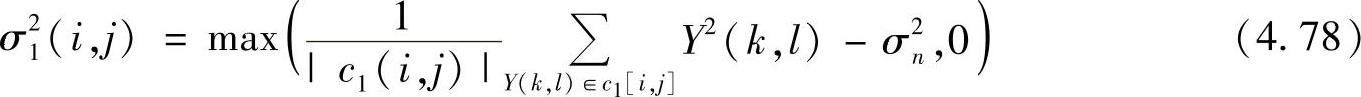
式中，c₁（i，j）是邻域小波系数集合；|c₁（i，j）|是c₀（i，j）中的小波系数的数量。根据前述小波变化的特点，小波系数按四叉树结构传播，如果上一级小波系数较小，则下一尺度相似位置的小波系数也较小。根据这一特点，得到最后的局部方差估计为

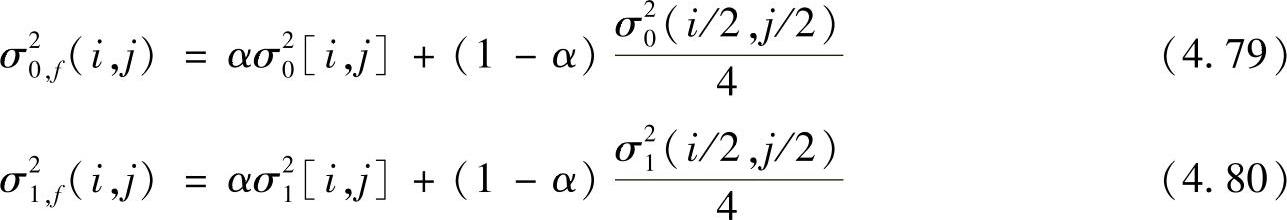
式中，α是加权因子。最后采用小波系数邻域内的维纳滤波估计小波系数为

4.1.4.2 基于反对称双正交小波重构的图像滤噪增强恢复

对图像进行多级小波分解后，针对不同性质噪声，采用新的或比较成熟的滤噪方法对塔式小波域数据作滤噪处理，然后在重构中对图像进行增强。其算法流程如图4.8所示。这种特点尤其适合于小波域滤噪后的图像恢复增强。任何小波噪声滤除方法在抑制噪声的同时，都不可避免地会造成图像中有用信息的损失，特别是高频信息。应用基于反对称双正交小波的图像增强方法，可以在小波域进行图像滤噪后，通过本书4.1.3中设计的小波重构算法，有目的地对图像边缘信息进行增强恢复，并进一步滤除噪声、复原并突出图像中的重要信息。这种图像增强思想通过反对称双正交小波重构将小波域滤噪方法和类似于二进小波的边缘检测方法巧妙地融合在一起，而这一切是在图像滤噪后的重构过程中完成的，不会增加额外计算量。这是基于反对称双正交小波重构的增强算法重要的应用价值之一。

图4.8 图像滤噪增强算法流程