1.相关知识
(1)理想小波函数性质
理想的小波函数应具有下列性质:①线性相位特性;②紧支集特性;③消失矩特性;④正则性特征。其中,小波函数具有线性相位,即小波函数具有对称性,可以避免或消除重构图像在边缘处的失真,保证对小波系数处理后函数的精确重构。
(2)小波运算形式
小波运算的形式有两种:相关型小波变换运算和卷积型小波变换运算。相关型小波变换运算通过函数与小波函数进行内积运算来实现。卷积型小波变换运算是指函数奇异性检测中的二进卷积型小波变换运算。相关运算的意义是求被分解函数与小波函数的相似程度,卷积运算的意义是用小波函数对被分解函数做卷积平滑滤波。
(3)反对称双正交小波与图像边缘提取
常用的基于小波变换的多尺度边缘提取方法,采用不具备正交性的二进卷积小波。在数值计算领域,更希望采用某种正交性小波多尺度塔式分解数据进行边缘信息处理。Mallat在有关文献中指出,用于边缘检测的小波函数ψ必须是反(奇)对称的;紧支集正交小波函数不具有对称性;双正交小波放宽了正交条件,可以构造出具有线性相位的紧支集小波。因此,反对称双正交小波具有边缘提取的能力。
(4)图像增强的小波基选取
图像增强小波基选取应满足平移不变性的要求,冗余小波变换是目前图像增强中常用的小波变换。双正交小波变换具有平移不变性,并可利用对称性避免边界效应。
基于上述知识,反对称双正交小波适合于对小波多尺度塔式分解数据进行边缘提取和图像增强。以下对反对称双正交小波所具有的卷积运算性质、微分算子功能和针对多尺度边缘提取三方面展开讨论。
2.反对称双正交小波的卷积运算性质
如果ψ(x)、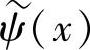 和φ(x)、
和φ(x)、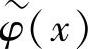 分别为L2(R)空间的双正交小波函数及其对应的尺度函数,ψ(x)是反对称的,则φ(x)必为偶对称。设Ψ(x)=ψ(-x)、
分别为L2(R)空间的双正交小波函数及其对应的尺度函数,ψ(x)是反对称的,则φ(x)必为偶对称。设Ψ(x)=ψ(-x)、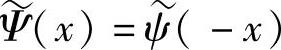 、Φ(x)=φ(-x)、
、Φ(x)=φ(-x)、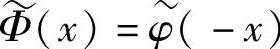 ,显然Φ(x)和Ψ(x)仍然是反对称小波函数和偶对称尺度函数。又设j尺度反对称双正交小波基函数为
,显然Φ(x)和Ψ(x)仍然是反对称小波函数和偶对称尺度函数。又设j尺度反对称双正交小波基函数为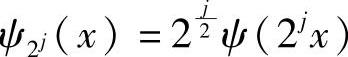 ,支集为[a,b],则中点为(b-a)/2,于是有
,支集为[a,b],则中点为(b-a)/2,于是有
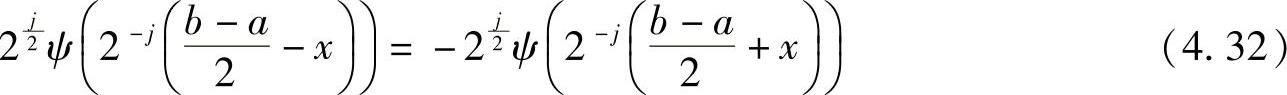
令x=x-(b-a)/2,于是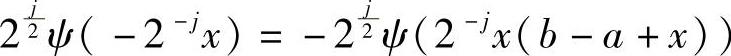 ,即
,即
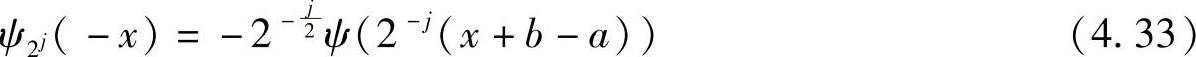
上式说明,对于反对称双正交小波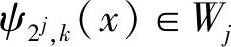 ,则
,则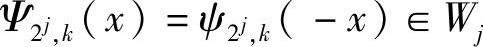 ,即
,即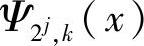 同样可构成Wj空间的一组Riesz基。类似地,
同样可构成Wj空间的一组Riesz基。类似地,
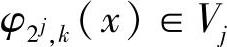
也有这种性质。根据两个多尺度空间的双正交条件,不难证明Ψ(x)、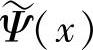 和Φ(x)、
和Φ(x)、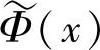 也可构成两个相同多尺度空间的双正交小波函数和尺度函数。双正交小波变换是相关型小波运算,即被分解函数与离散小波基函数做相关运算,对于实双正交小波变换有
也可构成两个相同多尺度空间的双正交小波函数和尺度函数。双正交小波变换是相关型小波运算,即被分解函数与离散小波基函数做相关运算,对于实双正交小波变换有
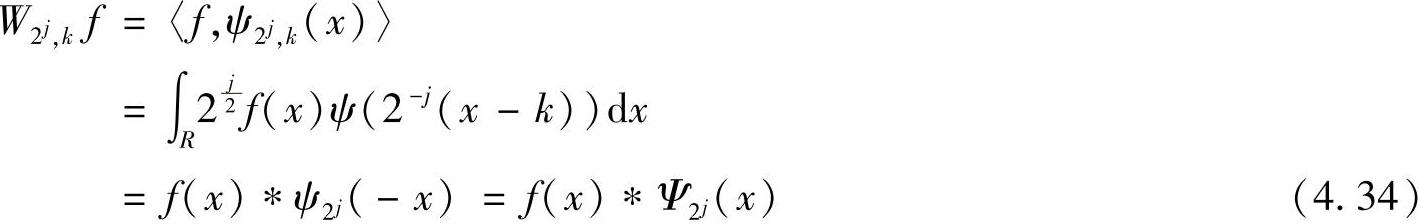
因此,对函数采用反对称双正交小波函数ψ(x)∈Wj做相关型小波变换,相当于采用反对称双正交小波函数Ψ(x)∈Wj做卷积型小波变换。对于反对称双正交小波及其相应的双正交尺度函数,则小波函数和尺度函数及其对偶小波函数和尺度函数有如下对应关系:
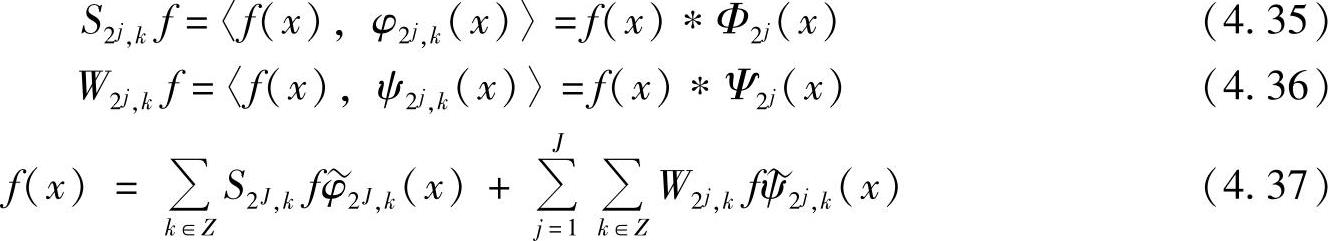
综上所述,反对称双正交小波变换具有卷积运算性质。当φ(x)、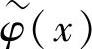 和ψ(x)、
和ψ(x)、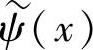 构成L2(R)空间的两个多尺度分析的双正交尺度函数和双正交小波函数时,Φ(x)、
构成L2(R)空间的两个多尺度分析的双正交尺度函数和双正交小波函数时,Φ(x)、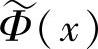 和Ψ(x)、
和Ψ(x)、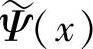 同样可构成这两个多尺度分析的双正交尺度函数和双正交小波函数。当采用ψ(x)和φ(x)做卷积型双正交小波变换时,其综合小波函数和尺度函数为
同样可构成这两个多尺度分析的双正交尺度函数和双正交小波函数。当采用ψ(x)和φ(x)做卷积型双正交小波变换时,其综合小波函数和尺度函数为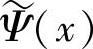 和
和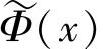 ,而不是
,而不是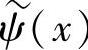 和
和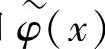 。
。
3.反对称双正交小波变换的微分算子功能
(1)反对称双正交小波变换的微分算子功能的频域证明[2]
令ψ(x)是一个具有反对称的双正交小波函数,θ(x)是ψ(x)的积分,即
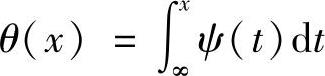
对此式两边进行傅里叶变换,并利用二尺度方程的频域表达式,可得
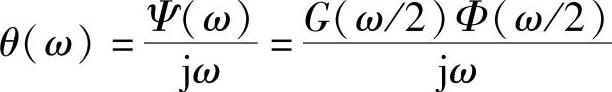
式中,Φ(ω)是和小波函数ψ(x)相对应的尺度函数φ(x)的傅里叶变换,ψ(x)满足
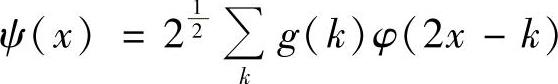
G(ω)定义为
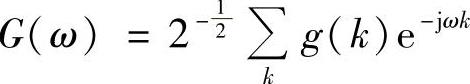
对于一个具备线性相位的反对称双正交小波而言,系数g(k)必须是偶数长度的反对称序列。不失一般性地,假设其对称点为-0.5,则g(k)满足
g(k)=-g(-1-k),k=0,1,…,n-1 (4.38)利用式(4.38),G(ω)可以写为
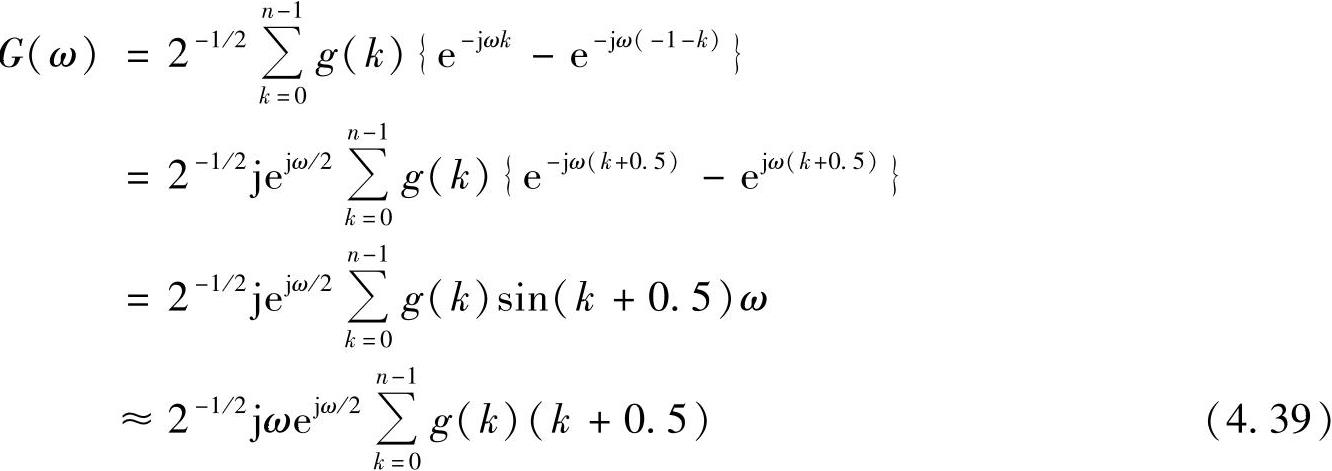
可得
θ(ω)≈ηejω/4φ(ω/2) (4.40)
式中,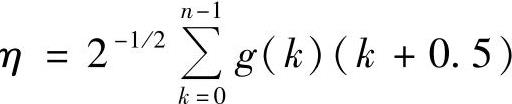 。由此得到
。由此得到
θ(x)≈ηφ(2x+0.5) (4.41)
上式表明,在一阶近似条件下,反对称双正交小波函数ψ(x)的积分θ(x)和尺度函数φ(2x)成比例关系。对于具有其他反对称点的小波函数,很容易得到类似结果。
以上结论对应用反对称双正交小波进行图像边缘检测具有重要意义。设f(x)为一个二次方可积函数,则其j级分辨率上的小波变换为

利用式(4.41),可得
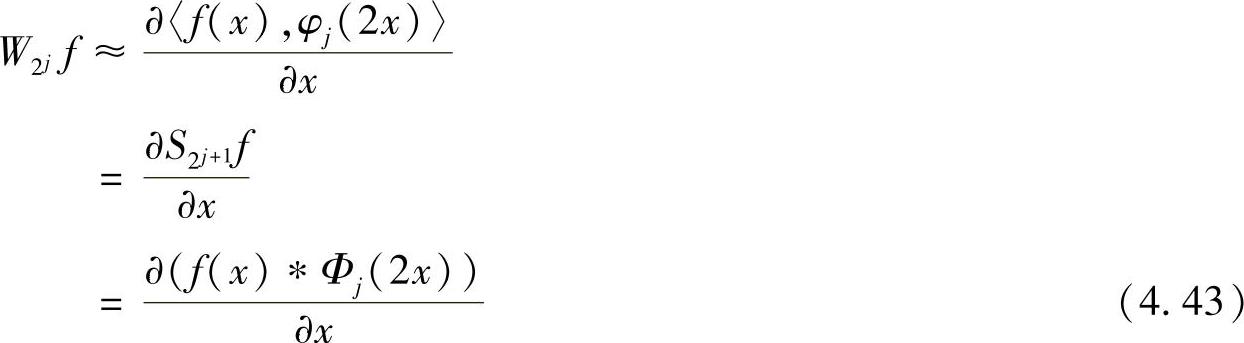 (https://www.daowen.com)
(https://www.daowen.com)
式中,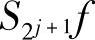 为f(x)在j+1级分辨率上的近似(卷积平滑)。式(4.43)表明,信号f(x)在j级分辨率上的小波变换
为f(x)在j+1级分辨率上的近似(卷积平滑)。式(4.43)表明,信号f(x)在j级分辨率上的小波变换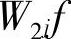 与该信号在j+1级分辨率上的近似(卷积平滑)成比例,因此W2jf的局部极值就对应了
与该信号在j+1级分辨率上的近似(卷积平滑)成比例,因此W2jf的局部极值就对应了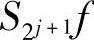 的剧烈变化点。
的剧烈变化点。
对二维信号f(x,y),当采用相关型小波变换时,则其j级分辨率上小波变换为
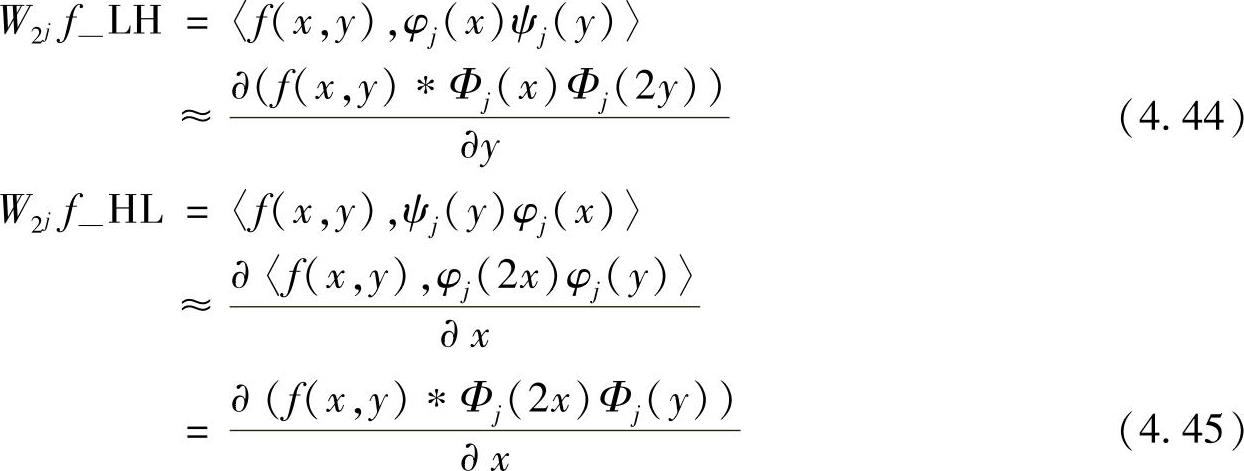
(2)反对称双正交小波变换的微分算子功能的时域证明[3]
由于紧支撑且具有线性相位的反对称双正交小波的二尺度系数序列hk和gk的长度必均为偶数,且两者相差为2的偶数倍,因此不失一般性地,可令gk的对称中心为0.5,长度为2K,起点下标为-K+1,终点下标为K,并且有
gk=-g1-k,k=0,1,…,K
考虑到
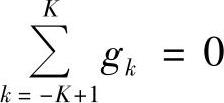
二尺度关系可重写为
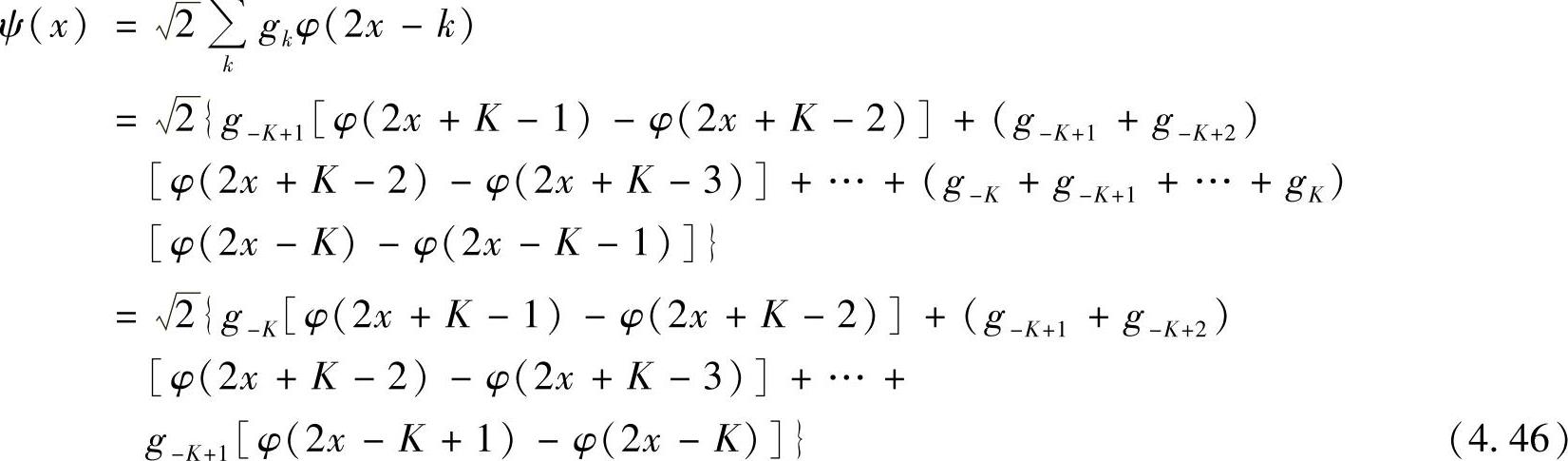
令上式的第k项系数为ck,则
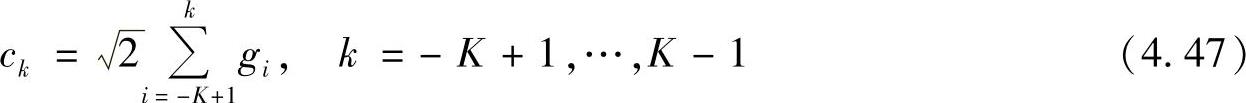
则ck是一个对称序列,有
ck=c-k,k=0,…,K
考虑到|gk|的值随|k|的增大而减小及在式(4.46)的求和中有正与负抵消,式(4.45)的各项中,以c0为系数的中间项将起主导作用。即ψ(x)可近似表示为
ψ(x)≈c0[φ(2x)-φ(2x-1)] (4.48)
如果φ(x)足够光滑,则根据中值定理,式(4.48)可进一步表达为
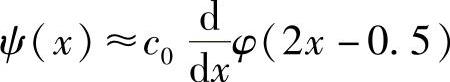
即任何紧支撑反对称双正交小波ψ(x)是近似地正比于高一级分辨率上与之相对应的尺度函数φ(2x)的导数。
4.反对称双正交小波重构过程中的多尺度边缘提取
反对称双正交小波变换具有卷积运算性质和微分算子功能,可以利用重构过程的中间结果,计算多个分辨率上近似图像的方向梯度的模值和相角值,进而进行边缘提取。这一功能的实现是在图像的重构过程中实现的。
相邻j+1和j尺度间的小波变换系数快速重构算法为
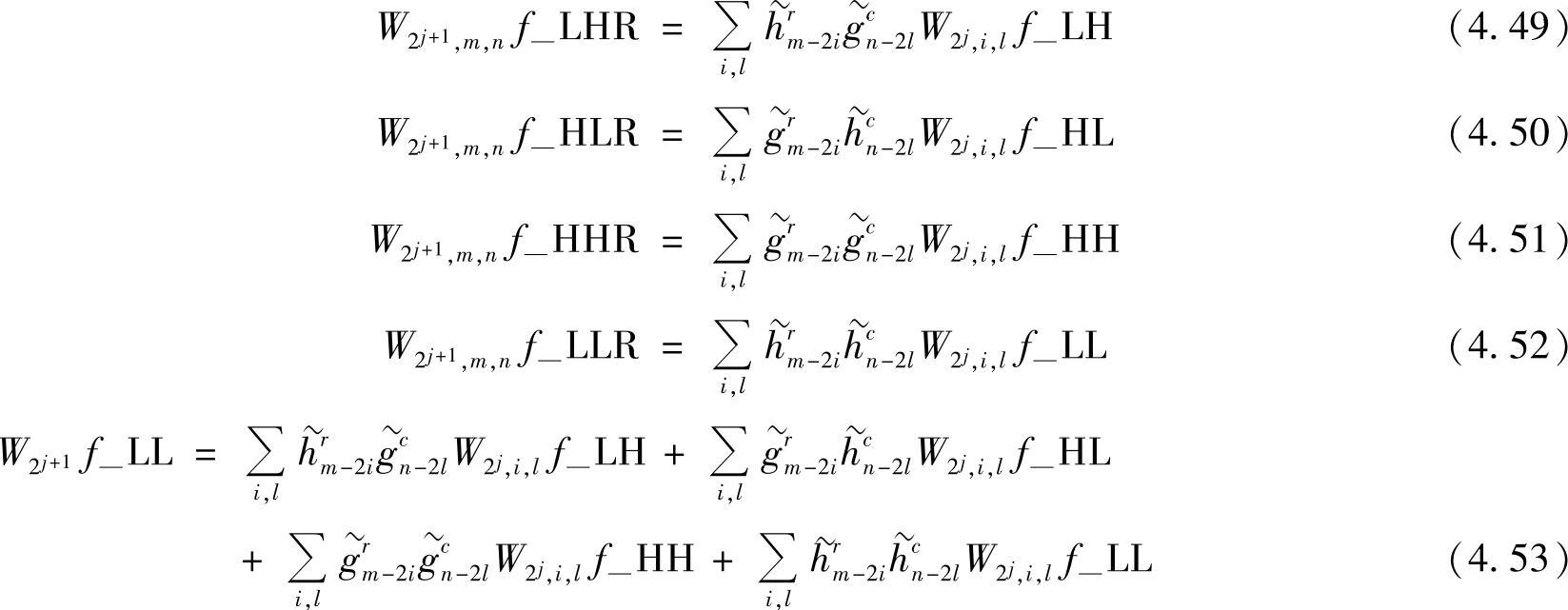
为了讨论问题方便,式(4.49)~式(4.53)可简写如下:
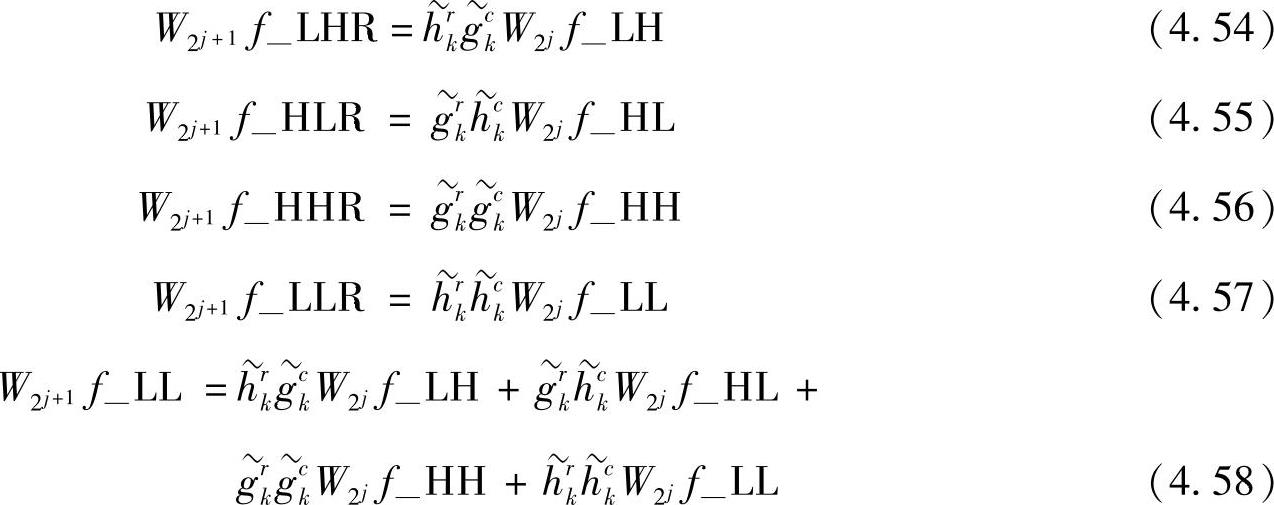
重新构造重构的式(4.58),有
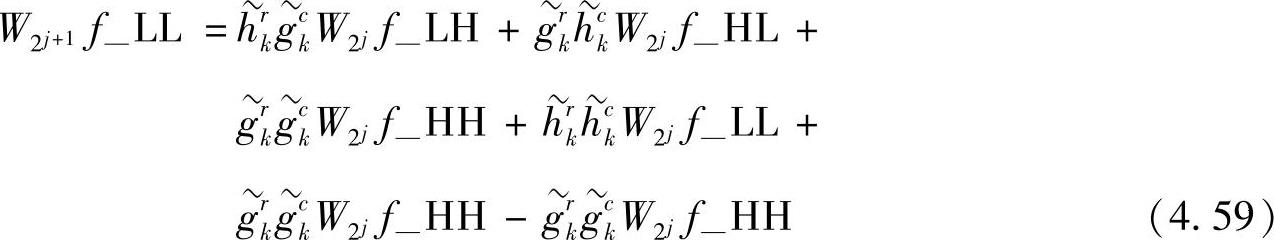
重新组合上述重构公式各项,有
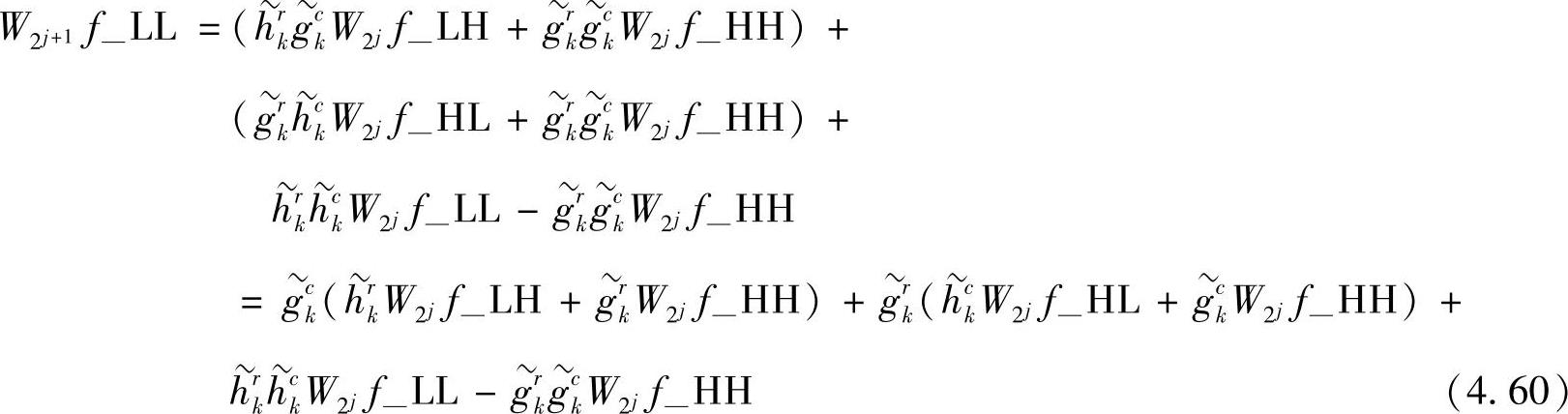
式(4.60)中(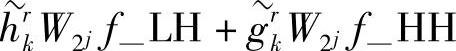 )是对W2jf—LH和W2jf—HH的每一行采用综合滤波器
)是对W2jf—LH和W2jf—HH的每一行采用综合滤波器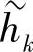 和
和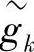 进行一维重构的结果,即
进行一维重构的结果,即
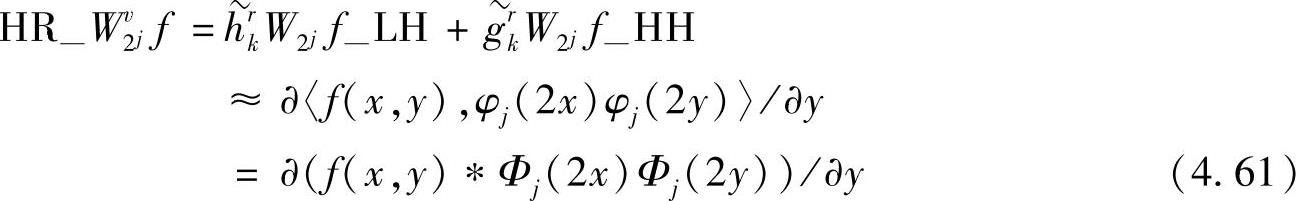
式(4.60)中(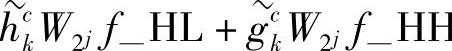 H)是对W2jf_HL和W2jf—HH的每一列采用综合滤波器
H)是对W2jf_HL和W2jf—HH的每一列采用综合滤波器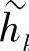 k和
k和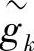 进行一维重构的结果,即
进行一维重构的结果,即
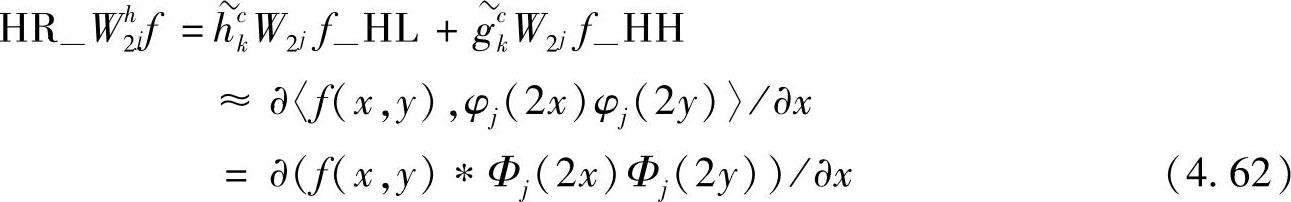
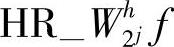 和
和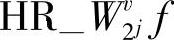 称为半重构,分别与j+1分辨率上近似分量水平方向和垂直方向的一阶导数成比例。在半重构的基础上,按照式(4.60)步骤继续重构形成j+1级分辨率近似分量。图4.4、图4.5所示为这一重构过程的电路结构示意图和过程示意图。
称为半重构,分别与j+1分辨率上近似分量水平方向和垂直方向的一阶导数成比例。在半重构的基础上,按照式(4.60)步骤继续重构形成j+1级分辨率近似分量。图4.4、图4.5所示为这一重构过程的电路结构示意图和过程示意图。
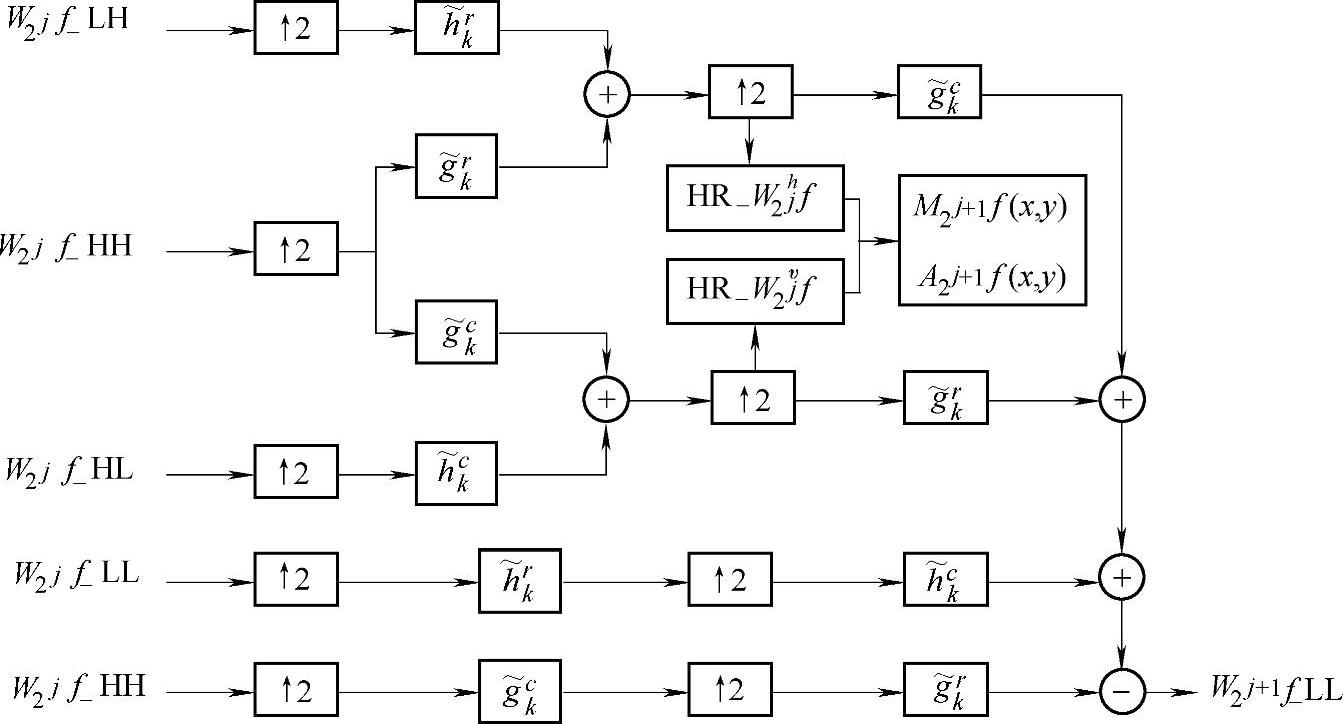
图4.4 针对图像边缘提取的二维小波重构电路结构示意图
重构过程多了两个j级分量的重构。由于进行了上采样,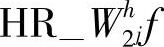 和H
和H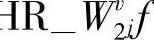 的大小与
的大小与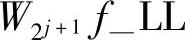 是一致的。根据小波半重构
是一致的。根据小波半重构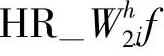 和
和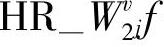 可以计算出j+1级分辨率上近似分量的模值和相角值。由于
可以计算出j+1级分辨率上近似分量的模值和相角值。由于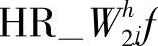 f和
f和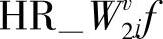 是由j级分辨率上的数据分别经过行重构和列重构并由上采样得到,因此在列方向和行方向上要比j+1数据低一个分辨率级,计算出的模值也低一个分辨率级。在小波分解数据上重复上述过程,能够计算出各级分辨率上的模值和相角值并最终重构图像。根据式(4.25)和式(4.26),二维信号f(x,y)在j+1级分辨率上近似分量
是由j级分辨率上的数据分别经过行重构和列重构并由上采样得到,因此在列方向和行方向上要比j+1数据低一个分辨率级,计算出的模值也低一个分辨率级。在小波分解数据上重复上述过程,能够计算出各级分辨率上的模值和相角值并最终重构图像。根据式(4.25)和式(4.26),二维信号f(x,y)在j+1级分辨率上近似分量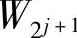 (f(x,y))—LL的梯度矢量可以表示为
(f(x,y))—LL的梯度矢量可以表示为
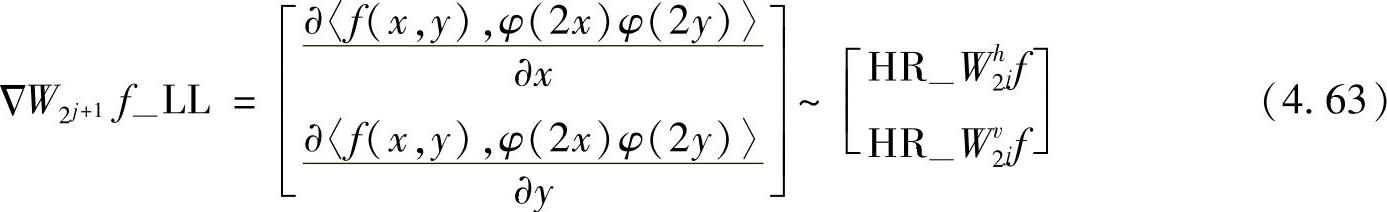
这样,可以直接基于反对称双正交小波的分解数据计算j+1级分辨率上的近似图像的方向梯度的模值M2jf(x,y)和相角值A2jf(x,y)。
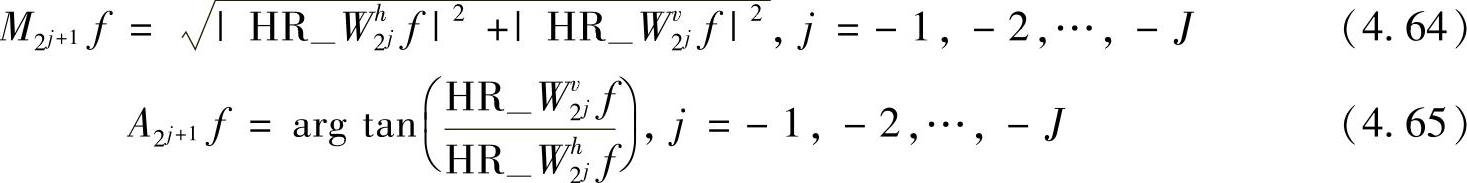
基于上述关系通过局部模极大值检测便可定位j+1级分辨率上的边缘像素点。在各级小波分解数据上重复上述过程,可得各个分辨率上近似图像的方向梯度模值和相角值。这种重构算法,将各分辨率上的边缘检测融入重构过程中,对图像增强有重要意义。
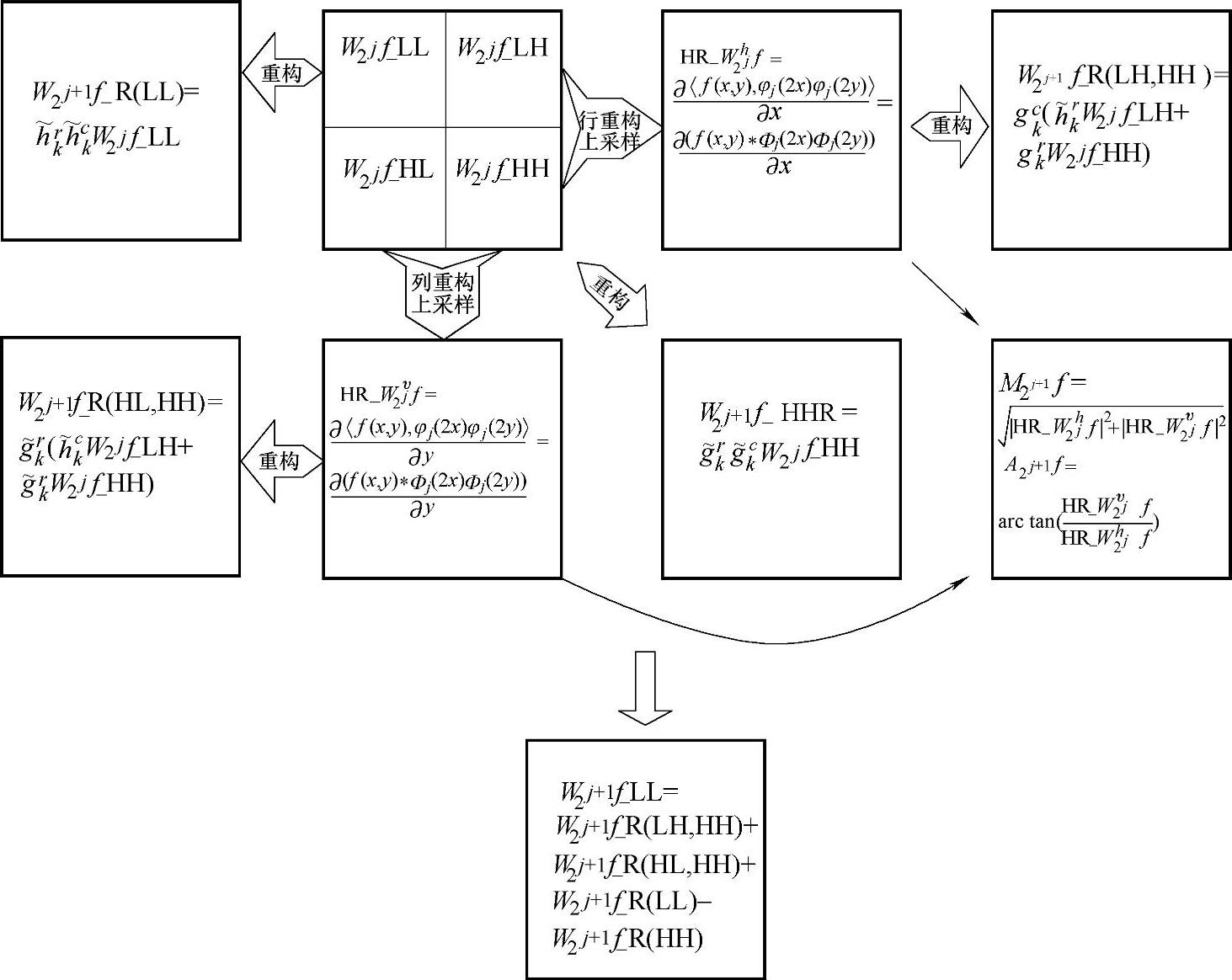
图4.5 针对图像边缘提取的二维小波重构过程示意图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







