1.多分辨率分析

[定义1] 多分辨率分析是指满足下述性质的一系列闭子空间{V_j}j_∈Z：

1）一致单调性

…⊂V₂⊂V₁⊂V₀⊂V_-1⊂V_-2⊂…

2）渐近完全性

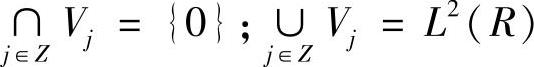
3）伸缩规则性

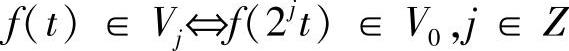
4）平移不变性

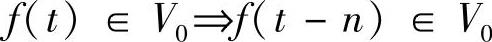
5）正交基存在性

存在φ∈V₀，使得{φ（t-n）}_n∈Z是V₀的正交基，即

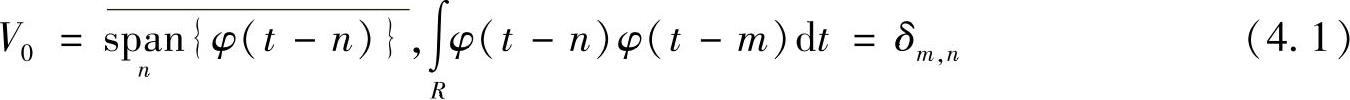
其中，正交基的存在性条件可放宽为Riesz（里斯）基存在性，由Riesz基可以构造出一组正交基。若{φ（t-n）}_n∈Z为空间V₀的正交基，则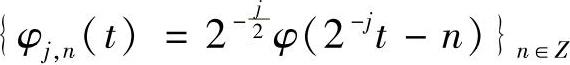必为空间V_j的标准正交基。所有闭子空间{V_j}_j∈Z都是由同一尺度函数φ伸缩后的平移系列张成的尺度空间，称φ（t）为多分辨率分析的尺度函数，其包含关系如图4.2所示。

多分辨率分析的一系列尺度空间是由同一尺度函数在不同尺度下张成的，即一个多分辨率分析{V_j}对应一个尺度函数。虽然有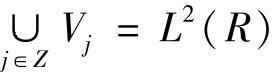，但由多尺度空间的定义可此，它们的基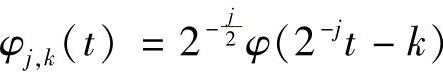在不同尺度间不具有正交性，即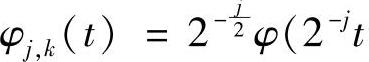-k）不能作为L²（R）空间的正交基。

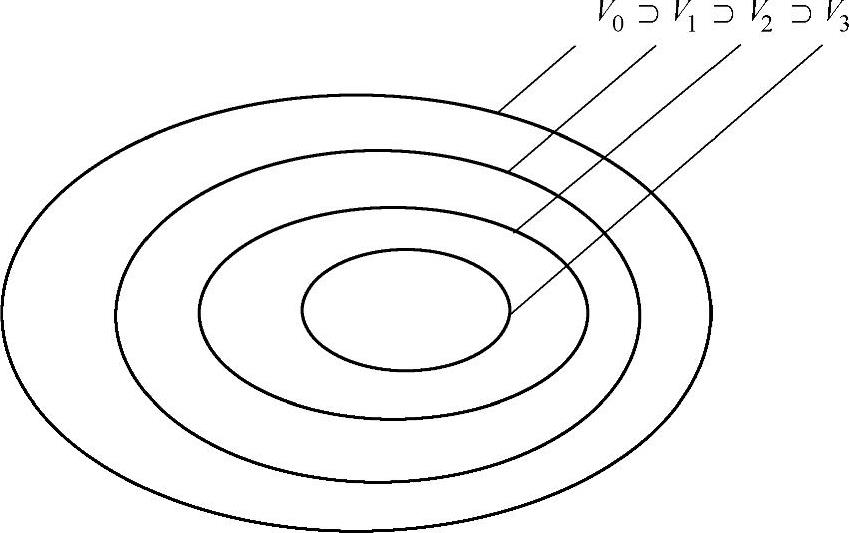
图4.2 闭子空间{V_j}_j∈Z相互包含关系

[定义2] 设W_m为V_m在V_m-1中的补空间，即

任意子空间W_m与W_n是相互正交的（空间不相交），W_m⊥W_n，m≠n，且有

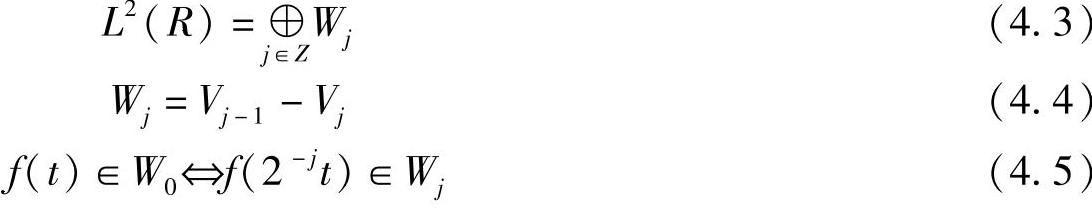
若设{ψ_0，k；k∈Z}为空间W₀一组正交基，则对所有的尺度j∈Z，有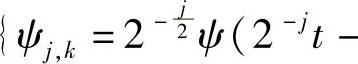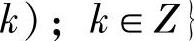必为空间W_j的正交基，ψ_j，k的整个集合必然构成了L²（R）空间的一组正交基。由知，{V_j}_j∈Z空间相互包含而不具有正交性。因于ψ_j，k是由同一母函数伸缩平移得到的正交基，故称ψ为小波函数，相应地称W_j是尺度为j的小波空间。如图4.3所示，小波空间是两个相邻尺度空间的差，相邻尺度空间的投影之间的细小差别即为函数f（x）在相应尺度小波空间上的投影，故小波空间也称为细节空间。

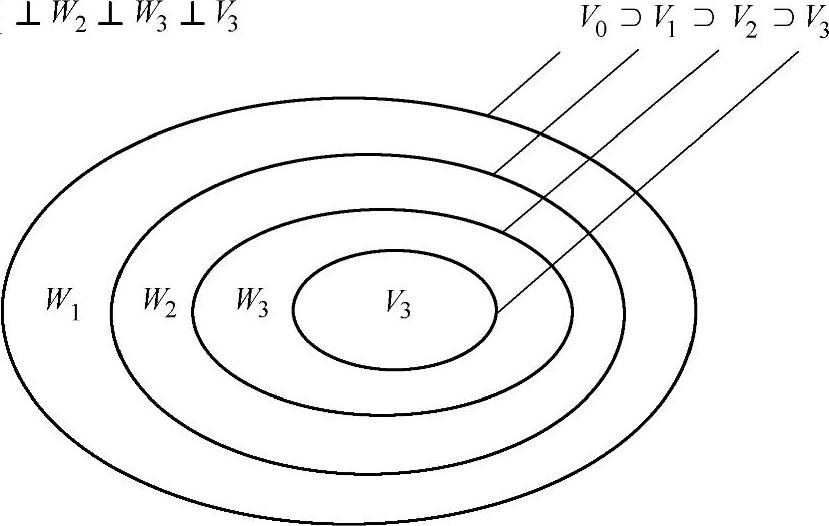
图4.3 小波空间示意图

2.紧支集双正交小波

定理：设φ（x）与ψ（x）是一个多尺度分析的紧支集正交实尺度函数和小波函数，且ψ（x）是对称或反对称的，则ψ（x）一定是Haar（哈尔）小波函数。

由上述定理可知，除Haar小波函数以外，紧支集、正交、对称的小波函数是不存在的。只有放弃正交性要求，才能满足紧支集和对称条件。

[定义3] 设L²（R）的两个多尺度分析有（{V_j}_j∈Z，φ（x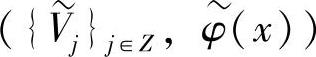）），。若

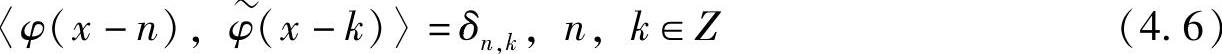
则称φ（x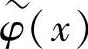）、是双正交尺度函数。从上述定义可知，双正交尺度函数要求两个不同的尺度分析的两个尺度函数之间有正交性。对同一尺度函数，不要求有平移正交性，构成一个多尺度分析的尺度函数不必是平移正交的。由多尺度分析的定义可得

函数系

是V_j的Riesz基，而函数系

(www.daowen.com)

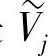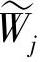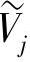是的Riesz基。设W_j是V_j在V_j-1中的补，是在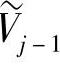中的补，则有

对于同一多尺度分析，不要求W_j与V_j正交、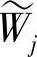与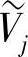正交。由双正交定义可知，

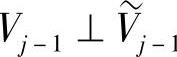于是可得

由此可得

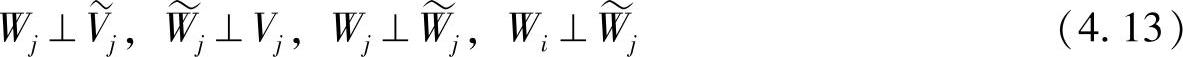
根据多尺度分析，有以下结论：

ψ（x）∈W_j⇔ψ（x-k）∈W_j （4.14）

ψ（x）∈W_j⇔ψ（2x）∈W_j-1 （4.15）对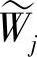也有这两个性质。由于式（4.14）、式（4.15）成立，所以若ψ（x）∈W₀，则{ψ（x_-k）}_k∈Z构成W₀的Riesz基，而函数系为

这样，就构成W_j的Riesz基。若ψ（x）∈W₀，则有

这样就构成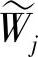的Riesz基。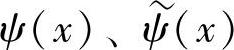称为双正交小波函数。双正交尺度函数与小波函数有下列二尺度方程：

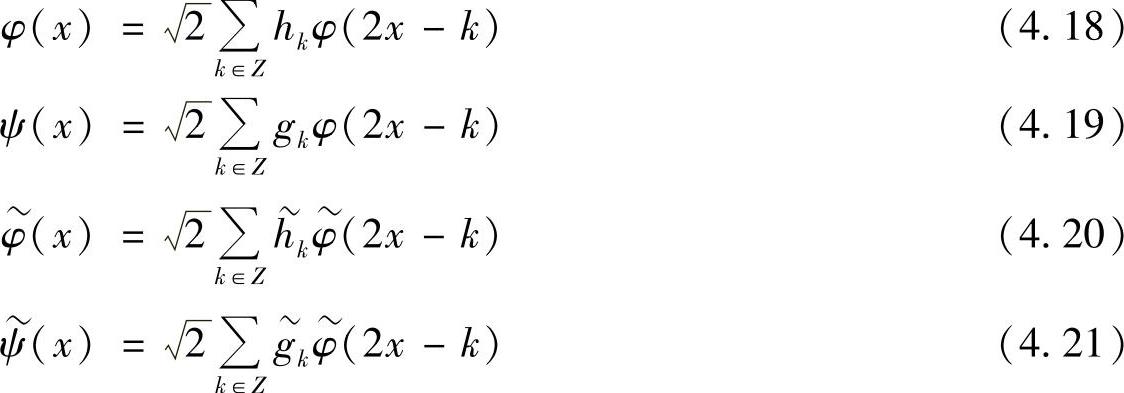
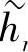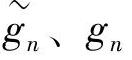与反对称双正交小波滤波器系数h_n、对应的为

由于{h_n}、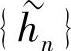中只有有限项非零，所以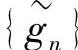、{g_n}中也只有有限项非零。可以证明，若h_n=h_-n，则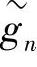是对称的；若h_n=h_1-n，则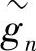是反对称的。

3.双正交小波变换的Mallat算法

与正交情形相似，在双正交情形下，也可用函数的多尺度逼近及其相应的快速算法。设（{V_j}_j∈Z，φ（x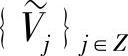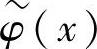））、（，）是L²（R）的两个多尺度分析，φ（x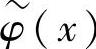）、满足式（4.6），ψ（x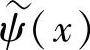）、是相应的双正交小波函数，则对任何J≥1，有

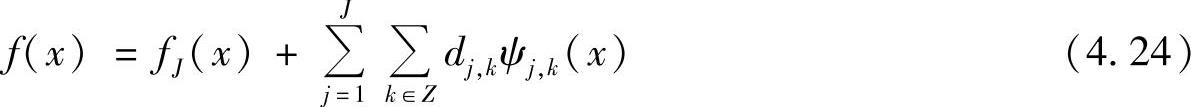
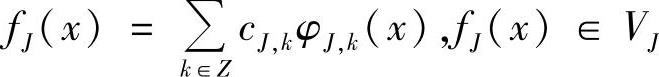是尺度J下f（x）的连续逼近，由式（4.24）得

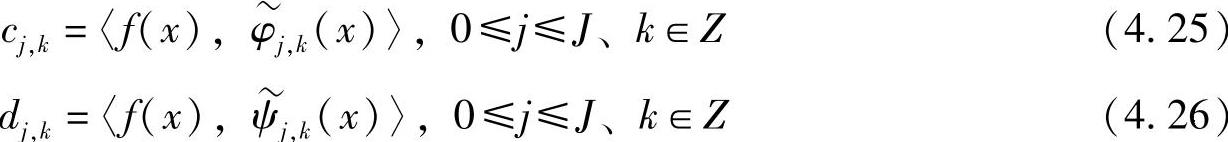
只要计算出c_j，k和d_j，k，就可得到f（x）在任何尺度下的连续逼近，即函数f（x）的多尺度逼近。由于L²（R）=…+W_-1+W₀+W₁+…，所以在式（4.24）中取|J|→∞，则可得

式中

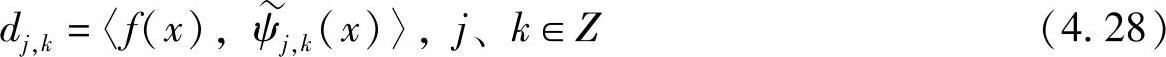
式（4.28）称为f（x）的双正交小波变换公式，式（4.27）称为双正交小波变换重构公式。可见，变换和重构是使用不同的小波函数进行的。以下是c_j，k、d_j，k的快速算法：

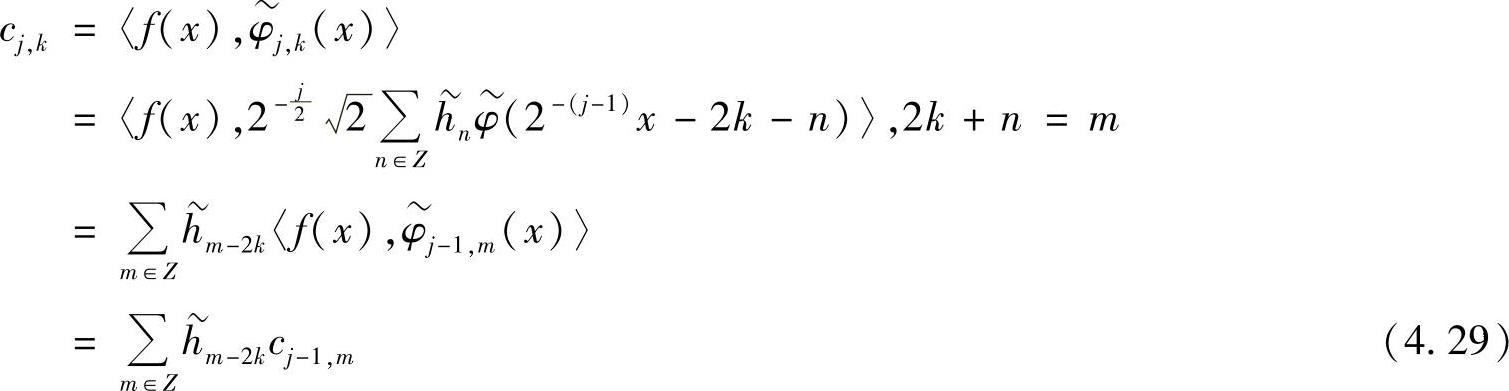
类似地

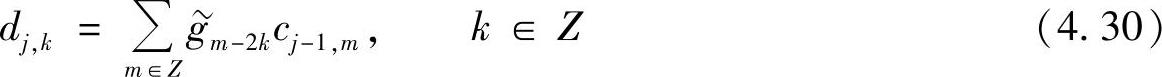
对于重构，有

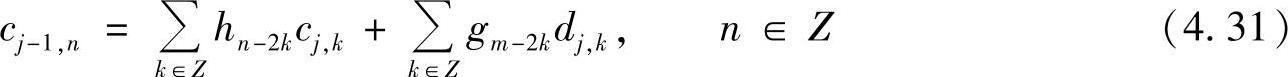
式（4.29）、式（4.30）称为双正交小波变换的Mallat算法分解公式，式（4.31）称为双正交小波变换Mallat算法的重构公式。可见，分解公式和重构公式是用两对不同的滤波器进行的。