图像增强是指按实际需要采取相应的技术手段强调图像中的某些特征而抑制其他信息，改善视觉效果，或使之更适合于图像的后续处理及特定应用过程。作为基本的图像处理技术，图像增强包含的内容比较广泛，广义上包括对比度增强，边缘、轮廓、纹理增强，图像锐化，噪声去除及几何畸变校正等。其中，图像对比度与灰度梯度相关，对比度的高低预示着灰度梯度的大小，边缘、轮廓和纹理增强也意味着对比度增强。根据具体应用目的的不同，图像增强方法主要有三类：空间域增强方法、变换域增强方法和基于参数优化的方法。其中，变换域增强方法是将图像变换到频域或小波域，对图像的变换系数进行某种修正，然后通过逆变换获得增强的图像，如基于傅里叶变换的同态增晰方法。

小波变换以其优异的时频域局部化和多分辨率分析能力在图像处理领域得到了广泛的应用。在现有文献中，小波域图像增强方法主要有两种：

1）小波变换反锐化掩模法，通过原始图像叠加原图与小波分解低频分量之差，实现边缘锐化；

2）小波变换高频增强法，即利用小波分解，将原始图像中高频分量和低频分量进行不同程度的分离，然后采用不同的方法来增强不同尺度的图像细节分量。

有文献证明小波变换高频增强法与小波变换反锐化掩模法有内在的联系。对小波分解后的高频通道乘以适当的增益，其结果类似于小波变换反锐化掩模法处理结果。

小波域图像增强往往和滤噪问题联系在一起，即滤噪和滤噪增强。滤噪的核心问题是在小波域数据区别噪声系数和图像边缘系数。对此，国内外学者做了大量的研究工作，提出了小波收缩法、小波模极大值法、相关性去噪法等滤噪法。小波收缩法分为比例收缩法和阈值收缩法。比例收缩法通过度量小波系数被噪声污染的程度，来确定系数收缩的比例。阈值收缩法通过选取适当的阈值，采用阈值函数压制小于阈值的小波系数来达到滤噪的目的。因此，阈值收缩法的研究重点是如何确定阈值和如何定义阈值函数。根据研究的侧重点不同，阈值分为统一阈值（全局阈值）和自适应阈值（局部阈值）两种。阈值函数主要有软阈值函数、硬阈值函数等。小波模极大值法采用二进卷积小波获得图像的模值图和相角图，通过利普希茨（Lipschitz）指数刻画信号的奇异性，利用信号和噪声在不同尺度模值图上的表现，利用模极大值原理进行滤噪，然后采用迭代实现交替投影法由模极大值点重构小波系数，这种方法计算量较大。相关性滤噪法是根据信号与噪声的小波变换系数在相邻尺度之间的相关性进行滤波的。

小波域滤噪增强一般是在辨识噪声系数和图像边缘系数的基础上，对不同的小波系数采取不同的拉伸策略，达到抑制噪声、增强有用信息的目的。类似地，考虑噪声情况的增强方法往往定义一个非线性的增益函数，使处于不同区间范围的小波系数得到不同程度的抑制或拉伸，来进行图像的抑噪增强。参考文献[1]中就研究了在一般小波变换情况下自适应选择映射函数进行增强和抑噪。

小波变换适用于表示各向同性奇异性的对象，但对于图像中具有线奇异和曲线奇异等高维几何特征的边缘、轮廓、纹理信息不能做到有效刻画和稀疏表示。因此，在图像处理领域很多学者致力于从构造具有方向选择性和各向异性并能对边缘进行稀疏描述的最优基函数的角度来解决问题。这就是多尺度几何分析方法。其中，针对图像滤噪和增强经常采用以Ridgelet变换、Curvelet变换和Contourlet变换为代表的非自适应几何分析。

上述方法是小波域图像滤噪和增强的主流方法。这些方法的共同特点是直接对小波分解数据进行处理，即在考虑噪声的基础上，对不同特点的小波系数进行剪裁和增强，然后通过小波重构改善图像效果，其算法的一般流程如图4.1所示。(www.daowen.com)

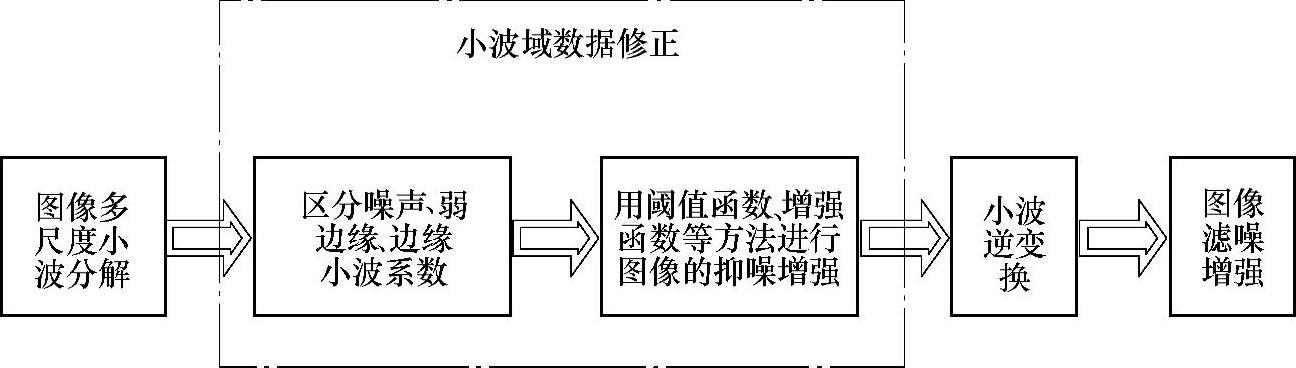
图4.1 小波图像滤噪增强算法一般流程

基于反对称双正交小波重构的图像增强方法首先对图像进行多尺度小波分解。然后，在小波重构中计算模值图和相角图，提取各尺度边缘图像。并且，根据边缘图像，来增强半重构图像的对应边缘点。最后继续逐级重构，实现图像增强。该方法在小波塔式分解数据的重构过程中，有针对性地实现对图像边缘的锐化增强，对于图像增强、图像的滤噪增强或图像滤噪后的复原问题，这种方法与上述小波域图像增强方法的思路不同，主要有如下特点：

1）在小波多尺度塔式分解数据上有针对性地实现对图像边缘的增强，比通常采用二进卷积小波实现图像边缘处理与增强减少了计算量；

2）针对图像边缘的锐化增强在小波重构过程中完成，不增加额外计算量，并优于小波域数据直接增强方法；

3）对于滤噪增强，先对小波多尺度塔式分解数据进行滤噪等处理，然后在小波逐级重构过程中提取图像边缘信息，进一步滤噪并增强边缘。

这一思想将小波域滤噪和边缘增强在多尺度塔式分解数据的重构过程中有机地结合在一起，对图像滤噪增强或图像滤噪后的复原提供了一种新的解决问题的思路。