设A是n阶矩阵,则A的特征值是方程|λE-A|=0(E是n阶单位矩阵)的根,而(λE-A)x=0的非零解是A的对应特征值λ的特征向量.
A的特征值与特征向量有以下性质:
(1)对应A的不同特征值的特征向量线性无关.
(2)A的特征值λ1,λ2,…,λn之和为trA,之积为|A|.
(3)设λ,ξ分别是A的特征值及其对应的特征向量,则f(A)有特征值f(λ)及其对应的特征向量ξ,其中f(λ)是λ的多项式.
(4)当A可逆时,A的特征值全不为零.设λ,ξ分别是A的特征值及其对应的特征向量,则A-1有特征值 及其对应的特征向量ξ;A∗有特征值
及其对应的特征向量ξ;A∗有特征值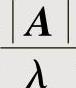 及其对应的特征向量ξ.
及其对应的特征向量ξ.
(5)设λ,ξ分别是A的特征值及其对应的特征向量,则P-1AP有特征值λ及其对应的特征向量P-1ξ.
利用特征值与特征向量的性质,往往能快捷地计算矩阵式的特征值与特征向量.
例11.1 设三阶矩阵A满足A-2E=0,A+2E=0,2A-3E=0(E是三阶单位矩阵),求A的行列式.
精解 由A-2E=0,即2E-A=0得2是A的特征值.
由A+2E=0,即-2E-A=0得-2是A的特征值.由2A-3E=0即23E-A=0得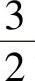 是A的特征值.
是A的特征值.
由此算得三阶矩阵A的3个特征值,所以
例11.2 已知二阶矩阵A及2维列向量x满足A2x+2Ax-3x=0,且x与Ax线性无关,求A的全部特征值与特征向量.
精解 由题设A2x+2Ax-3x=(A+3E)(A-E)x (E是二阶单位矩阵)
=(-3E-A)(x-Ax)
=(E-A)(-Ax-3x)
=0知,二阶矩阵A的特征值为λ=-3,1,并且由x与Ax线性无关知x-Ax≠0,所以对应λ=-3的特征向量为C1(x-Ax);同理可知-Ax-3x≠0,所以对应λ=1的特征向量为C2(-Ax-3x),其中C1,C2都是任意非零常数.
例11.3 设矩阵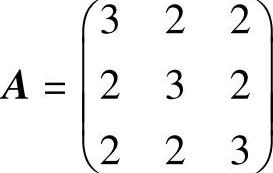 ,
,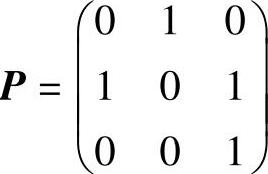 ,B=P-1A∗P,求B+2E的特征值与特征向量,其中A∗是A的伴随矩阵,E是三阶单位矩阵.
,B=P-1A∗P,求B+2E的特征值与特征向量,其中A∗是A的伴随矩阵,E是三阶单位矩阵.
精解 由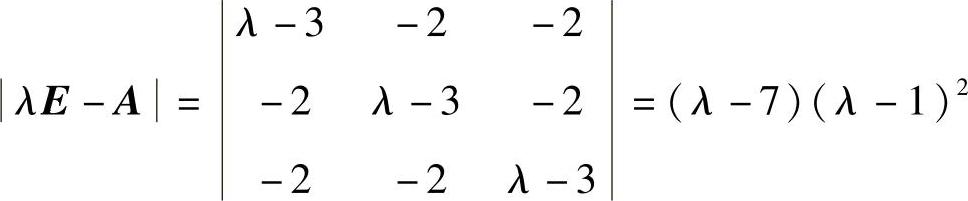 知A的特征值为λ=7,1(二重).
知A的特征值为λ=7,1(二重).
设对应λ=7的特征向量为α1=(x1,x2,x3)T,则α1满足
由于  所以,α1=C1(1,1,1)T=(C1,C1,C1)T(C1是任意非零常数).
所以,α1=C1(1,1,1)T=(C1,C1,C1)T(C1是任意非零常数).
设对应λ=1的特征向量为α2=(y1,y2,y3),则由A是实对称矩阵知
α2·α1=0, 即 y1+y2+y3=0,所以,α2=C2(-1,1,0)T+C3(-1,0,1)T=(-C2-C3,C2,C3)T(C2,C3是不全为零的任意常数).
于是A∗的特征值为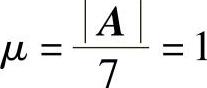 ,
,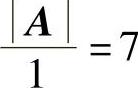 (二重)对应的特征向量分别为α1,α2.由此可得B的特征值为μ=1,7(二重),对应的特征向量分别为(www.daowen.com)
(二重)对应的特征向量分别为α1,α2.由此可得B的特征值为μ=1,7(二重),对应的特征向量分别为(www.daowen.com)
因此,B+2E的特征值ν=1+2=3,7+2=9(二重),对应的特征向量分别为
β1=C1(0,1,1)T,β2=C2(1,-1,0)T+C3(-1,-1,1)T.
例11.4 设矩阵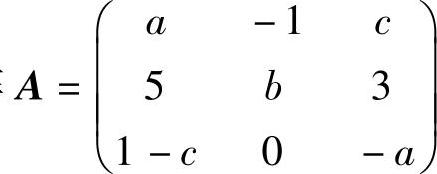 ,其行列式A=-1,又伴随矩阵A∗有一个特征值λ,属于λ的特征向量α=(-1,-1,1)T,求a,b,c,λ的值.
,其行列式A=-1,又伴随矩阵A∗有一个特征值λ,属于λ的特征向量α=(-1,-1,1)T,求a,b,c,λ的值.
精解 由题设可知,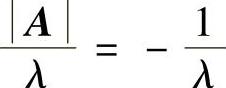 是A的特征值,其对应的特征向量为α,所以有
是A的特征值,其对应的特征向量为α,所以有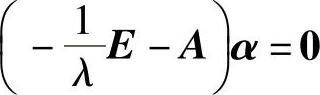 (E是3阶单位矩阵),即
(E是3阶单位矩阵),即 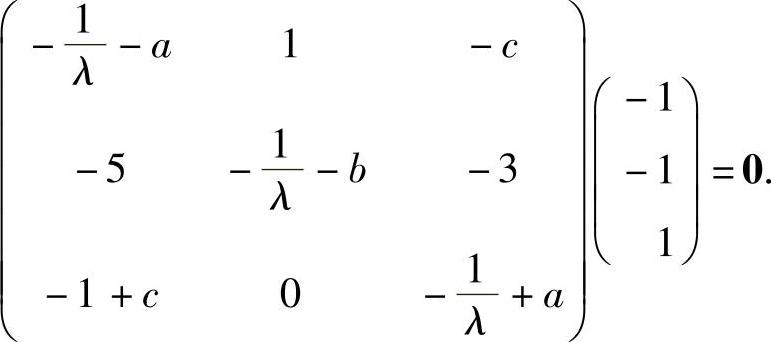
由此得到 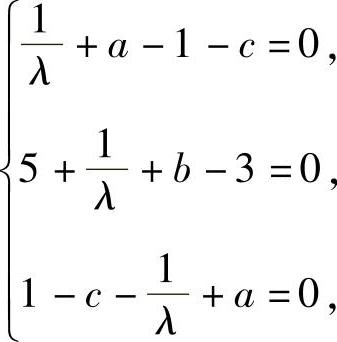
化简后得 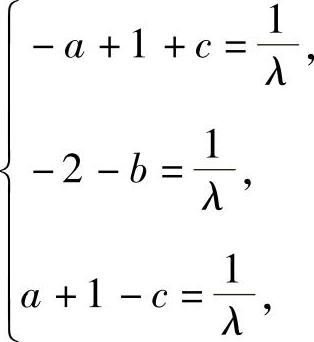 即a=c,b=-3,λ=1.
即a=c,b=-3,λ=1.
再由A=-1,即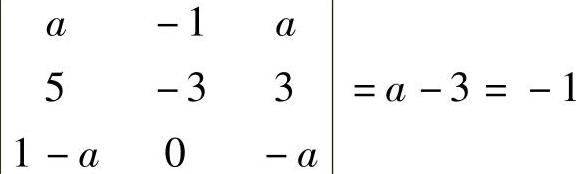 ,得a=c=2.因此所求的a=2,b=-3,c=2,λ=1.
,得a=c=2.因此所求的a=2,b=-3,c=2,λ=1.
例11.5 设A是三阶实对称矩阵.
(1)当秩r(A)=2,且A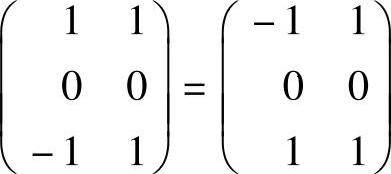 时,求A的所有特征值与特征向量;
时,求A的所有特征值与特征向量;
(2)当A的各行元素之和均为3,且向量α1=(-1,2,-1)T,α2=(0,-1,1)T是线性方程组Ax=0的两个解时,求A的所有特征值与特征向量.
精解 (1)由题设得
所以A有特征值λ=-1,1,它们对应的所有特征向量分别为
C1(-α1)=C1(1,0,-1)T,C2α2=C2(1,0,1)T,
其中,C1,C2都是任意非零常数.
由于r(A)=2,即A=0,所以A还有一个特征值为0,设它对应的特征向量为α3=(x1,x2,x3)T,则由A是实对称矩阵知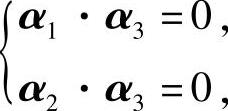 即
即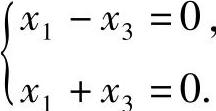
由此得到α3=C3(0,1,0)T(C3是任意非零常数).
(2)由A的各行元素之和均为3知,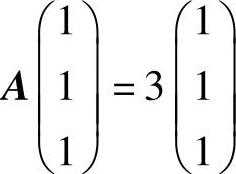 ,即A有特征值λ=3,其对应的特征
,即A有特征值λ=3,其对应的特征
向量为ξ1=C1(1,1,1)T(C1是任意非零常数).
由α1,α2是Ax=0的两个解,知
Aα1=0·α1, Aα2=0·α2,
即A有特征值λ=0(二重,这是因为α1,α2线性无关),且其对应的特征向量为
ξ2=C2α1+C3α2=(-C2,2C2-C3,-C2+C3) (其中C2,C3是任意不全为零的常数).
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







