设二阶常系数线性微分方程

y″+py′+qy=f（x） （p，q是常数，f（x）是已知函数）， （∗）它对应的齐次线性微分方程为

y″+py′+qy=0. （∗∗）

式（∗∗）的通解Y可按它的特征方程r²+pr+q=0计算.

当f（x）是P_l（x）e^αx，或e^αx[P_m（x）cosβx+Q_n（x）sinβx]（其中P_l（x），P_m（x），Q_n（x）分别是l，m，n次多项式），或它们的线性组合时，则可按有关公式算出式（∗）的一个特解y∗.此时式（∗）的通解为

y=Y+y^∗.

例8.1 求微分方程y″+a²y=sin x的通解，其中a＞0.

精解 所给的常系数线性微分方程对应的齐次线性微分方程的特征方程为

r²+a²=0， （1）故有特征根r=-ia，ia.从而齐次线性微分方程的通解为

Y=C₁ cos ax+C₂ sin ax.

下面计算所给微分方程的特解.由于所给微分方程的右端sin x=e^0x[0·cos（1·x）+1·sin（1·x）]，所以应分以下两种情形计算所给微分方程的特解y^∗：

当a≠1时，0+1×i=i不是特征方程（1）的根，所以

y^∗=Acos x+Bsin x.将它代入所给的微分方程得A=0，，所以此时当a=1时，0+1×i=i是特征方程（1）的根，所以

y^∗=x（A₁ cos x+B₁ sin x）.将它代入所给的微分方程得，B1=0，所以此时于是，当a≠1时，所给微分方程的通解为

当a=1时，所给微分方程的通解为

例8.2 设函数y=y（x）在（-∞，+∞）上具有二阶导数，且y′≠0，x=x（y）是y=y（x）的反函数，它满足微分方程

求满足y（0）=0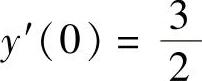，的解y=y（x）.

精解 所给微分方程不是常系数的，因此将y看做未知函数，x看做自变量，改换这个微分方程.

将它代入所给微分方程得

即(www.daowen.com)

式（1）对应的齐次线性微分方程有通解

Y=C₁e^x+C_2e^-x.此外，式（1）有特解y^∗=Acos x+Bsin x.将它代入式（1）得A=0，，所以y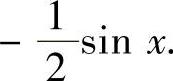^∗=因此式（1）的通解为

且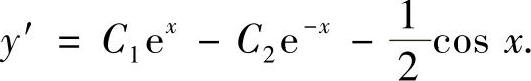于是，由y（0）=0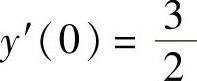，得C₁=1，C₂=-1.因此满足y（0）=0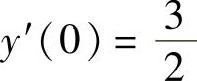，的微分方程的解为

例8.3 求微分方程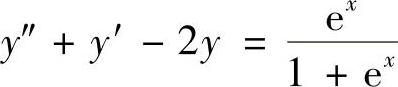的通解.

精解 所给微分方程是二阶常系数线性微分方程，但右端函数不是e^αxP_l（x）或e^αx[Q_m（x）cosβx+R_n（x）sinβx]（其中P_l（x），Q_m（x），R_n（x）分别是l、m、n次多项式）形式，所以它的特解y^∗不能用常规方法计算.因此用降阶法求解.

由于y″+y′-2y=（y″+2y′）-（y′+2y）=（y′+2y）′-（y′+2y），所以令u=y′+2y，则所给微分方程成为一阶线性微分方程

它的通解为

即y′+2y=e^x[C₁-ln（1+e^-x）].它的通解，即所给微分方程的通解为

其中，

（以上计算中的不定积分不必加任意常数）.

将式（2）代入式（1）得

例8.4 求满足下列方程的可微函数f（x）：

精解 为消去积分运算，所给方程两边对x求导得

即两边对x求导得

f′（x）=-f（-x）， （2）且f′（-x）=-f（x）.于是有f″（x）=f′（-x）=-f（x），即f″（x）+f（x）=0.（3）故f（x）满足二阶常系数齐次线性微分方程（3），它的通解为

f（x）=C₁ cos x+C₂ sin x，且f′（x）=-C₁ sin x+C₂ cos x.

将f（0）=1（由式（1）得到）和f′（0）=-1（由式（2）得到）代入以上两式得

C₁=1，C₂=-1，所以，f（x）=cos x-sin x.