【摘要】:设D是以光滑或分段光滑闭曲线C为边界的平面闭区域,函数P(x,y),Q(x,y)在D上有连续的偏导数,则其中左边的曲线积分是沿C的正向.关于坐标的平面曲线积分,往往可用格林公式作快捷计算.注 (ⅰ)如果Г不是闭曲线,则计算时,可以适当添上一曲线γ,使得Γ+γ构成闭曲线(不妨设其为正向),则可如下那样应用格林公式计算,y)dx+Q(x,y)dy:(ⅱ)当或在闭区域D的内部有不连续点(x0,y0)时,

设D是以光滑或分段光滑闭曲线C为边界的平面闭区域,函数P(x,y),Q(x,y)在D上有连续的偏导数,则
其中左边的曲线积分是沿C的正向.
注 (ⅰ)如果Г不是闭曲线,则计算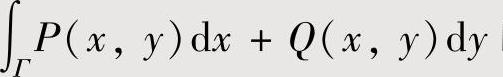 时,可以适当添上一曲线γ,使得Γ+γ构成闭曲线(不妨设其为正向),则可如下那样应用格林公式计算
时,可以适当添上一曲线γ,使得Γ+γ构成闭曲线(不妨设其为正向),则可如下那样应用格林公式计算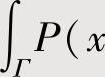 ,y)dx+Q(x,y)dy:
,y)dx+Q(x,y)dy:
(ⅱ)当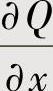 或
或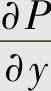 在闭区域D的内部有不连续点(x0,y0)时,则计算
在闭区域D的内部有不连续点(x0,y0)时,则计算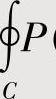 (x,y)dx+Q(x,y)dy(C是D的正向边界)时,可以作一位于D内部的、包围点(x0,y0)的闭曲线C0(方向为负向),于是
(x,y)dx+Q(x,y)dy(C是D的正向边界)时,可以作一位于D内部的、包围点(x0,y0)的闭曲线C0(方向为负向),于是
例6.1 求以下的曲线积分:
(1)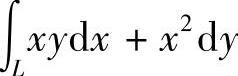 ,其中L:y=1-x(x∈[-1,1]),起点A(-1,0),终点B(1,0);(www.daowen.com)
,其中L:y=1-x(x∈[-1,1]),起点A(-1,0),终点B(1,0);(www.daowen.com)
(2)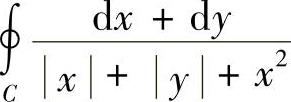 ,其中C:x+y=1(正向).
,其中C:x+y=1(正向).
精解 (1)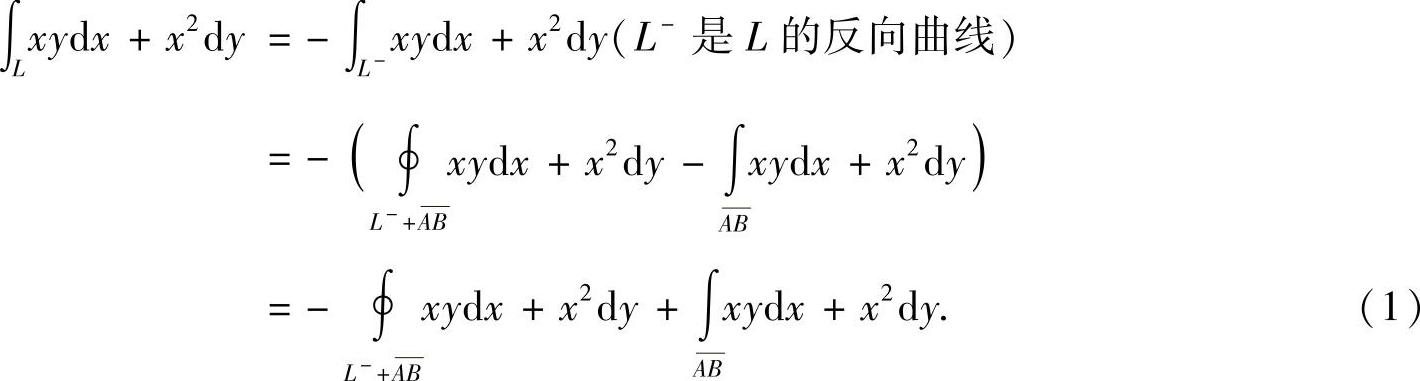 其中,
其中,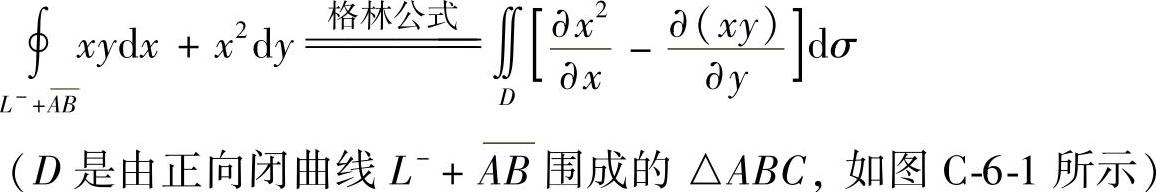
 将它们代入式(1)得
将它们代入式(1)得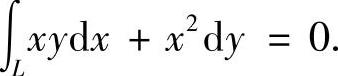
图 C-6-1
(2)由于被积函数中的(x,y)∈C,即满足x+y=1,所以有
例6.2 计算曲线积分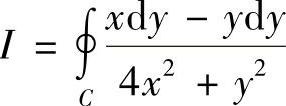 ,其中C是以点(1,0)为中心、R(R>1)为半径的正向圆周.精解 记由C围成的闭区域为D,则
,其中C是以点(1,0)为中心、R(R>1)为半径的正向圆周.精解 记由C围成的闭区域为D,则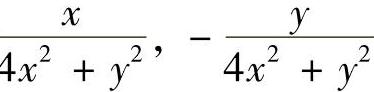 在D内有不连续点(0,0).因此作负向闭曲线Cε:4x2+y2=ε2(其中ε是充分小的正数,它使Cε位于D的内部),于是
在D内有不连续点(0,0).因此作负向闭曲线Cε:4x2+y2=ε2(其中ε是充分小的正数,它使Cε位于D的内部),于是
其中,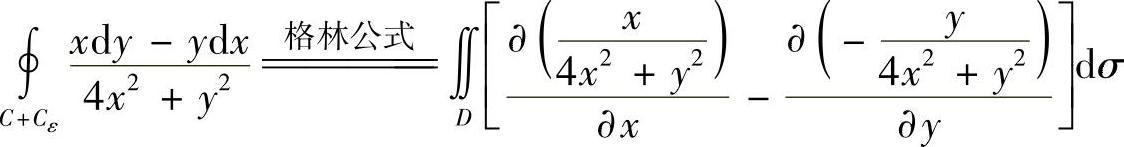
 将它们代入式(1)得 I=π.
将它们代入式(1)得 I=π.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







