当数列极限不易用运算法则和函数极限计算时,往往使用极限存在准则进行计算.
数列极限有以下两个存在准则:
数列极限存在准则Ⅰ 设数列{xn},{yn},{zn},如果它们满足yn≤xn≤zn(n=1,2,…),且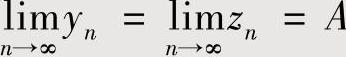 ,
,
注 在利用数列极限存在准则Ⅰ计算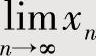 时,可以通过适当缩小与放大xn,寻找数列{yn}与{zn}.
时,可以通过适当缩小与放大xn,寻找数列{yn}与{zn}.
数列极限存在准则Ⅱ 设数列{xn}单调不减有上界或单调不增有下界,则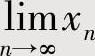 存在.
存在.
注 当{xn}由递推式x1,xn+1=f(xn)(n=1,2,…)定义时,往往使用这一准则,并且当证得 n存在时,记其极限为A,对所给递推式两边令n→∞取极限得A=f(A).解此方程所得A的值,即为
n存在时,记其极限为A,对所给递推式两边令n→∞取极限得A=f(A).解此方程所得A的值,即为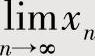 的值.
的值.
例2.1 计算下列数列极限:
(1)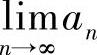 ,其中
,其中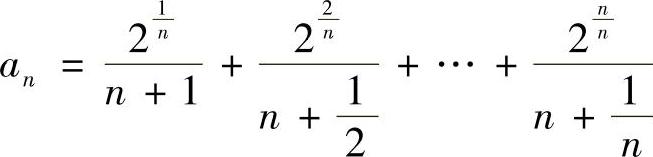 ,n=1,2,…;
,n=1,2,…;
(2) ,其中
,其中 ,2,….
,2,….
精解 (1)由于 不是某个函数的积分和式,现对它作适当缩小与放大得
不是某个函数的积分和式,现对它作适当缩小与放大得
并且 所以由数列极限存在准则Ⅰ知
所以由数列极限存在准则Ⅰ知
(2)容易看到
并且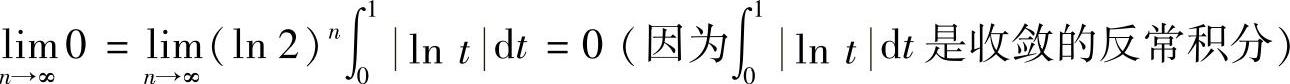 ,所以,由数列极限存在准则Ⅰ知
,所以,由数列极限存在准则Ⅰ知
例2.2 证明:
(1)1-2t2<cos 2t<1(0<t≤1);
精解 (1)对t∈(0,1],显然有cos 2t<1,下面证1-2t2<cos 2t.
记f(t)=cos 2t-(1-2t2),则它在[0,1]上连续,在(0,1)内可导且
f′(t)=-2sin 2t+4t=2(2t-sin 2t)>0,所以,对于t∈(0,1]有f(t)>f(0)=0,即1-2t2<cos 2t.(https://www.daowen.com)
(2)由(1)中已证的不等式知
其中 所以,由数列极限存在准则Ⅰ得
所以,由数列极限存在准则Ⅰ得
例2.3 求下列极限:
(1)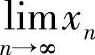 ,其中{xn}是由递推式0<x1<π,xn+1=sin xn(n=1,2,…)定义的数列;
,其中{xn}是由递推式0<x1<π,xn+1=sin xn(n=1,2,…)定义的数列;
(2)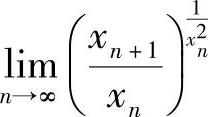 ,其中{xn}是(1)中定义的数列.
,其中{xn}是(1)中定义的数列.
精解 (1)由于{xn}是由递推式定义的,所以宜用数列极限存在准则Ⅱ求解.由x1∈(0,π)知{xn}是正项数列(容易看到xn<1,n=2,3,…),
xn+1=sin xn<xn (n=1,2,…),即{xn}单调减少有下界,所以由数列极限存在准则Ⅱ知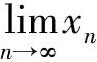 存在,记为A,则A∈[0,1).
存在,记为A,则A∈[0,1).
在递推式xn+1=sin xn的两边令n→∞取极限得A=sin A.显然在[0,1)上该方程仅有解A=0.因此
(2)由于 ,所以将上式右边的xn换为x,得1∞型未定式极限
,所以将上式右边的xn换为x,得1∞型未定式极限
其中, 因此
因此 从而
从而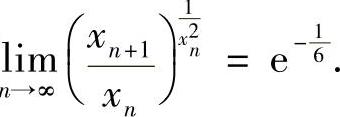
例2.4 (1)证明:对任意的正整数n,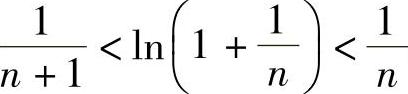 成立;
成立;
(2)设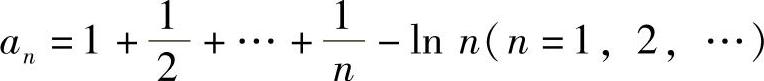 ,证明数列{an}收敛.
,证明数列{an}收敛.
精解 (1)ln(1+x)在 上满足拉格朗日中值定理条件,所以存在ξ∈
上满足拉格朗日中值定理条件,所以存在ξ∈ ,使得
,使得
即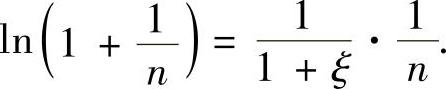 所以由
所以由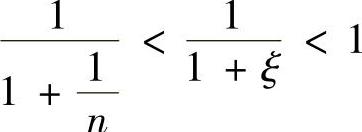 得
得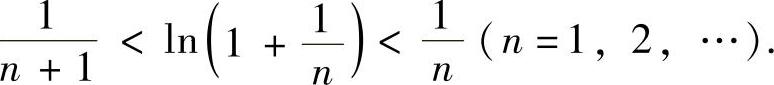
(2)现用数列极限存在准则Ⅱ证明{an}收敛.对n=1,2,…,由
以及 知{an}单调减少有下界.因此由数列极限存在准则Ⅱ知{an}收敛.
知{an}单调减少有下界.因此由数列极限存在准则Ⅱ知{an}收敛.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






