一、选择题（第1～8小题，每小题4分，共32分.下列每题给出的四个选项中，只有一个选项符合题目要求.）（1）已知极限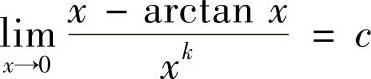，其中k，c为常数，且c≠0，则

[ ]

（2）曲面x²+cos（xy）+yz+x=0在点（0，1，-1）处的切平面方程为

（A）x-y+z=-2. （B）x+y+z=0.

（C）x-2y+z=-3. （D）x-y-z=0.

[ ]

（3）设f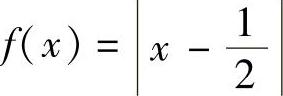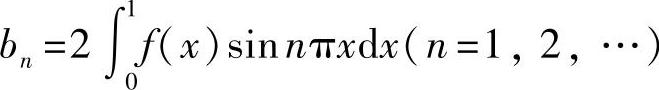，，令，

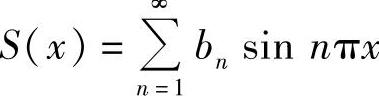则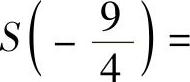

[ ]

（4）设L₁：x²+y²=1，L₂：x²+y²=2，L₃：x²+2y²=2，L₄：2x²+y²=2为四条逆时针方向的平面曲线，记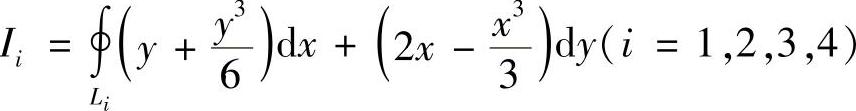，则max{I₁，I₂，I₃，I₄}=

（A）I₁. （B）I₂. （C）I₃. （D）I_4.

[ ]

（5）设A，B，C均为n阶矩阵，若AB=C，且B可逆，则

（A）矩阵C的行向量组与矩阵A的行向量组等价.

（B）矩阵C的列向量组与矩阵A的列向量组等价.

（C）矩阵C的行向量组与矩阵B的行向量组等价.

（D）矩阵C的列向量组与矩阵B的列向量组等价.

[ ]

（6）矩阵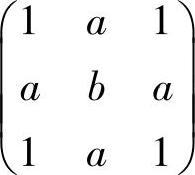与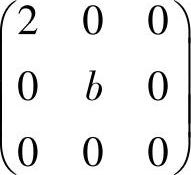相似的充分必要条件为

（A）a=0，b=2. （B）a=0，b为任意常数.

（C）a=2，b=0. （D）a=2，b为任意常数.

[ ]

（7）设X₁，X₂，X₃是随机变量，且X₁～N（0，1），X₂～N（0，2²），X₃～N（5，3²），P_i=P（-2≤X_i≤2）（i=1，2，3），则

（A）P₁＞P₂＞P₃. （B）P₂＞P₁＞P_3.

（C）P₃＞P₂＞P₁. （D）P₁＞P₃＞P_2.

[ ]

（8）设随机变量X～t（n），Y～F（1，n），给定a（0＜_a＜0.5），常数c满（X＞c）=a，则P（Y＞c²）=

（A）a. （B）1-a.

（C）2a. （D）1-2a.

[ ]

二、填空题（第9～14小题，每小题4分，共24分.）

（9）设函数y=f（x）由方程y-x=e^x（l^-y）确定，则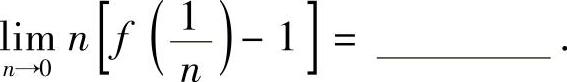

（10）已知y₁=e^3x-xe^2x，y₂=e^x-xe^2x，y₃=-xe^2x是某二阶常系数非齐次线性微分方程的3个解，则该方程的通解y=____.

（11）设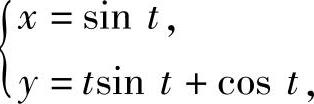（t为参数），则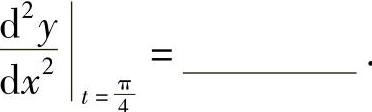

（13）设A=（a_ij）是3阶非零矩阵，|A|为A的行列式，A_ij为a_ij的代数余子式.若a_ij+A_ij=0（i，j=1，2，3），则|A|=____.(www.daowen.com)

（14）设随机变量Y服从参数为1的指数分布，a为常数且大于零，则P（Y≤a+1Y＞a）=____.

三、解答题（第15～23小题，共94分.解答应写出文字说明、证明过程或演算步骤.）

（15）（本题满分10分）

计算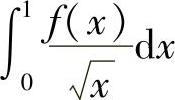，其中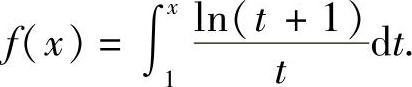

（16）（本题满分10分）

设数列{a_n}满足条件：a₀=3，a₁=1，a_n-2-n（n-1）a_n=0（n≥2）.S（x）是幂级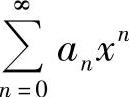数的和函数.

（Ⅰ）证明：S″（x）-S（x）=0；

（Ⅱ）求S（x）的表达式.

（17）（本题满分10分）

求函数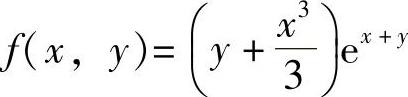的极值.

（18）（本题满分10分）

设奇函数f（x）=[-1，1]上具有二阶导数，且f（1）=1，证明：

（Ⅰ）存在ξ∈（0，1），使得f′（ξ）=1.

（Ⅱ）存在η∈（-1，1），使得f″（η）+f′（η）=1.

（19）（本题满分10分）

设直线L过A（1，0，0），B（0，1，1）两点，将L绕z轴旋转一周得到曲面Σ，Σ与平面z=0，z=2所围成的立体为Ω.

（Ⅰ）求曲面Σ的方程；

（Ⅱ）求Ω的形心坐标.

（20）（本题满分11分）

设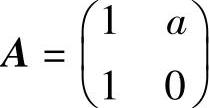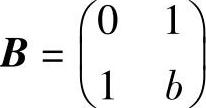，，当a，b为何值时，存在矩阵C使得AC-CA=B，并求所有矩阵C.

（21）（本题满分11分）

设二次型f（x₁，x₂，x₃）=2（a₁x₁+a₂x₂+a₃x₃）²+（b₁x₁+b₂x₂+b₃x₃）²，

记，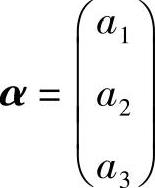

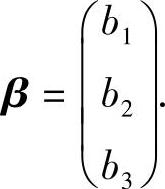
（Ⅰ）证明二次型f对应的矩阵为2αα^T+ββ^T；

（Ⅱ）若α，β正交且均为单位向量，证明f在正交变换下的标准形为2y²₁+y²_2.

（22）（本题满分11分）

设随机变量X的概率密度为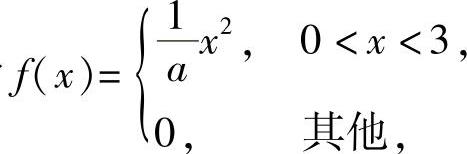令随机变量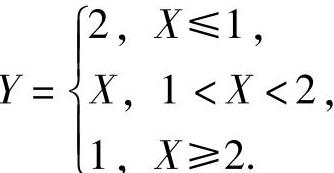

（Ⅰ）求Y的分布函数；

（Ⅱ）求概率P（X≤Y）.

（23）（本题满分11分）

设总体X的概率密度为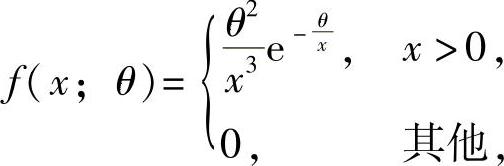其中θ为未知参数且大于零，X₁，X₂，…，X_n为来自总体X的简单随机样本.

（Ⅰ）求θ的矩估计量；

（Ⅱ）求θ的最大似然估计量.