求解域内的流动是由边界条件驱动的，从某种意义上来说，求解流动问题不过是把定义在边界轮廓上或者表面上的一组数值外推到计算域内部，因此给出物理上切合实际的边界条件极其重要，边界条件选择不当一般是造成数值计算失败的主要原因。前面我们已讨论了流体流动最实用的边界条件，包括入口条件、出口条件和壁面条件以及怎样使它们应用到有限容积法之中。之后我们提出了三个更进一步的条件：定压条件、对称条件和周期性边界条件。它们在实际的计算中是很有用的，在物理上也是切合实际的，当然，边界条件还不仅仅是这些。

若我们试图在一个有壁面边界和一个流动入口而没有出口边界的计算域中寻求定常状态的解，显而易见，在定常状态下质量不能守恒，且数值计算迅速“膨胀”。这个例子也暗示一定类型的边界条件必须同时伴有其他特殊的边界条件。现在我们简要列举一些允许的组合：

1）只有壁面

2）壁面和入口，至少有一个出口

3）壁面和入口，至少有一个定压边界

4）壁面和定压边界

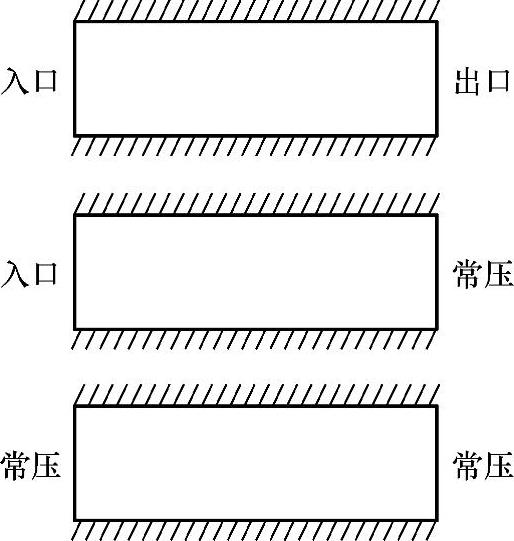
图4.13.17 简单管道流动边界条件

图4.13.17为简单管道流动中的情况。使用出口边界条件时要特别注意，出口边界条件只能用于这样的情况：若所有流入计算域内的流动是根据入口边界条件，即在入口设定的速度和数性变量给出时，推荐使用的流动区域只有一个出口。从物理上来看，出口压力控制着多个出口间的分流，因此，定义在出口的量值要比用零梯度出口条件好。不允许把一个出口条件与一个或多个定压边界一起使用，因零梯度出口条件既不规定出口的流率也不规定出口的压力，将使问题不确定。(www.daowen.com)

对于出口边界位置的确定，也应进行合适的选择。如果出口边界离固体障碍物很近的话，流动有可能无法达到充分发展的状态，这可能会导致相当大的误差。图4.13.18表示出了障碍物下游典型的速度剖面，说明在出口边界位置选择上可能会出现问题。如果出口位于接近障碍物的地方，它可能会横过一个带回流的尾流区。这时不仅假定的梯度条件不满足，而且还存在一个反向流动区。虽然我们已经假设流动是向外的，但反向流动区的流体会流向控制域内，若发生了这样的情况，我们就不能信赖得出的解。再往下游一点，就可能不存在反向流动，但速度剖面在流动方向上仍在变化，所以零梯度条件还不满足。根据经验经常把出口边界放在最后一个障碍物的十倍于高度远的下游，这样有望得到准确的解。为了获得高精度的解，有必要通过对不同下游距离影响的敏感性研究，证实出口位置的选择已对内部解没有影响。

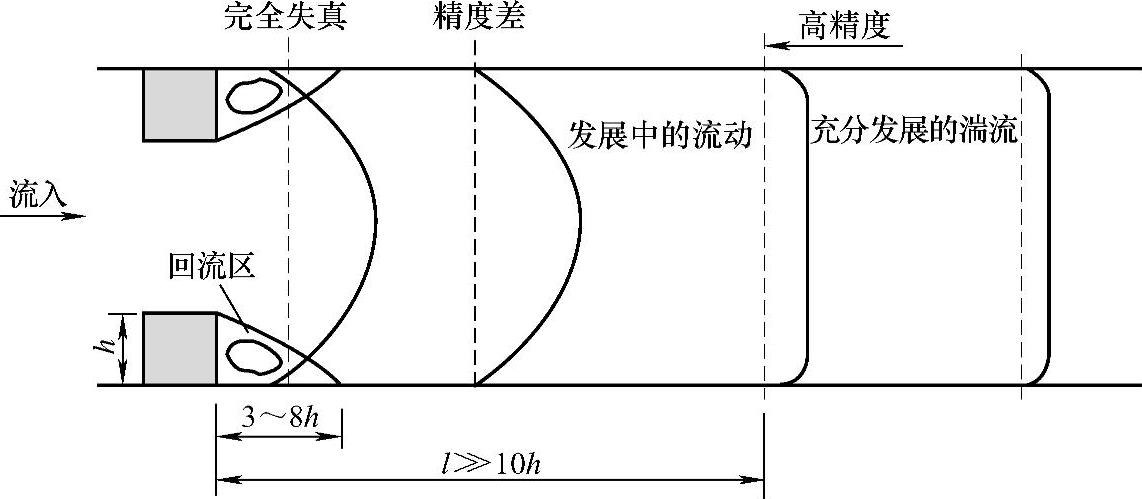
图4.13.18 障碍物下游不同位置速度分布

关于近壁面网格附近的边界处理，对于湍流流动，最准确的方法就是使用壁面函数法提供的经验拟合。采用在层流线性底层内也布置结点来进行模拟的方法，为了得到同样的精度，网格必须非常细密，这是很不经济的。y⁺必须大于11.63的准则，对壁面到最近网格点的距离Δy_P规定了一个下限。我们改善精度的主要方法就是细化网格，但在湍流流动模拟过程中，我们必须确保当网格细化时，y⁺的值大于11.63，若能保证在300～500的范围内则会更好。

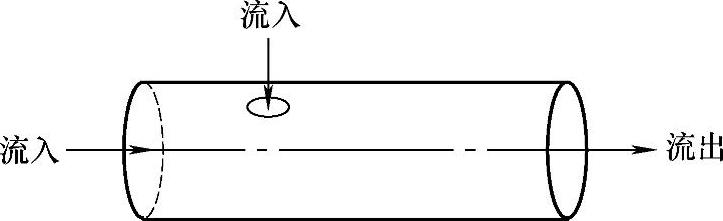
图4.13.19 非对称流动

关于对称边界条件，我们应认识到流动控制区域是几何对称的，并不总是保证流动也是对称的，这一点很重要。如图4.13.19所示，对于有侧面射流的圆管流动，尽管控制区域是轴对称的，但是横向流动的射流使流动成为非轴对称的。