固定壁面边界条件(简称固壁边界条件)是流动和传热计算中最常见的边界条件,但因涉及流动状态问题,处理起来相对比较复杂。为简单起见,我们讨论固壁边界与x坐标方向平行的情况。此时近壁处速度u平行于壁面,v垂直于壁面,图4.13.10~图4.13.12表示了近壁处网格和控制容积的细节。
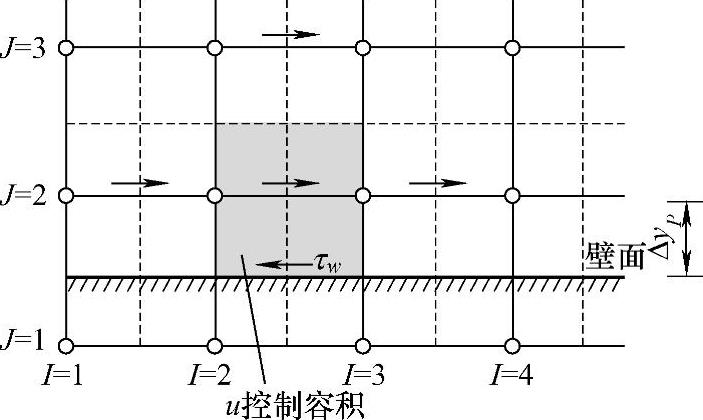
图4.13.10 固定边界u控制容积
无滑移条件是固壁处的速度边界条件,即在壁面上u=v=0。设图4.13.11a中j=2或图4.13.11b中j=NJ处垂直于壁面的速度分量v=0,则紧邻控制容积j=3(或j=NJ-1)的动量方程可不作修正。同时,因为壁面速度为已知,此处的压力修正也是不必要的,设置aS=0(或aN=0)vS∗=vS和(或vN∗=vN)即可求解紧邻壁面的控制容积的压力修正方程。
其他场变量的求解取决于近壁处流体的流动状态是层流还是湍流。若整个流场的流动状态是层流,则按层流计算;对于湍流,因流体在近壁处存在层流底层,若近壁处的网格足够密,则贴近壁面的网格内的流体流动处于层流状态。判断湍流近壁处的流态要用到无量纲距离y+。y+的计算公式为式中,ΔyP为靠近壁面的第一个结点到壁面的垂直距离,如图4.13.13所示;ν为流体的运动粘度,ρ为流体密度;τw为壁面粘性应力。
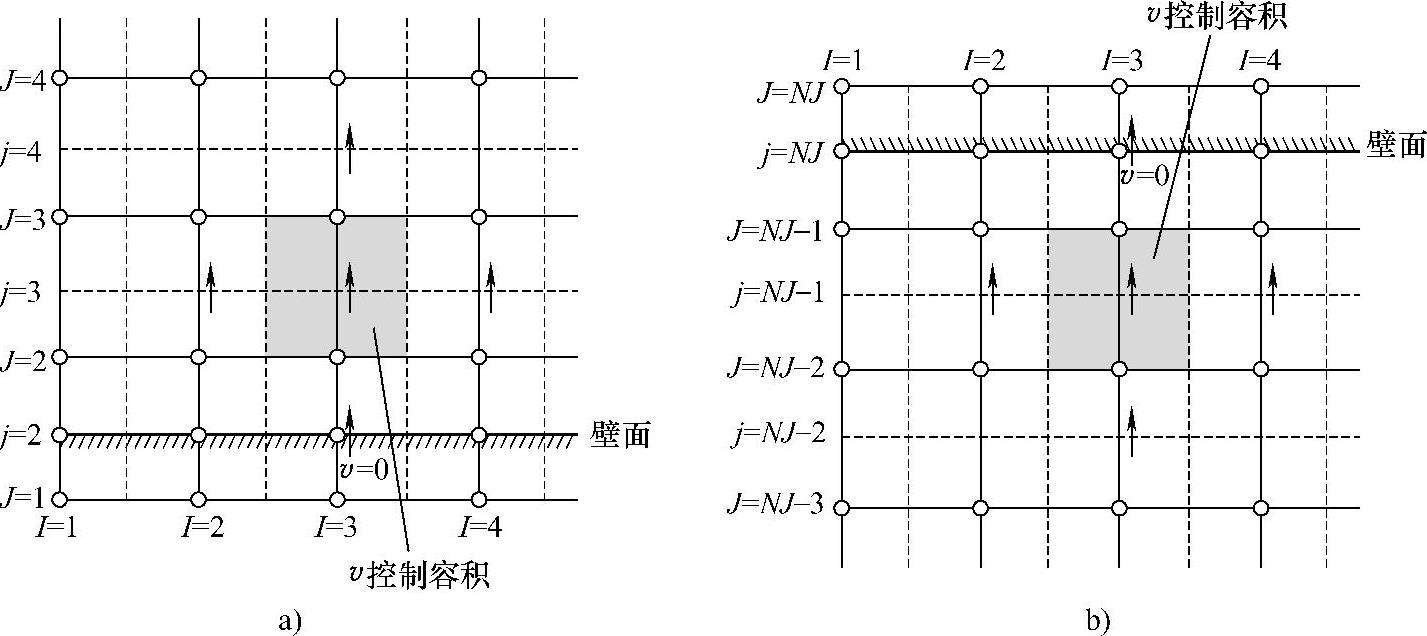
图4.13.11 入口边界v控制容积

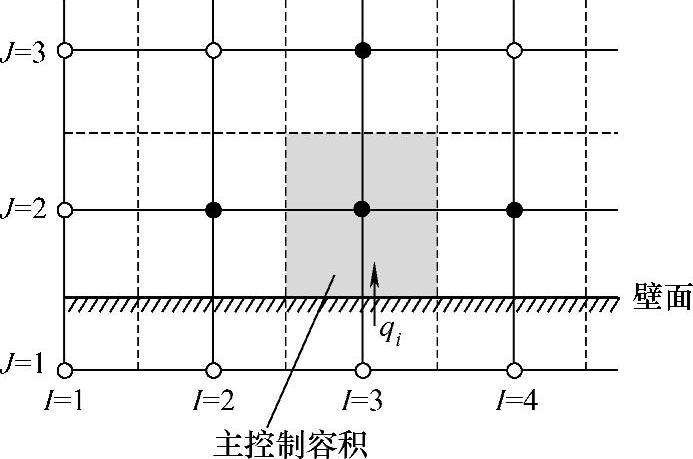
图4.13.12 固定边界主控制容积
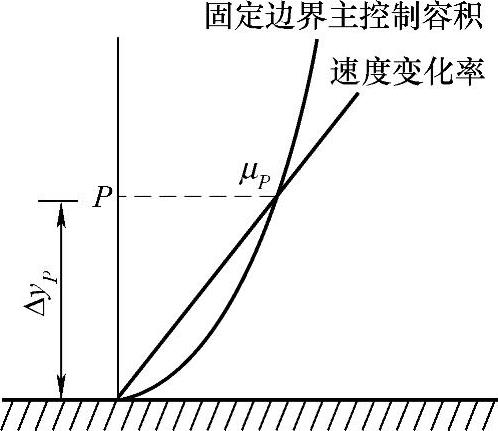
图4.13.13 近壁处速度分布
当y+≤11.63时认为流动状态与层流一样,当y+>11.63时认为流动状态为湍流。层流状态流动近壁处速度从0变化到主流速度时呈线性变化,湍流时速度变化符合对数率。11.63即为两种变化率的交点,y+通过求解方程

得到。
式中,κ为冯·卡门常数(取κ=0.4187);E为与壁面粗糙度有关的积分常数,光滑壁面且壁面剪应力为常数时,E=9.793。
可见,对主流为湍流的固壁边界条件进行处理时,首先要计算y+的值,对不同的流态要不同处理,下面不加证明地给出层流和湍流时的处理方法。
1.层流状态固壁边界条件处理
事实上这里包含两种情况,即层流流动以及y+≤11.63的湍流流动,这两种情况的固壁边界条件处理方式是一样的。
(1)u动量方程处理
层流状态壁面剪应力由下式计算

式中,uP为靠近壁面的结点处流速。
点P控制容积壁面边的剪力FS可根据剪应力计算得出,如图4.13.10所示,有
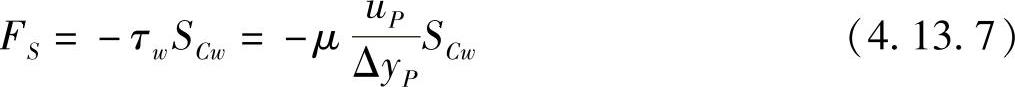
式中,SCw为控制容积位于壁面侧的面积。因此,动量方程要加入源项

(2)能量方程处理
当固体壁面温度Tw为已知时,由壁面进入控制容积的热流量为
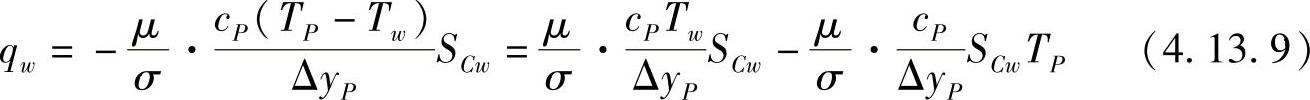
式中,cP为流体比热容;TP为P点温度;σ为层流普朗特(Prandtl)数。能量方程需要加入源项
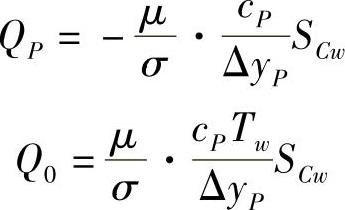
当固体壁面处有固定热流qw时,直接通过线性化处理,即
qw=Q0+QPTP
若为绝热状态时,则
Q0=QP=0
2.湍流状态固壁边界条件处理
当y+>11.63时,近壁处第一个结点P被认为是在对数率的速度变化区中,此时由于壁面到点P的距离太大,无法真实反映它们之间的流动规律,因此,通常采用壁面函数来近似模拟壁面到点P间的情况。此外,湍流状态的流体计算,工程上多采用时均方程加湍流模型计算法。常用的湍流模型为kε两方程湍流模型,因此计算方程组中除动量方程和连续性方程外,还需额外求解两个方程——湍流动能k方程和湍动耗散率ε方程。壁面函数的公式推导比较复杂,这里只给出壁面函数应用的一些结论。(https://www.daowen.com)
采用kε两方程湍流模型和壁面函数时近壁处参数间关系如下。
1)与壁面相切的动量方程
壁面剪应力
τw=ρCμ1/4kP1/2uP/u+ (4.13.10)
壁面剪力
FS=-τwSCw=-(ρCμ1/4kP1/2uP/u+)SCw (4.13.11)
2)垂直于壁面的动量方程(速度分量为0)
3)湍流动能k方程
单位体积k方程的源项=(τwuP-ρCμ3/4k3P/2u+)ΔV/ΔyP (4.13.12)
4)湍动耗散率ε方程
设置点P处的值
εP=Cμ3/4k3P/2/(κΔyP) (4.13.13)
5)能量方程
壁面热流
qw=-ρCPCμ1/4kP1/2(TP-Tw)/T+ (4.13.14)
其中,u+为无量纲速度,T+为无量纲温度,分别定义为
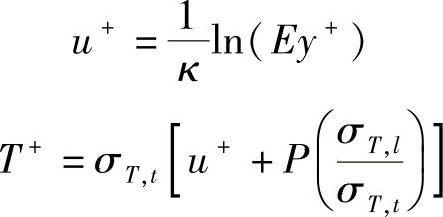
式中,σT,l为层流普朗特数,σT,t为湍流普朗特数σT,t≈0.9,σT,l和σT,t之间的关系为
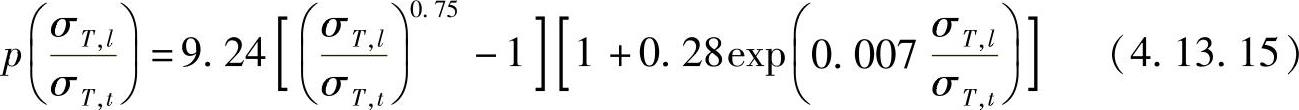
由式(4.13.15)可解出σT,l/σT,t,从而可求出T+和u+。有了这些关系式,就可对壁面处控制容积的离散方程进行修正,用壁面函数模拟近壁处湍流状态。
(1)平行于壁面的u速度动量方程
方程与控制容积南侧面(壁面)的联系切断,即aS=0。壁面剪力FS的计算公式为式(4.13.11),u动量方程的源项为
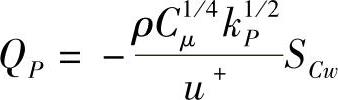
(2)湍流动能k方程
首先置aS=0,式(4.13.12)表示的单位体积源项的第一项中有k3/2,将其线性化为(kP∗)1/2kP,其中,kP∗作为前次迭代或初始设置的已知k值,于是k方程的源项为
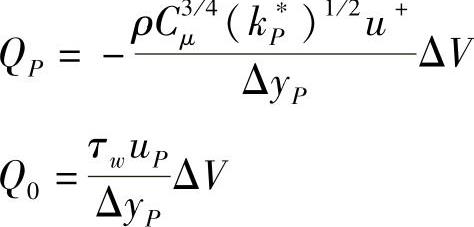
(3)湍动耗散率ε方程
按式(4.13.13)给出近壁结点P处ε的固定值εP。因此设置ε方程的源项为
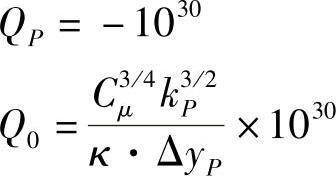
(4)温度方程
首先置aS=0,壁面温度Tw为一定值时,壁面热流由式(4.13.15)计算,设置温度方程的源项为
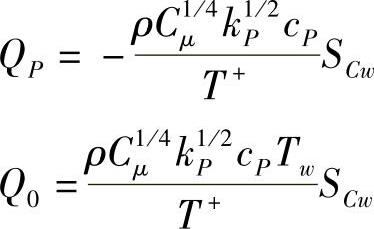
若壁面热流qw为一定值,设
qw=Q0+QPTP
若边界绝热,则
Q0=QP=0
应当指出,壁面函数的应用是有一定条件的,必须满足高雷诺数流动条件,而且流体流动速度平行于壁面,速度的变化只能发生在垂直于壁面的方向,流动方向上没有压力梯度。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







