【摘要】:采用交错网格系统时u动量方程采用一种网格,v动量方程采用另一种网格,其余场变量采用主控制容积网格,边界条件处理时也会在不同的网格中涉及不同的结点。入口处要指定流动变量在入口边界结点处的值。图4.13.2~图4.13.5表示了边界处计算第一个内点的起始控制容积位置和相关点的位置。入口边界值uin,vin和pi′n(=0)给定位置在I=1处,从紧邻入口边界的下游开始求解离散方程,起始控制容积在图中用阴影表示。
以二维压力与速度耦合问题求解作为边界条件讨论的基础,我们要求解的方程至少有三个,即x方向和y方向的动量方程以及压力修正方程,若还有其他场变量需求解(如温度或浓度),还要补充它们的方程。采用交错网格系统时u动量方程采用一种网格,v动量方程采用另一种网格,其余场变量采用主控制容积网格,边界条件处理时也会在不同的网格中涉及不同的结点。
入口处要指定流动变量在入口边界结点处的值。这里为简单起见,讨论入口边界与x坐标方向垂直的情况。图4.13.2~图4.13.5表示了边界处计算第一个内点的起始控制容积位置和相关点的位置。入口边界值uin,vin和pi′n(=0)给定位置在I=1(或i=2)处,从紧邻入口边界的下游开始求解离散方程,起始控制容积在图中用阴影表示。图中用箭头表明求解动量方程时的邻近速度分量u或v位置,用实心圆点表示求解压力修正方程和其他场变量离散方程时邻近相关p′或ϕ的位置。求解u,v和ϕ方程时,uin,vin和ϕin即为入口边界值,直接代入方程(或采用置大数法);对于压力修正方程,将pi′n=0代入方程即可。因入口边界处压力不用修正,所以压力修正方程的aW=0。此外,在作速度修正时入口边界速度为已知,计算式(4.9.24)的源项也不用修正,即uw∗=uW。
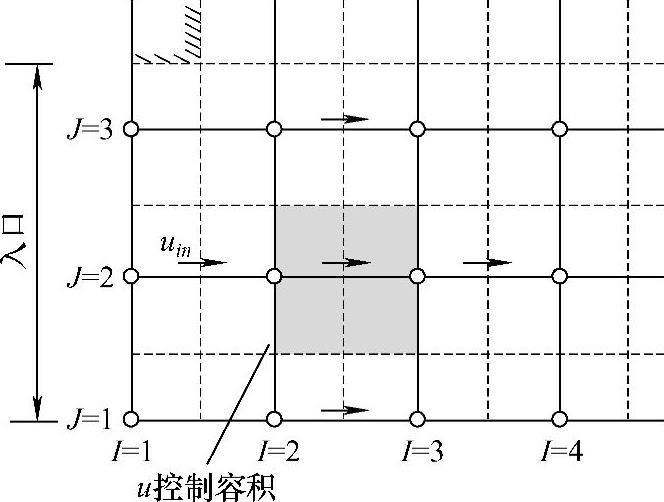
图4.13.2 入口边界u控制容积
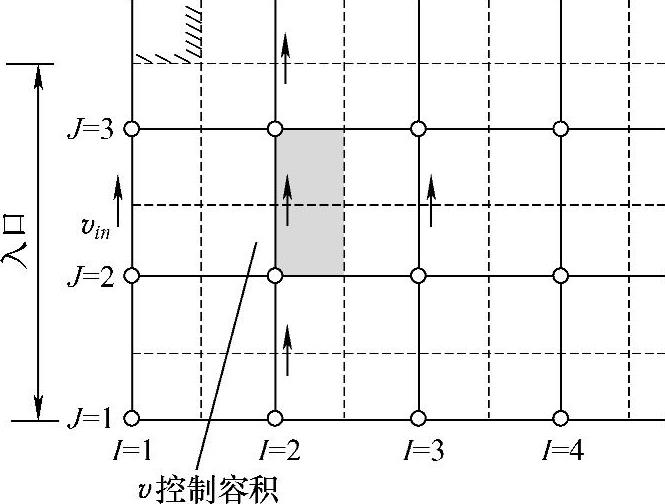
图4.13.3 入口边界v控制容积(https://www.daowen.com)
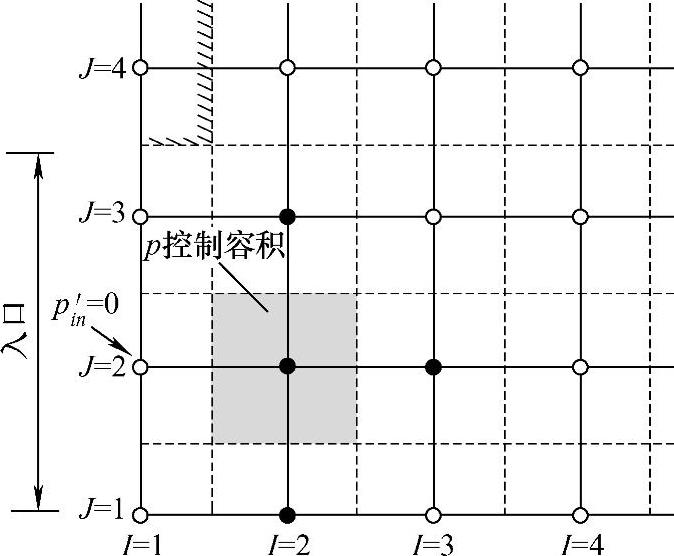
图4.13.4 入口边界p′控制容积
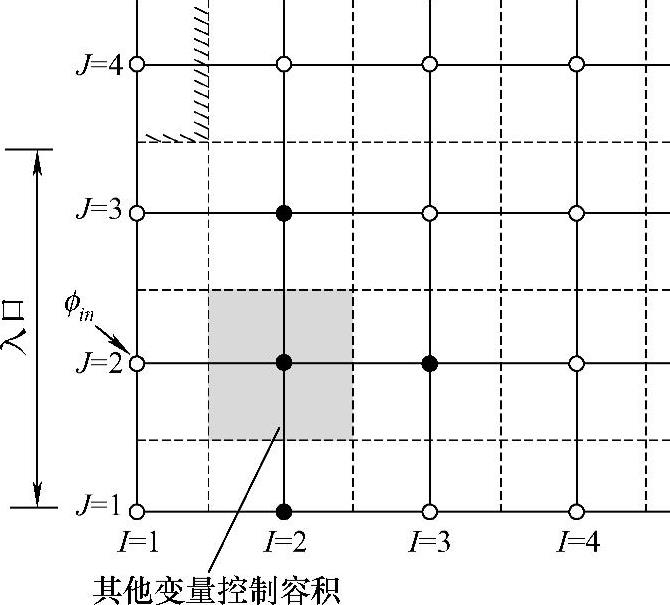
图4.13.5 入口边界主控制容积
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章






