有限体积法主要用于流体流动和传热问题的计算，这类问题除了流动或传热现象的控制微分方程外，还由初始条件和边界条件一起构成定解问题。对非稳态问题，所有计算变量在开始计算之前应有一初始值，即所有网格结点上各变量应有一计算起点，这样才有可能依时间步长计算场变量随时间变化，这就是初始条件。对数值计算来讲，初始条件的给定并不影响计算过程的实施，给定初始值即可，一般不需“额外”处理。因此这里不讨论初始条件。而大多数边界条件则会对离散方程的形式和计算方法产生一定的影响，下面来讨论边界条件的处理过程。

一般来讲，流动和传热问题的边界条件主要有入口边界条件、出口边界条件、固体壁面边界条件、压力边界条件、对称边界条件和周期性（或循环）边界条件。

对于交错网格系统，在划分网格时一般在边界外侧设置一“层”额外的结点，如图4.13.1所示。计算是在内部结点（J=2，I=2）处，边界控制容积也是如此。最外一“层”结点只是为了给定边界值之用，即物理边界与边界控制容积的外边界重合，外层结点值用于存储给定的边界值，这样布置网格可使边界条件对离散方程和边界控制容积积分的改动最小。

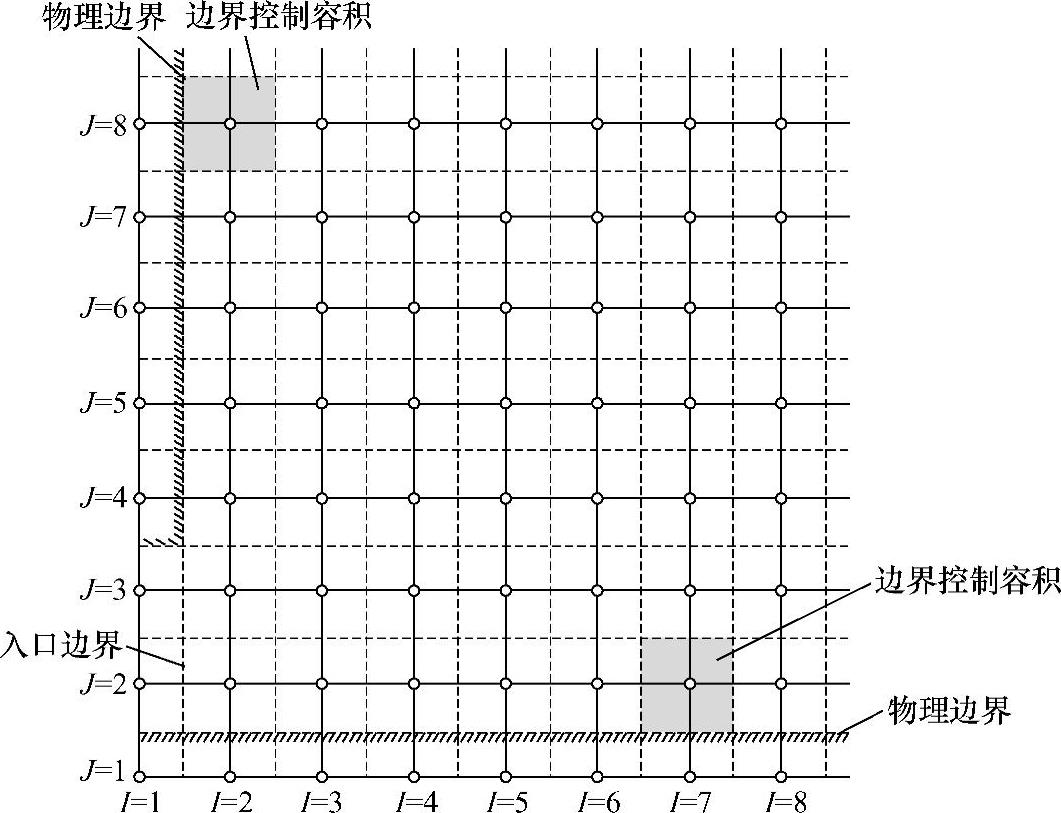
图4.13.1 边界网格设置

由本章前面讨论的算例可以看出，边界条件处理是通过切断离散方程与边界边的联系并对方程源项进行修正来实现的，即令离散方程中边界的系数为零，同时边界边的流量用精确值或线性近似值引入源项Q₀和Q_P中。当边界条件为给定流量（对流量或扩散量）时可用这种方法处理，若边界条件为给定场变量值时，可采用与第3章中“对角线项扩大法”类似的方法。例如，给定边界边场变量ϕ的值为ϕ=ϕ_fix，可采用一种称为置大数法的方法处理边界条件。令(www.daowen.com)

Q_P=-10³⁰，Q₀=10³⁰ϕ_fix （4.13.1）

将上述源项加入到离散方程中，成为

（a_P+10³⁰）ϕ_P=∑a_nbϕ_nb+10³⁰ϕfix于是

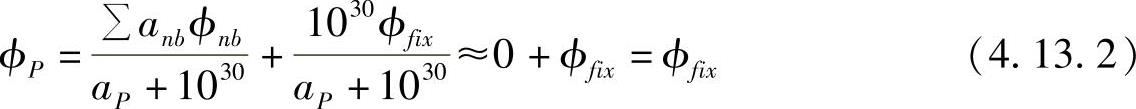
因为∑a_nbϕ_nb有界，10³⁰相对于它是一个极大数，而10³⁰/（a_P+10³⁰）≈1。这一方法不仅仅用于边界上给定结点值的计算，对于计算域内任意给定结点值的求解均可采用这种办法处理。例如，流场内有固定障碍物或固定温度热源，固体壁面处的ϕ值（u=0或T=T_w）为一定值，采用上述方法处理可不修改计算程序，不改变方程阶数，不对代数方程组产生不利影响，可在希望的结点处解出给定的值。