非稳态压力与速度耦合问题的控制微分方程在二维情况下只比相应的稳态方程多一时间相关项，即

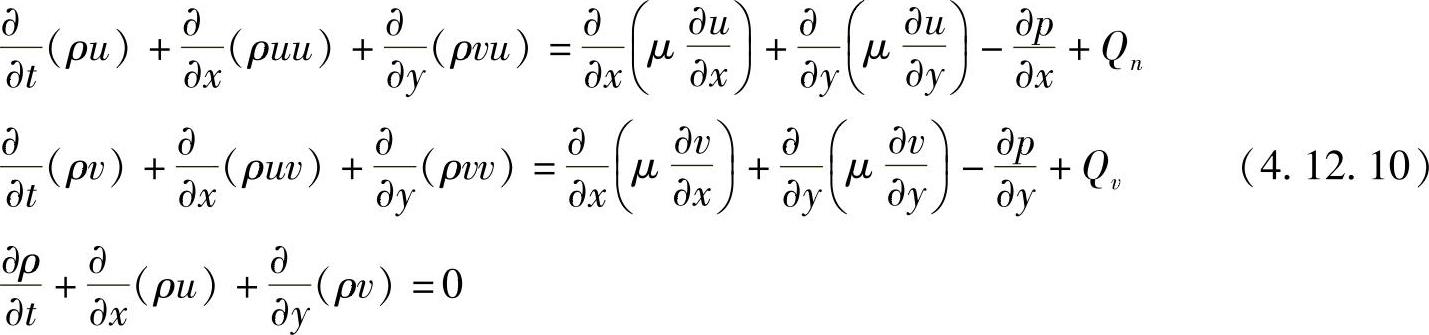
前两式为动量方程，其中与时间无关的项离散时与稳态方程离散方法相同，时间相关项的离散前文已讨论了，因此，非稳态动量方程的离散方程只比稳态情况方程式多一项a⁰_Pϕ⁰_P，且a⁰_P=ρ⁰_PΔxΔy/Δt，主控制容积结点系数为

a_P=a_W+a_E+a_S+a_N+a⁰_P-Q_P

将连续性方程在控制容积中积分，得

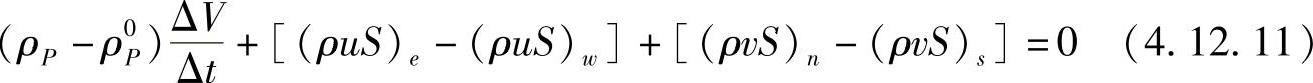
SIMPLE算法中压力修正方程是由连续性方程推导出来的，本质上仍为连续性方程。完全类似于稳态情况下压力修正方程的推导，可得非稳态问题的压力修正方程，即

a_I，Jp_I′_，J=a_I+1，Jp_I′_+1，J+a_I-1，Jp_I′_-1，J+a_I，J+1p_I′_，J+1+a_I，J-1p_I′_，J-1+b_I′_，J （4.12.12）(www.daowen.com)

式中，

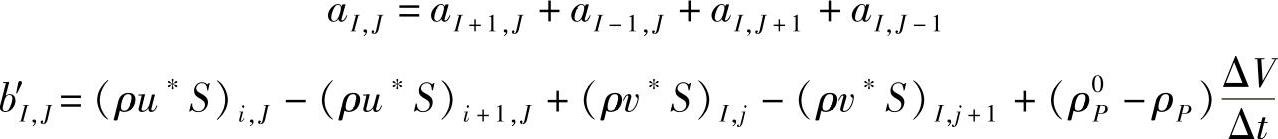
而a_I-1，J=（ρdS）_i，J，a_I+1，J=（ρdS）_i+1，J，a_I，J-1=（ρdS）_I，j，a_I，J+1=（ρdS）_I，j+1。

可见，非稳态情况压力修正方程式（4.12.12）只是源项b_I′_，J与稳态情况压力修正方程式（4.9.24）不同，b_I，′_J多了一项与时间相关的密度变化项，其余各项完全相同。因此非稳态压力与速度耦合问题的计算过程与稳态情况类似，只是多了一层时间迭代。而时间的推进格式通常可采用全隐格式。中间压力修正过程和速度修正过程则可采用SIMPLE、SIMPLER或SIMPLEC等算法中的任意一种。当每一时间层的计算结果迭代收敛之后，即可进入下一时间层的迭代计算，图4.12.1表示了瞬态SIMPLE算法的计算流程。

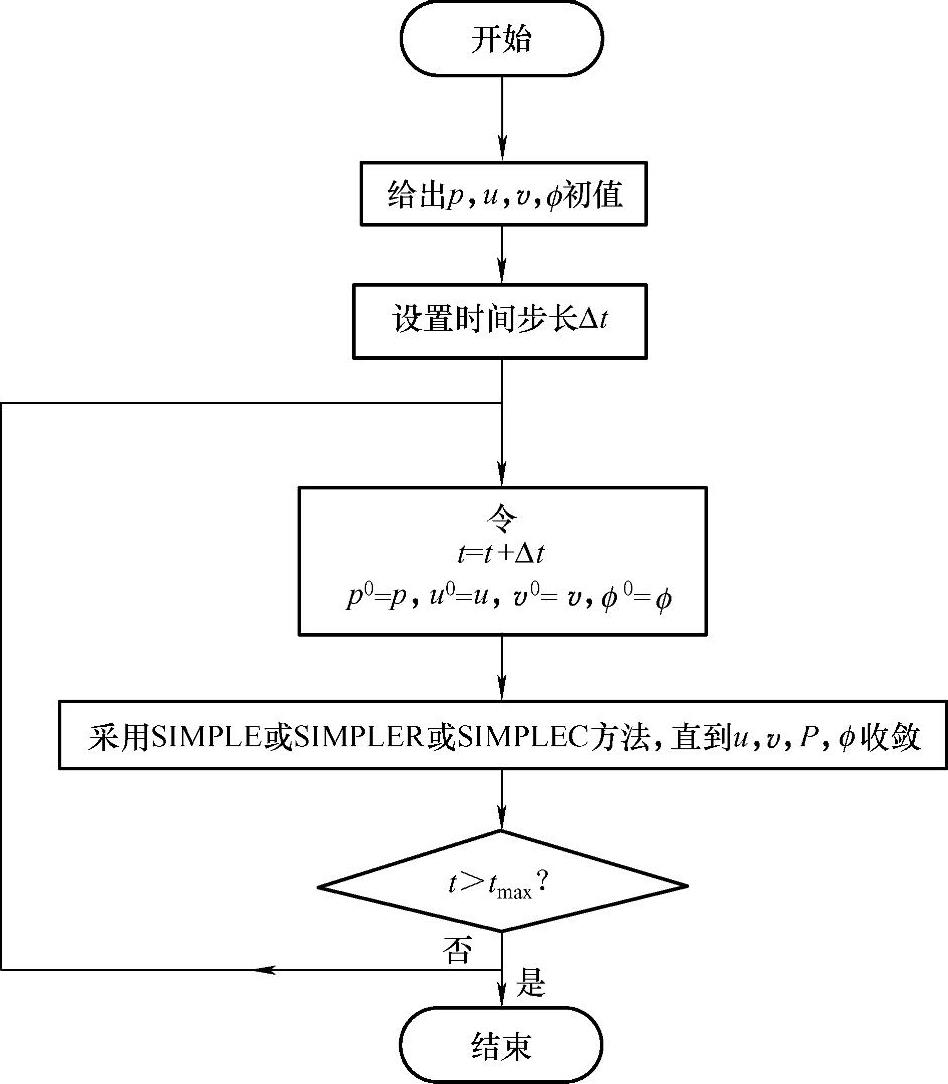
图4.12.1 非稳态问题SIMPLE算法的计算流程