1.一维非稳态热传导问题的计算格式
一维非稳态热传导问题的控制微分方程为
式中，ρ为热传导材料的密度；c为材料比热容；λ为材料导热系数。
考虑图4.5.1所示一维控制容积，在时间t到t+Δt间隔内，在控制容积内对方程式（4.11.4）积分
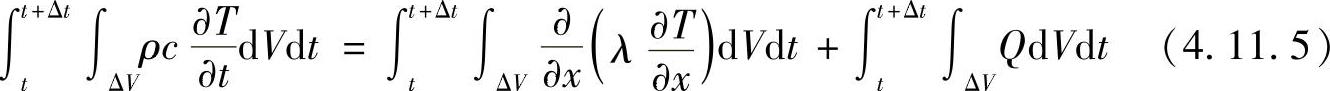
由高斯公式，式（4.11.5）可写成
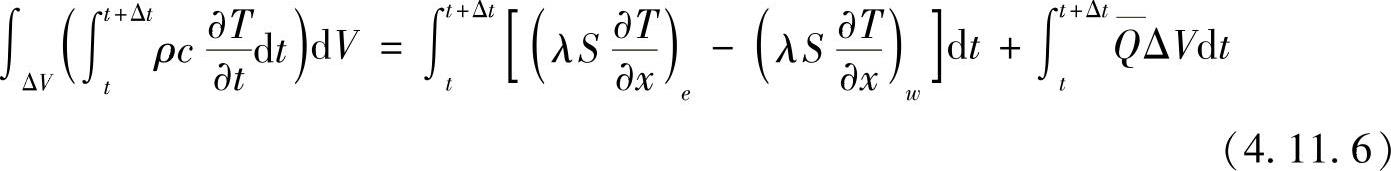
式中，S为控制容积表面积；ΔV为其体积，ΔV=SΔx，而Δx为控制容积长度δxwe；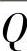
为平均源项强度。如果将
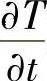取近似值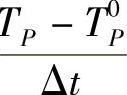
，其中，T0P为t时刻点P的温度值，TP为t+Δt时刻点P的温度值。则式（4.11.6）左端积分可写为
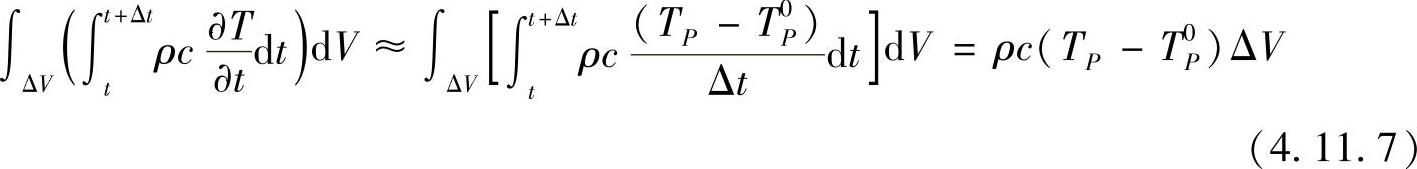
事实上，这里温度对时间的偏导数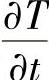
的近似相当于一阶向后差分，也可考虑采用高阶差分近似。对于式（4.11.6）右端扩散项界面值的计算，若采用中心差分，结合式（4.11.7）的结果，有
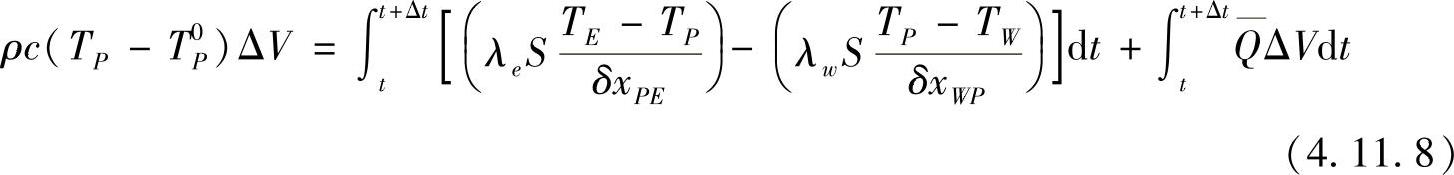
为计算式（4.11.8）右端扩散项的时间积分，需给出结点温度TP，TE，TW随时间的变化关系，而这一变化关系是不知道的。通常的处理方法是利用t时刻的温度，如T0P等，以及t+Δt时刻的温度，如TP等，由它们加权组合构成该时间间隔内的平均温度，然后积分计算，即
式中，θ=0～1，从而关于TP的时间积分IT可写为
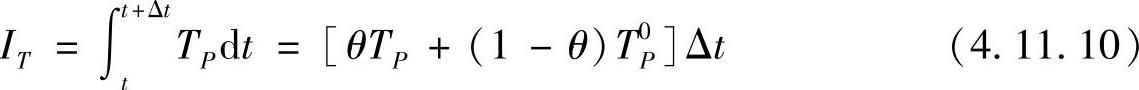
当θ=0时，意味着用t时刻的温度T0P作为平均温度；当θ=1时，意味着用t+Δt时刻的温度TP作为平均温度，当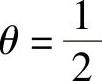
时，意味着t时刻和t+Δt时刻的温度有相当的权重，在以上三种情况下，即
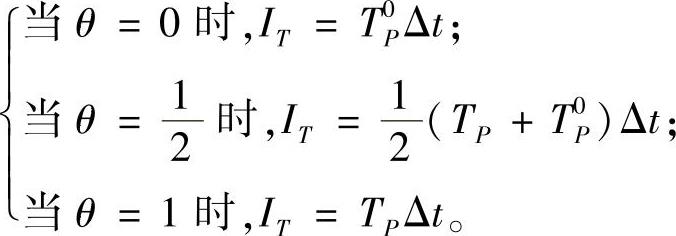
同理，可计算关于TE和TW的时间积分。利用上述积分结果，代入式（4.11.8）并将全式除以SΔt，可得
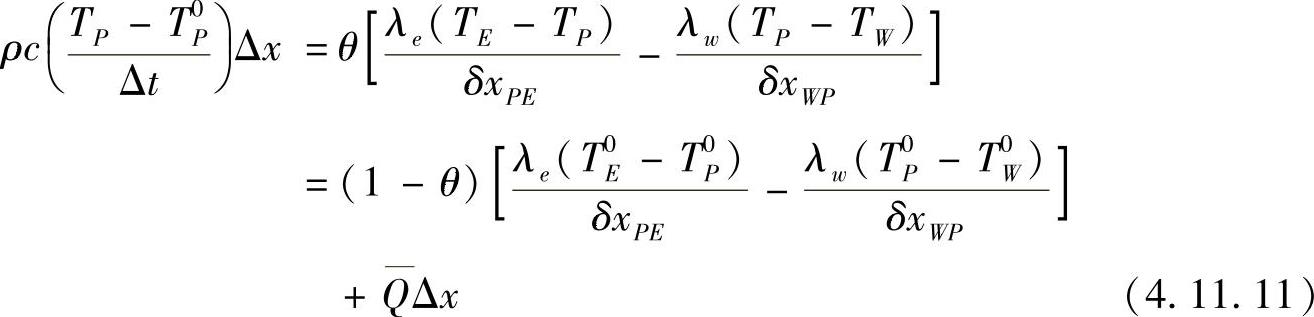
按结点温度值排列整理，有
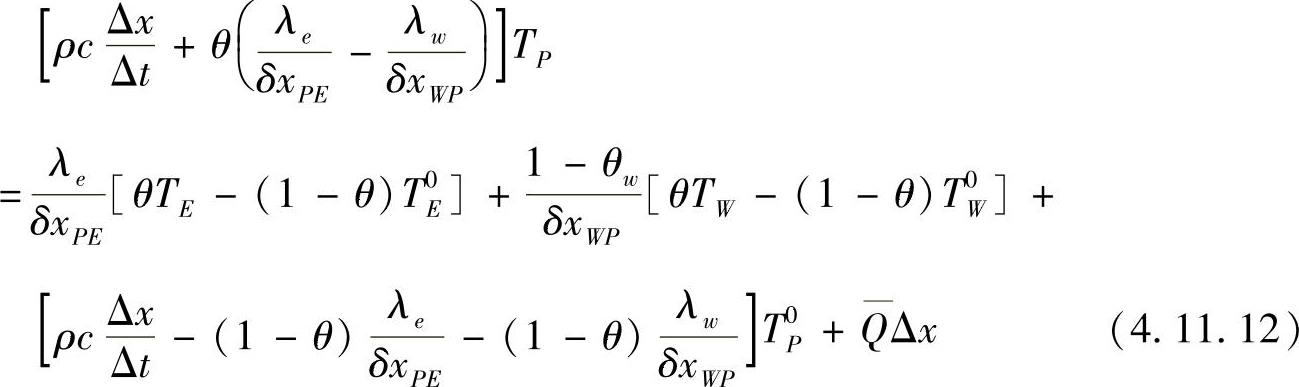
将TP，TE，TW的系数归一化处理，可得
aPTP=aW[θTW+（1-θ）T0W]+aE[θTE+（1-θ）T0E]+[a0P-（1-θ）aW-（1-θ）aE]T0P+b（4.11.13）
式中，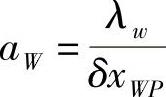
；
；
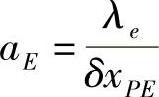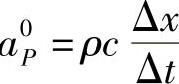；aP=θ（aW+aE）+a0P；b=QΔx
离散方程的具体形式取决于权因子θ的值。当θ=0时，只有方程式（4.11.13）右端旧时刻t的结点温度值T0P，T0E，T0W被用来计算新时刻t+Δt的结点温度值TP，这时的计算格式称为显式格式。当0＜θ≤1时，新时刻的结点温度值也被用于求解TP，此时的计算格式称为隐式格式。其中，当θ=1时的格式称为全隐格式，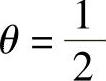
时的格式称为CrankNicolson格式（简称CN格式）。下面简要讨论θ=0，θ=1和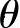
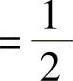时的离散方程的具体形式。
2.显式计算格式
显式计算格式中源项可线性化处理为b=Q0+QPT0P，此时将θ=0代入方程式（4.11.13），可得非稳态扩散问题的显式离散方程为
aPTP=aWT0W+aET0E+[a0P-（aW+aE-QP）]T0P+Q0 （4.11.14）
式中，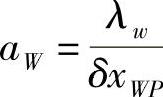
；
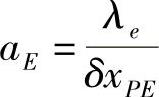；aP=a0P；
。
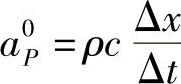方程式（4.11.14）右端只包含前一时间层的温度值，因此左端TP可按时间步向前推进解出。按有限差分理论，这种格式属于向后差分时间近似，计算精度只有一阶截差。按照离散方程有界性的要求，方程式（4.11.14）中所有系数应为正值。因此应有（a0P-aW-aE）＞0。若λ为常数，并且采用均匀网格系统，即δxWP=δxPE=Δx，则上述条件可写成
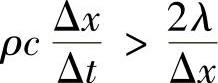
或
式（4.11.15）对显式格式的计算时间步长Δt的最大值给出了一个相当严格的限制。这将导致实际计算时为提高计算精度而花费巨大的代价，因为最大可能时间步长随着网格空间尺度的减小而减小。因此，显式格式并不适合于计算一般情况下的非稳态问题，但当计算时间步长满足式（4.11.15）的要求时，将显式格式用于计算简单扩散问题还是有效的。
3.CrankNicolson格式
将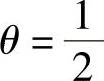
代入方程式（4.11.13），并将源项线性化处理b=Q0+QPT0P/2，可得非稳态热传导问题CrankNicolson格式离散方程。
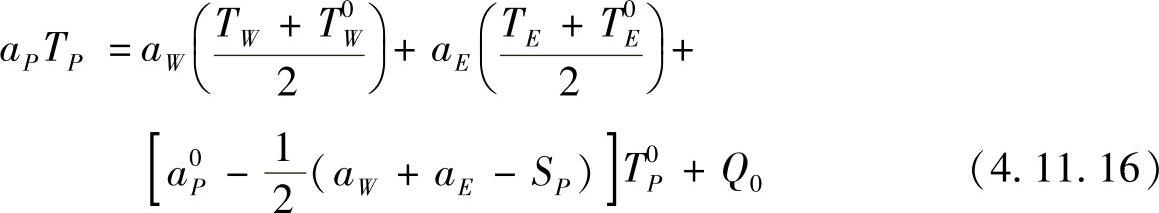
式中，
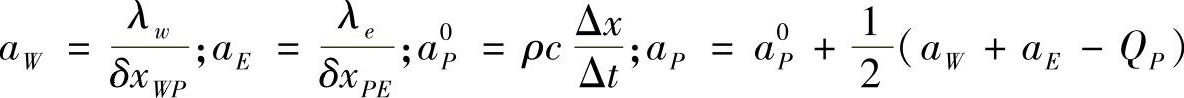
从方程式（4.11.16）可以看出，下一时间步有多个结点温度值出现在方程式中。因此，在每一时间步必须同时求出所有结点温度值，故称为隐格式。尽管对于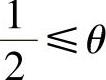
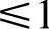的隐式格式，包括CrankNicolson格式，计算是无条件稳定的，但从方程系数有界性要求考虑，为保证所有系数为正值，源项为零时，T0P的系数应满足
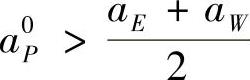
即
这一时间步长限制只比显式格式时间步长限制稍有放松，对计算的空间和时间尺度的要求仍然较严。本质上，CN格式是对时间中心差分，计算精度可达二阶截差。因此当Δt足够小且满足式（4.11.17）时，CN格式可获得比显式格式计算结果更高的精度。
4.全隐格式
当θ=1，源项作线性化处理b=Q0+QPTP时，由方程式（4.11.13）可得全隐格式非稳态热传导问题离散方程，即
aPTP=aWTW+aETE+a0PT0P+Q0 （4.11.18）
式中，
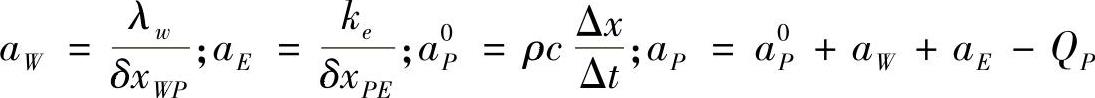
方程式（4.11.18）两端都出现下一时刻的温度，因此求解时要先给出初始温度分布T0。在t+Δt时刻求解，其结果再赋予T0，然后进行时间推进，下面将通过算例来说明求解过程。
从式（4.11.18）中可看出，所有系数保持正值，因此，全隐格式对任意时间步长Δt都是无条件稳定的，但计算精度只有一阶截差，为保证计算精度，还是应选择较小的时间步长。全隐格式由于无条件稳定和收敛性好，被广泛用于各种非稳态问题的求解过程中。
【例4.11.1】一无限大薄板，初始状态为均匀温度200℃，在某一时刻t=0，板东侧面温度突然降至0℃，西侧面保持绝热。板厚L=0.02m，导热系数λ=10W/（m·K），ρc=10×106J/（m3·K）。试分别采用显式格式和全隐格式，选择合理的时间步长，计算t=40s时板的温度分布。
【解】定解问题为
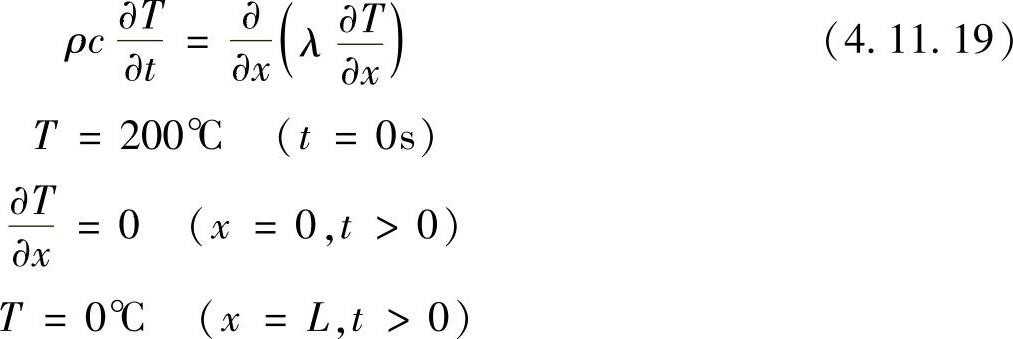
将计算区域划分为5个相等的控制容积，每个控制容积长Δx=L/5=0.004m，如图4.11.1所示。
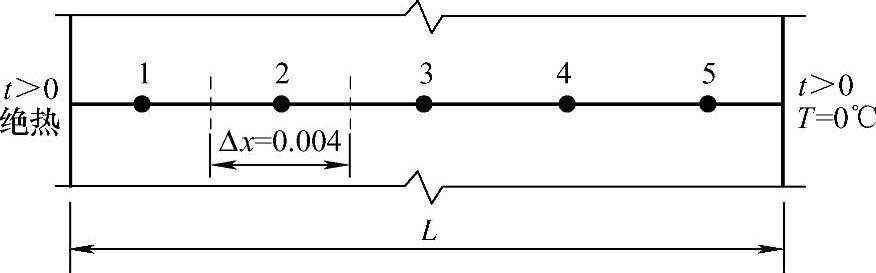
图4.11.1 计算域网格划分
（1）采用显式格式计算
本例内结点2～结点4的离散方程为式（4.11.14），结点1和结点5为边界结点，需特殊处理。
对于结点1，控制容积西侧界面绝热，因此穿过此界面的热流为零。据此物理意义修正方程式（4.11.11），有θ=0，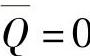
，λw=0，于是，有
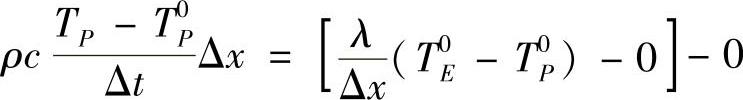
或(www.daowen.com)
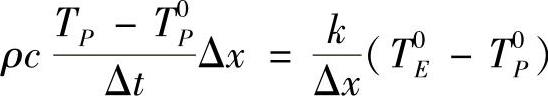
对于结点5，当t＞0时东侧界面温度TB为常数，离散方程成为
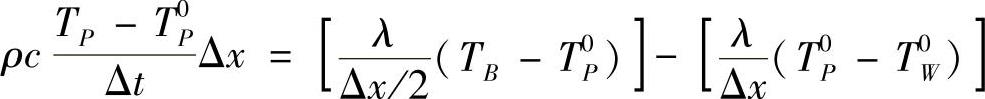
所有结点的控制容积离散方程统可写为
aPTP=aWT0W+aET0E+[a0P-（aW+aE-QP）]T0P+Q0
式中各结点的系数见表4.11.1。
表4.11.1 离散方程系数
显式格式稳定计算时间步长极限值为
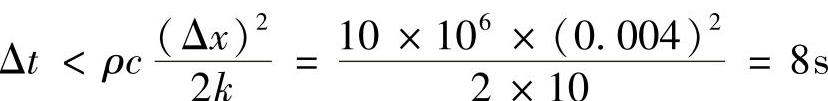
若取Δt=2s，则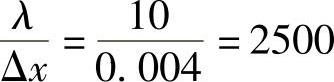
，
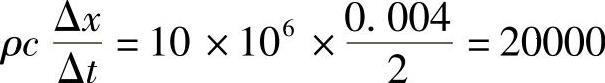，将这些数据及TB=0代入方程式（4.11.4），可得各结点离散方程。
对于结点1，有
200TP=25T0E+175T0P
对于结点2，3和结点4，有
200TP=25T0W+25T0E+150T0P
对于结点5，有
200TP=25T0W+125T0P+50T0B
求解此方程组可得所希望的结果，前三个时间步的计算过程列于表4.11.2中。
表4.11.2 离散方程系数
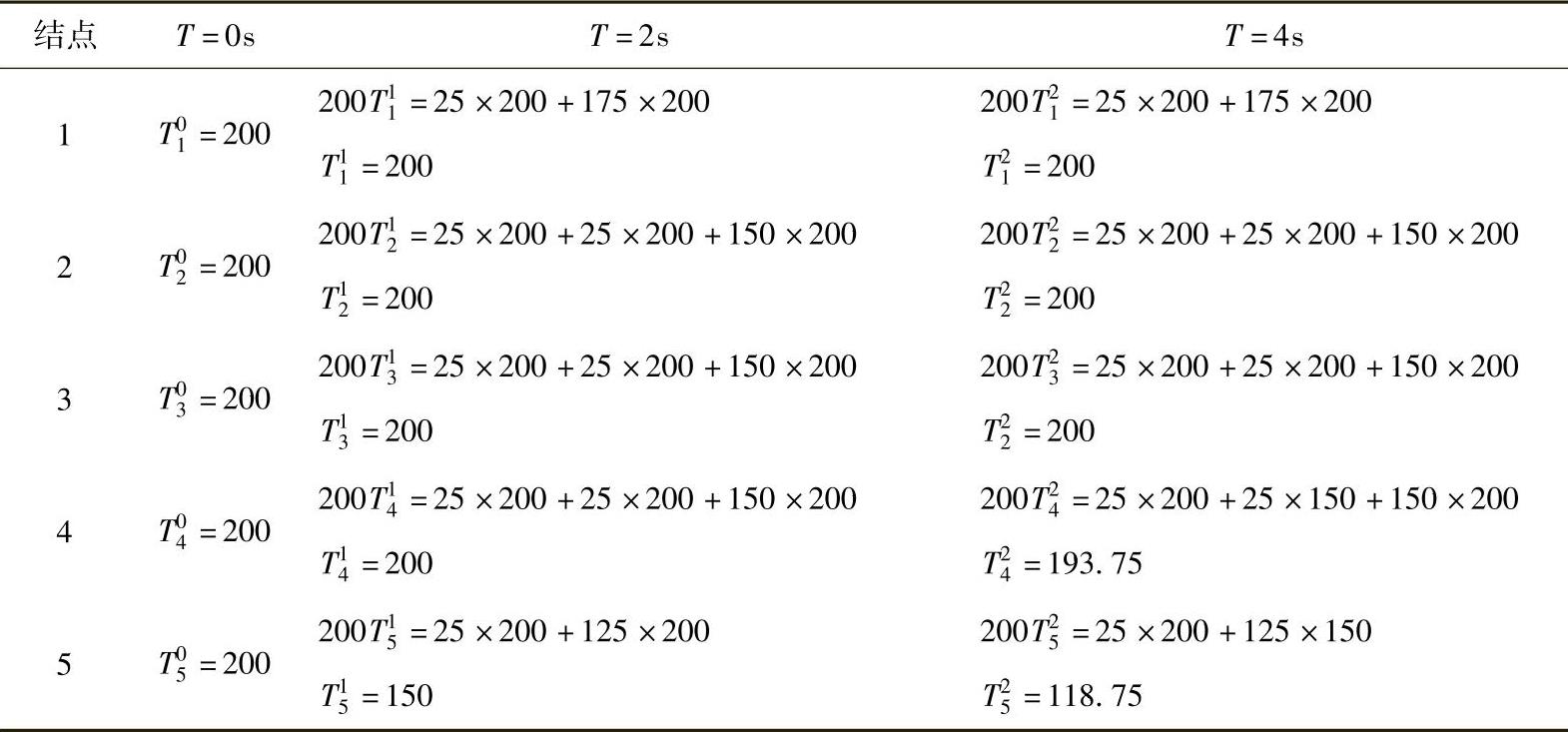
在表4.11.2的中Tβα，下脚标α表示结点号，上角标β表示时间步，计算过程尽管不复杂，但比较繁琐，需编程上机计算。
若将时间步长加大到Δt=8s时，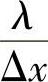
仍为2500，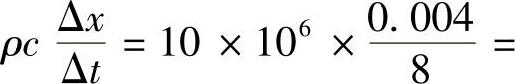
。
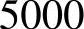对于结点1，有
50Tp=25T0E+25T0P
对于结点2，3和结点4，有
50TP=25T0W+25T0E
对于结点5，有
50TP=25T0W-50T0P+50TB
通过编程上机计算可得，Δt=8s的数值计算结果精度低，并产生振荡，因此，时间步长的减小可有效地提高数值计算结果的精度。
（2）采用全隐格式
内结点2，3和结点4的全隐格式离散方程为式（4.11.18），边界结点的控制容积积分需特殊处理。我们将边界条件代入方程式（4.11.11），可得
对于结点1，有
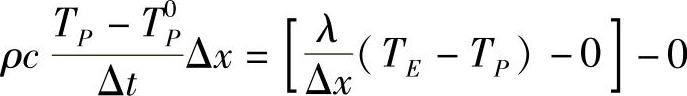
对于结点5，有
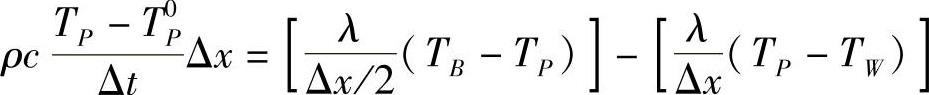
离散方程的标准形式仍为
aPTP=aWTW+aETE+a0PT0P+Q0
式中各结点的系数见表4.11.3。
表4.11.3 离散方程系数
尽管全隐格式对任意时间步长都是无条件稳定的，但为了保证计算精度，希望采用尽可能小的时间步长，这里取Δt=2s，于是
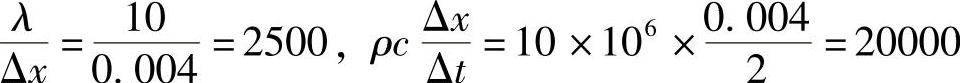
对于结点1，有
225TP=25TE+200T0P
结点2，3和结点4，有
250TP=25TW+25TE+200T0P
对于结点5，有
275TP=25TW+200T0P+50TB
由于TB=0，整理可得下列方程组
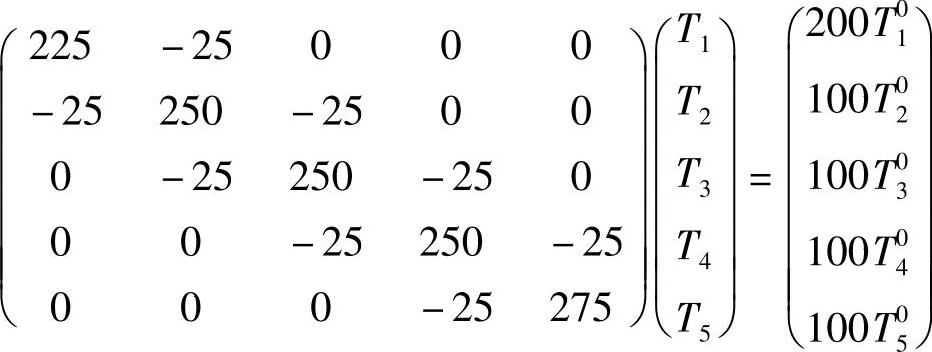
可以看到，方程组中每一个方程都包含有未知的邻点温度，而显式格式方程中只包含前一时间层解出的温度，因此，直接由代数方程组可求出本时间层任一点温度。全隐格式必须在每一时间层求解方程组，上一时间层的温度值只用于计算方程组右端项，因此，求解过程更费时。当时间步长较大时，例如，若本例题取Δt=8s，显式格式数值解的精确度差且产生振荡，而全隐格式的数值解则比较接近精确解，这表明了全隐格式的突出优点，即可以“容忍”较大的时间推进步长。但是应强调一点，步长过大将影响计算结果的精度。因此在可能的条件下，还是应选择尽可能小的时间步长计算，以上工作请读者自行完成。
5.高维非稳态扩散问题全隐格式
全隐格式无条件稳定，计算精度也较高，因此是求解一般非稳态扩散问题的推荐算法。一维非稳态扩散问题全隐格式可推广到高维扩散问题计算中。
三维非稳态扩散问题的控制方程为
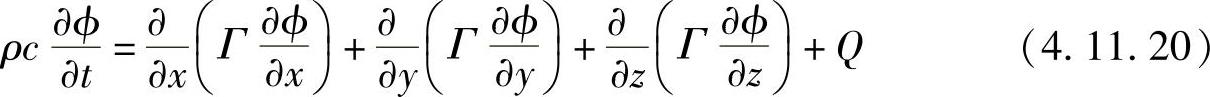
对其在控制容积中积分并仿照一维问题推导过程，可得下述离散方程
aPϕP=aWϕW+aEϕE+aSϕS+aNϕN+aTϕT+aBϕB+a0Pϕ0P+Q0 （4.11.21）
式中，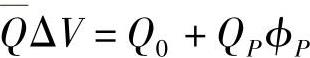
，各系数的值见表4.11.4。
表4.11.4 对流扩散问题离散方程系数
对式（4.11.21）右端的离散与扩散问题一样，只是等号左端与时间有关，在离散后出现与时间有关的项a0Pϕ0P，主结点场变量系数的计算式中也只多一项a0P。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
