二维问题有限体积法得到的离散方程其通式为

a_Pϕ_P=a_Wϕ_W+a_Eϕ_E+a_Sϕ_S+a_Nϕ_N+b （4.10.16）

为使TDMA算法能够应用，需将方程式（4.10.16）转换成通用形式，转换的方式有两种

-a_Sϕ_S+a_Pϕ_P -a_Nϕ_N=a_Wϕ_W+a_Eϕ_E+b （4.10.17）

或(www.daowen.com)

-a_Wϕ_W+a_Pϕ_P -a_Eϕ_E=a_Sϕ_S+a_Nϕ_N+b （4.10.18）式（4.10.17）和式（4.10.18）等号左侧已经成为三对角方程的标准形式，等号右侧可认为是通用形式中的C_j，即认为暂时已知，这样就可利用TDMA算法求解方程组。但实际上C_j是未知的，方程组经过一轮消元和回代得到的ϕ_S，ϕ_P和ϕ_N（或ϕ_W，ϕ_P和ϕ_E）不可能是真实解，而且计算结果中也未求出ϕ_W和ϕ_E（或ϕ_S和ϕ_N）。因此要反复迭代求解才有可能求出真解。迭代过程如图4.10.3所示。首先选择一个计算方向，即相当于一维问题的计算，图4.10.3是先选南北方向线计算，这样我们就采用式（4.10.17）来计算。

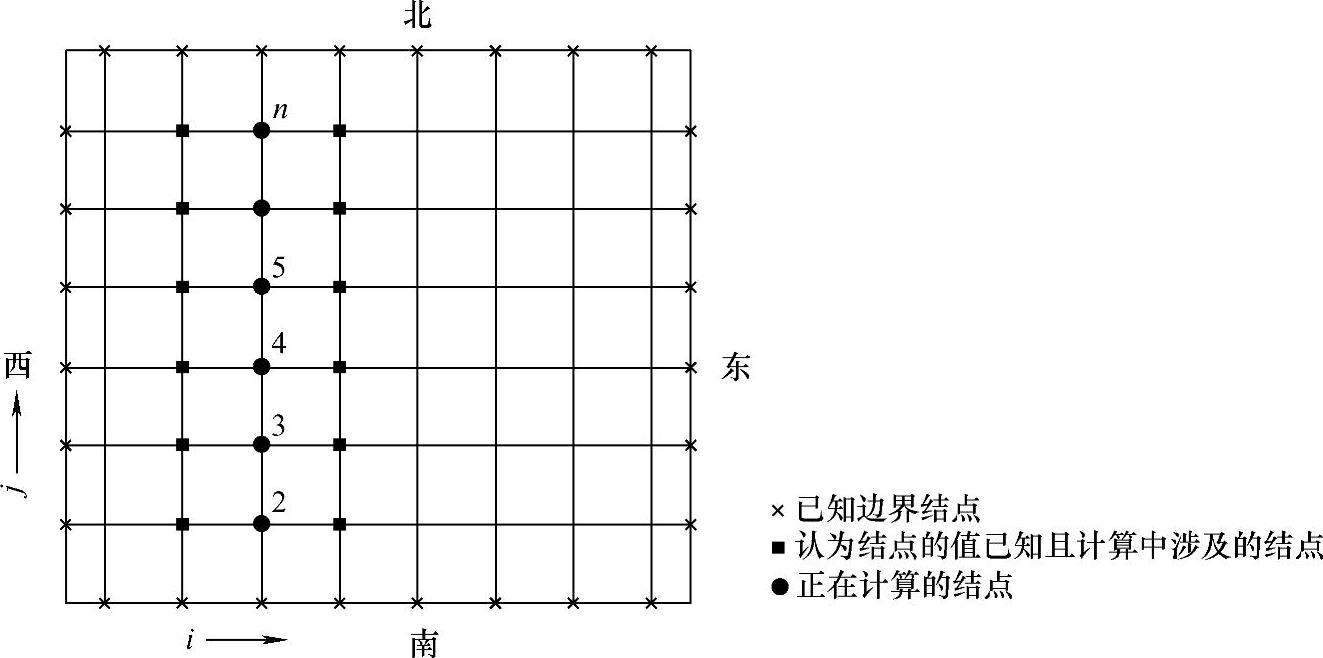
图4.10.3 二维问题应用TDMA算法逐线迭代过程示意

首先沿一根南北方向线计算线上各点2，3，4，…，n的方程，计算中暂时认为所涉及的东西侧结点上的值为已知。求解完一条南北方向线上所有结点的方程后，沿东西方向移动到下一条南北方向线，依原样计算。这时SN线西侧结点处的ϕ值可利用刚刚计算出的结果，而东侧结点值还是假设值或上次迭代结果，扫过所有南北方向线之后，就得到了所有结点上的场变量值，但其结果一般来讲不是真实解，因此，还需要反复实行上述计算过程，使结点场变量值逐渐逼近真解。