设有下列三对角方程
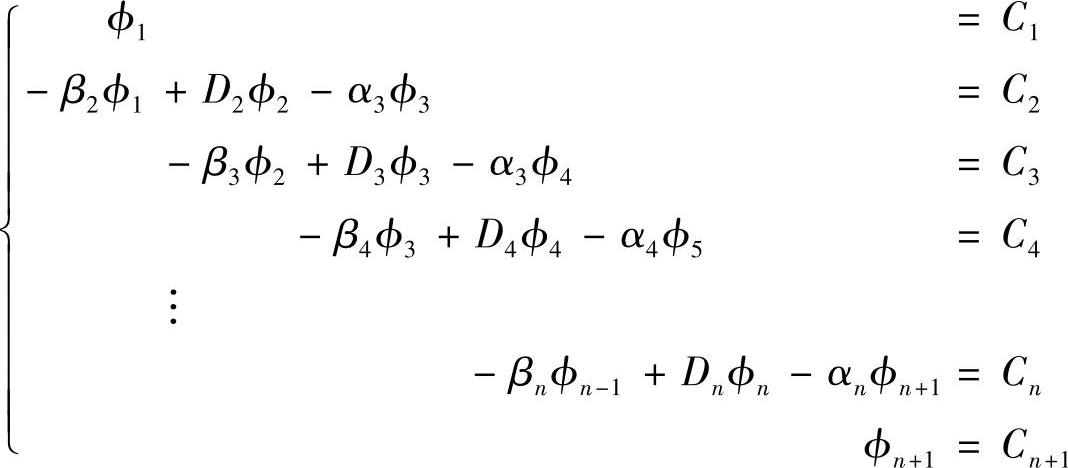
方程组中的ϕ1和ϕn+1作为边界条件是已知的,方程组中任意一个方程的通用形式为
-βjϕj-1+Djϕj -αjϕj+1=Cj
将方程组以上述通用形式写为
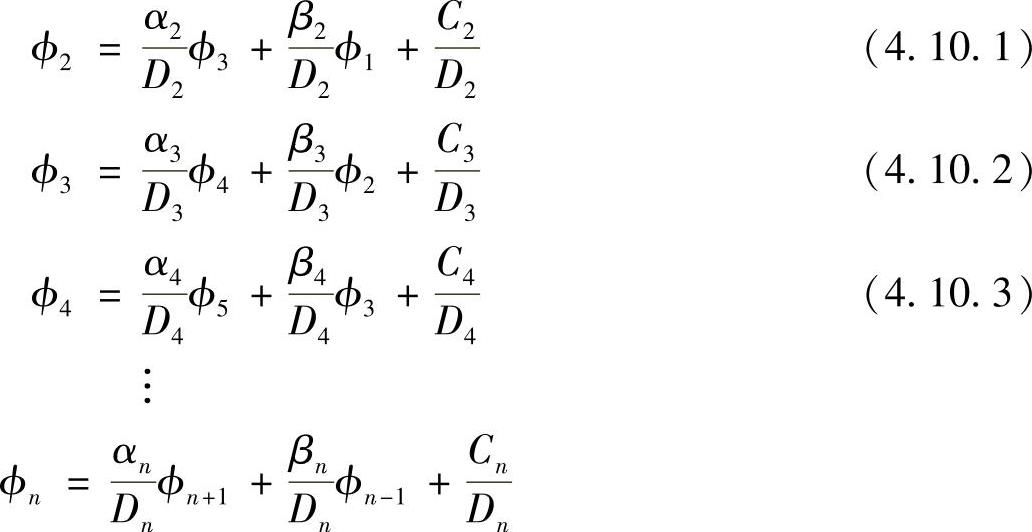
该方程组可通过向前消元和向后回代两个过程来求解,向前消元过程从消去ϕ2开始,将式(4.10.1)代入式(4.10.2),得
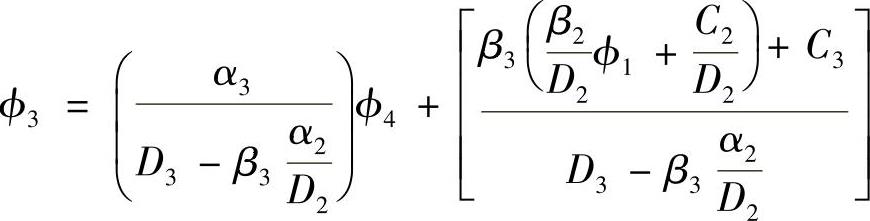
令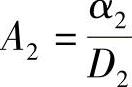 ,
,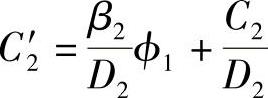 ,则有
,则有
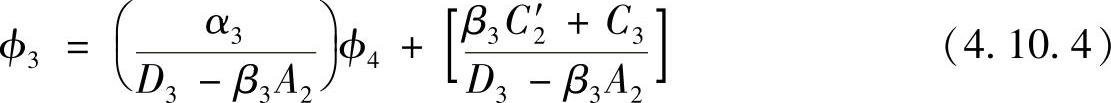
再令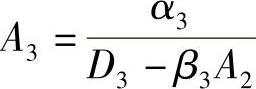 ,
,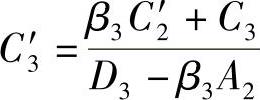 ,则有
,则有
ϕ3=A3ϕ4+C3′ (4.10.5)
利用式(4.10.5)可从式(4.10.2)中消去ϕ3,同时这一过程可一直做下去直至最后一个方程中的ϕn-1被消去。
回代过程用式(4.10.5)的通用形式,即
ϕj=Ajϕj+1+Cj′ (4.10.6)
式中,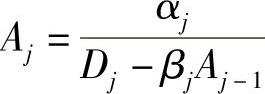 ;
;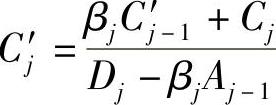 。
。
利用边界条件,当j=1和j=n+1时的已知值,求A1和C′1以及An+1和Cn′+1,即
A1=0,C′1=ϕ1,An+1=0,Cn′+1=ϕn+1
消元到最后一个方程时,有ϕn=Anϕn+1+Cn′,而ϕn+1为已知边界条件。根据An和Cn′就可求出ϕn,有了ϕn可进一步求出ϕn-1,一直求到最前面的ϕ值,这一过程称为回代。
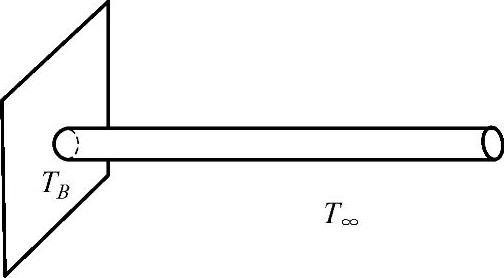
图4.10.1 算例4.10.1图
【例4.10.1】图4.10.1所示圆截面棒,截面积为S,长度L=1m,棒根温度TB=100℃,环境温度T∞=20℃,棒端绝热,棒通过环境向外对流散热,对流换热系数为h,材料导热系数为λ,肋条周长为c,用数值方法计算棒沿长度方向的温度分布。已知该一维导热问题的控制方程为
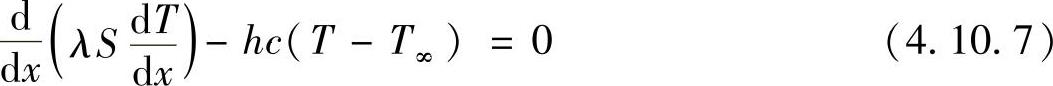
式中,n2=hc/(λA)。已知hc/(λS)=25m-2,λS=常数。
【解】首先将肋条全长划分成5个均匀控制容积,每个控制容积长δx=0.2m,网格如图4.10.2所示。
当λA为常数时,可将此问题控制微分方程改写为
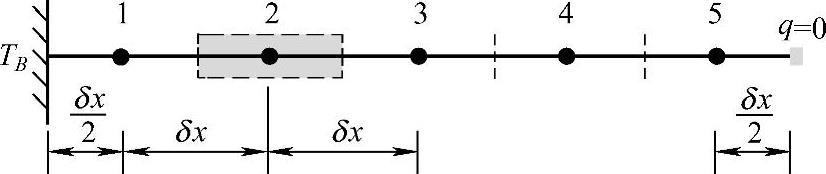
图4.10.2 网格划分
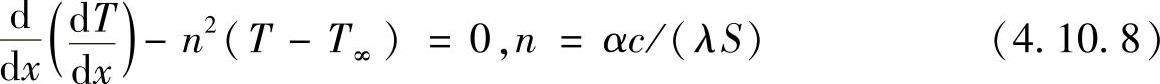
对方程式(4.10.8)在控制容积中积分
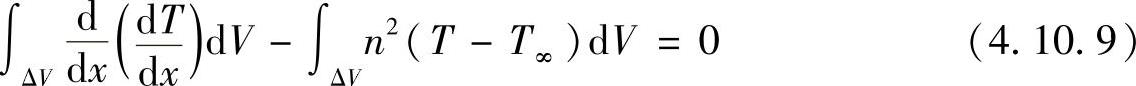
式中,第一项为扩散流,第二项可看成源项,若假设被积函数在控制容积中温度保持不变,有
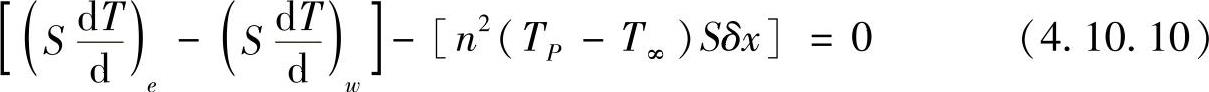
在结点2、结点3和结点4可写出离散方程为
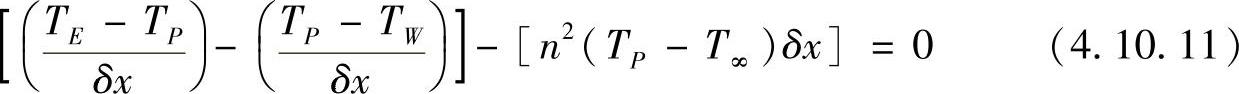
整理,得
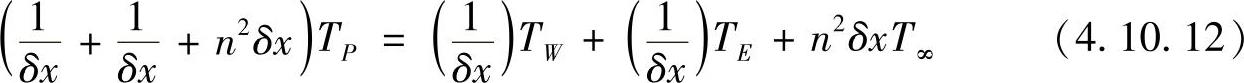
对内结点下述方程成立(https://www.daowen.com)
aPTP=aWTW+aETE+Q0 (4.10.13)
式中,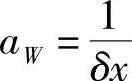 ;
;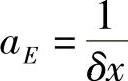 ;aP=aW+aE-QP;QP=-n2δx;Q0=n2δxT∞。在结点1,控制容积西侧界面保持常温,因此
;aP=aW+aE-QP;QP=-n2δx;Q0=n2δxT∞。在结点1,控制容积西侧界面保持常温,因此
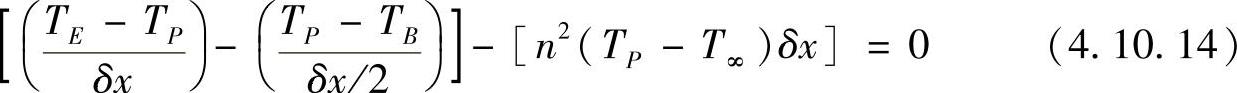
整理,可得结点1的离散方程系数为
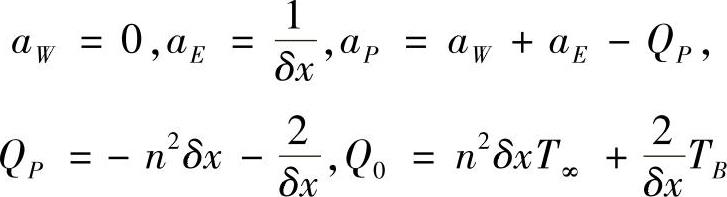
在结点5,流过边界的热流量为零,采用类似的推导,可得结点5的离散方程为
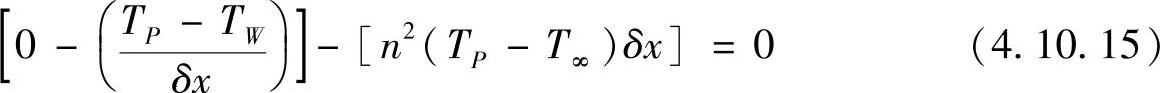
整理可得结点5的离散方程系数为
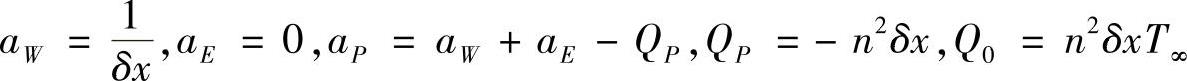
将已知数据代入,得各结点方程系数,见表4.10.1。
表4.10.1 离散方程系数

写成矩阵形式的离散方程组为

下面用TDMA算法解该方程组。由通用方程表达式,即
-βjTj-1+DjTj -αjTj+1=Cj
在结点1和结点5,β1=0,α5=0,边界T是未知的,边界条件是由Cj引入的。为使计算结果清楚,将系数β,D,α,C和计算值A,C′列于表4.10.2中。Aj和Cj′的计算公式和计算过程列于表4.10.3中。
表4.10.2 方程组系数
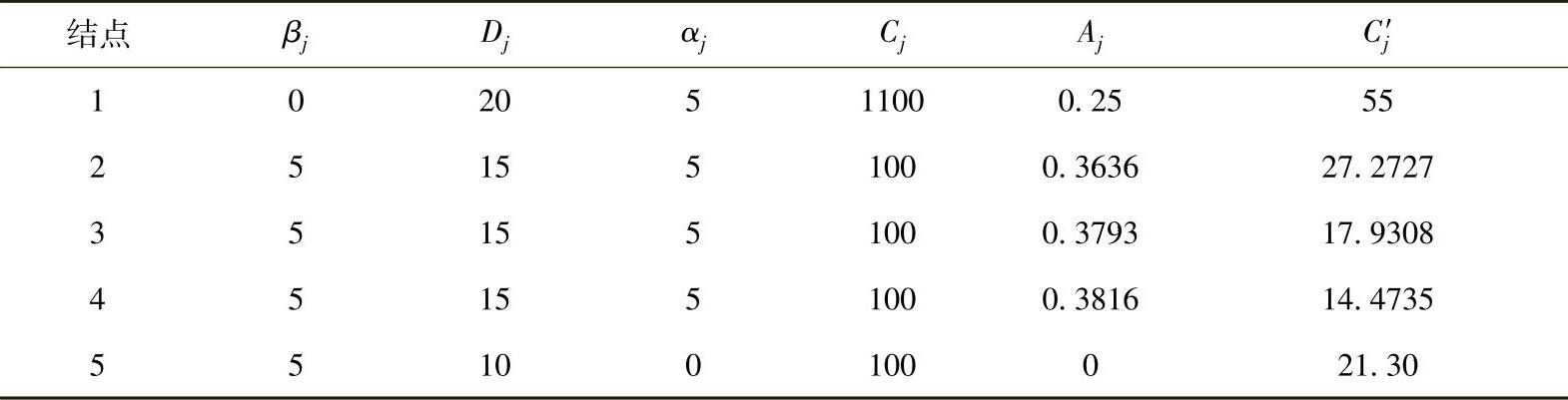
表4.10.3 Aj和Cj′的计算公式和计算过程

(续)

由Aj和Cj′可写出消元后的结果,其通式为
Tj=AjTj+1+Cj′
于是
T2=0.3636T3+27.2727
T3=0.3793T4+17.9308
T4=0.3816T5+14.4735
T5=21.30
回代过程为
21.30=T5
0.3816×21.30+14.4735=22.60=T4
0.3793×22.60+17.9308=26.50=T3
0.3636×26.50+27.2727=36.91=T2
0.25×36.91+55=64.22=T1
经过一个消元过程和一个回代过程,得到最后结果,TDMA算法占用很少的计算机资源,具有很高的计算效率,但仅适宜计算三对角代数方程。有限体积法中一维问题的高阶差分格式和二维、三维问题得到的离散方程并非三对角方程,每一个代数方程有5个或7个非零系数,因此TDMA算法不能直接应用,但由于TDMA算法计算效率高,我们仍希望能将TDMA算法应用于求解高维有限体积法离散方程。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。








