SIMPLER算法是建立在SIMPLE算法基础上的一种改进算法（SIMPLE Revised），其基本思想是利用假设的或前次迭代得到的速度场直接求出一个中间压力场，用来代替假设的压力场，而由压力修正方程得到的压力改进量p′用于修正速度，压力则由速度根据连续性方程推导出压力方程计算。SIMPLER算法整个过程为先将离散动量方程式（4.9.12）和式（4.9.13）改写为

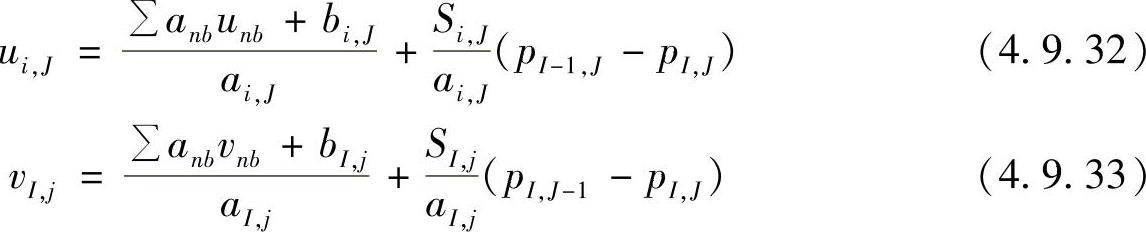
假设速度分布之后，上两式右端第一项可算出，这一项显然具有速度的量纲，SIMPLER算法中定义它为假拟速度或伪速度（pseudovelocities），即

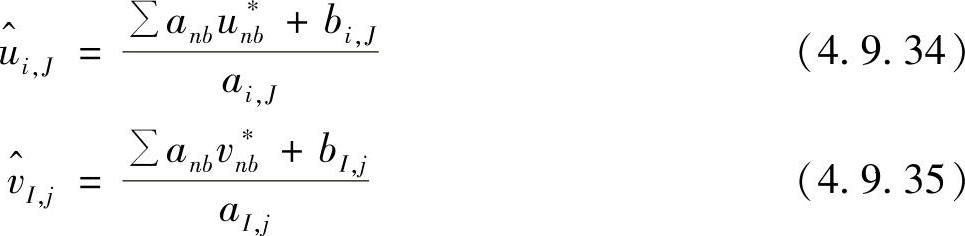
这时，式（4.9.32）和式（4.9.33）可写成

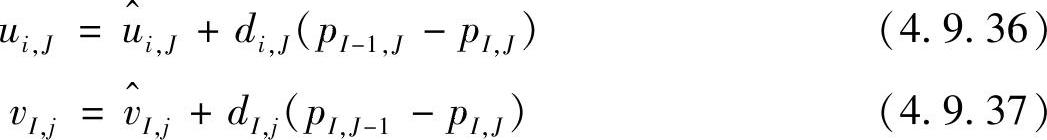
同理，可写出

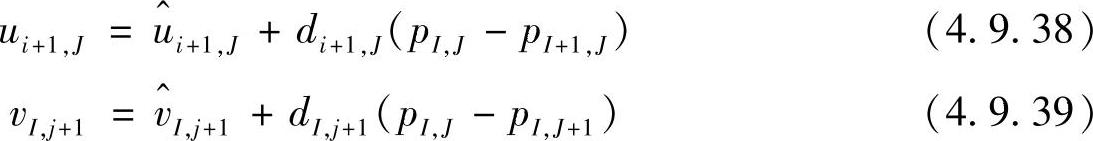(www.daowen.com)

d项的定义如前所述。将式（4.9.36）～式（4.9.39）代入连续性方程式（4.9.12），有

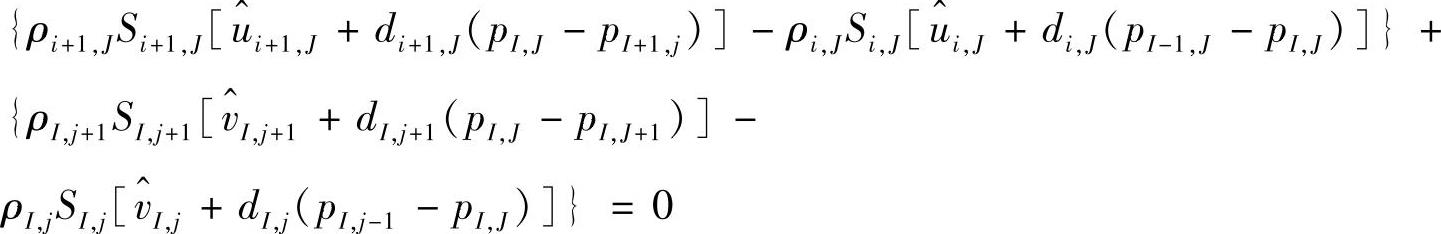
按结点压力值整理并对系数作归一化处理，可得

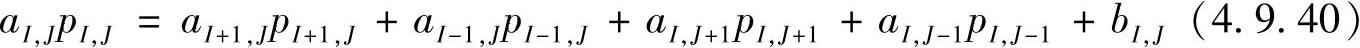
式中，

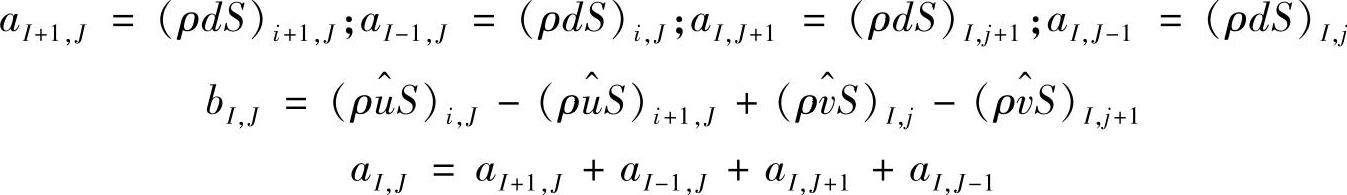
方程式（4.9.40）即为计算中间压力的压力计算方程，其形式与压力修正方程式（4.9.24）完全一致，只是源项b的计算方法不同，此处采用伪速度值。从上述推导过程可知，利用伪速度值按照式（4.9.40）可计算出压力分布p，由压力场根据动量方程可求出速度分布u与v，再由压力修正方程式（4.9.24）可计算压力修正量p′，利用p′由式（4.9.36）～式（4.9.39）计算速度场改进值，进而循环迭代。SIMPLER算法可用图4.9.8所示框图表示其计算流程。