
为解决连续性方程离散时所遇到的困难可采用压力预测修正方法,即所谓的SIMPLE算法,它是通过不断修正计算结果,反复迭代,最后求出p,u,v的收敛解。SIMPLE算法的基本思想是先假设一个压力分布p∗,利用它求解动量方程式,得到初始速度分布u∗和v∗,即
ai,Jui∗,J=∑anbun∗b+(pI∗-1,J-pI∗,J)Si,J+bi,J (4.9.12)
aI,jvI∗,j=∑anbvn∗b+(pI∗,J-1-pI∗,J)SI,j+bI,j (4.9.13)
上述方程等号右端的速度un∗b和vn∗b也是初始假设值,等号左端的速度才是计算得到的初始速度分布,一般来讲,这样求得的速度场u∗和v∗不能满足连续性方程,压力p∗也仅仅是一个假设分布,因此,需要对压力p∗和速度u∗,v∗进行修正。
设压力修正量为p′,速度修正量为u′,v′,修正后的压力和速度计算公式可写为
p=p∗+p′
u=u∗+u′
v=v∗+v′
下面的问题是如何求出修正量p′,u′和v′。这里先假设已经知道压力场p的正确值,将p代入方程式(4.9.8)和式(4.9.9),可解得速度场的正确值u,v。这时将方程式(4.9.8)减去方程式(4.9.12),即u-u∗=u′,将方程式(4.9.9)减去方程式(4.9.13),即v-v∗=v′,得到速度修正量的表达式为
ai,J(ui,J-ui∗,J)=∑anb(unb-un∗b)+[(pI-1,J-pI∗-1,J)-(pI,J-pI∗,J)]Si,J (4.9.14)
aI,j(vI,j-vI∗,j)=∑anb(vnb-vn∗b)+[(pI,J-1-pI∗,J-1)-(pI,J-pI∗,J)]SI,j (4.9.15)
于是,有
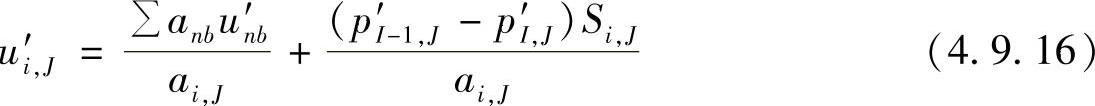
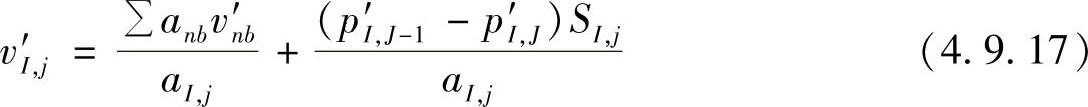
速度修正量u′和v′由两项构成,从物理意义上讲,前一项是由周围结点速度所引起的修正量,后一项是由同一方向相邻结点压力差引起的修正量。为简单计算,这里略去第一项的影响。从而速度修正量可写为

式中,
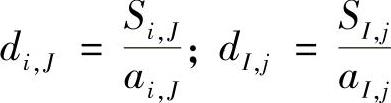
有了速度修正量就可得到速度的改进值为
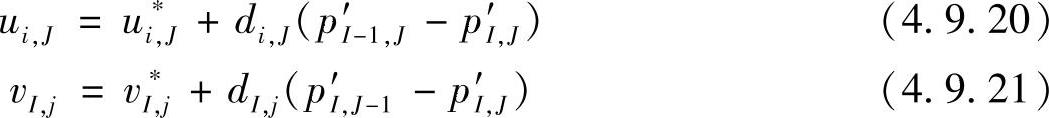
由图4.9.6可以看出,式(4.9.20)和式(4.9.21)表示的速度是主控制容积西侧界面的x方向速度改进值和南侧界面y方向速度改进值。同理,可写出北侧界面y向速度改进值vI,j+1和东侧界面x方向速度改进值ui+1,J为
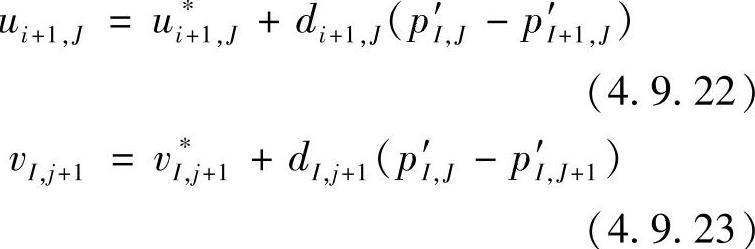
式中,
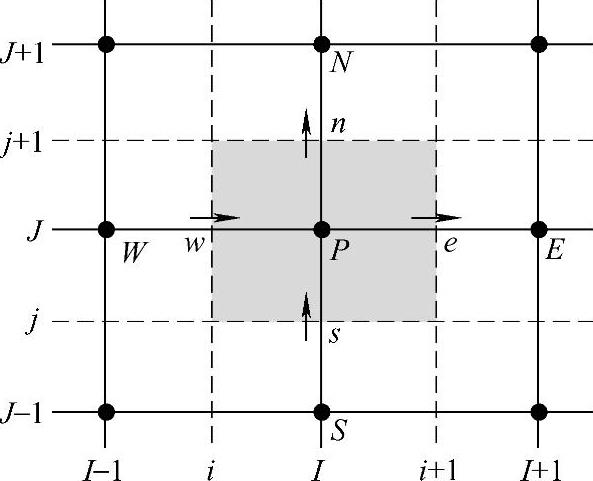
图4.9.6 主控制容积与连续性方程离散
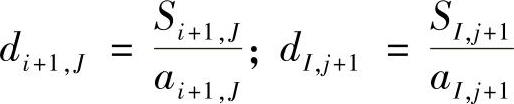
以上我们从动量方程出发,得到了速度改进值,而由动量方程计算出的速度场必须满足连续性方程。将式(4.9.20)~式(4.9.23)计算得到的速度改进值代入连续性方程(4.9.10),有
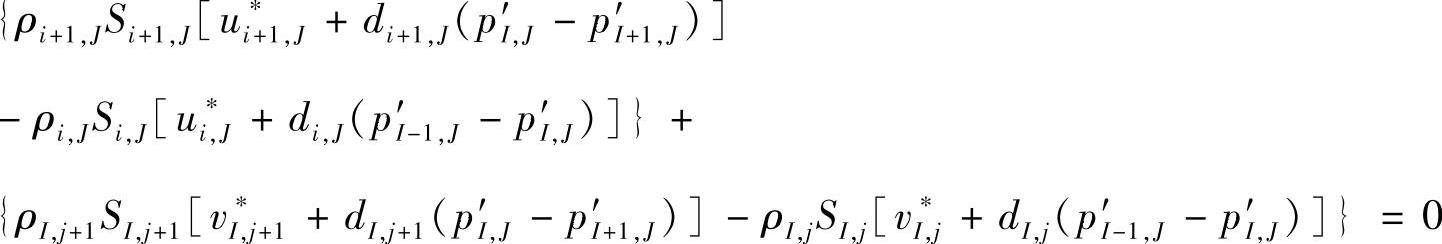
整理,得
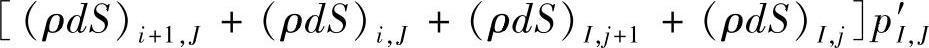 (www.daowen.com)
(www.daowen.com)
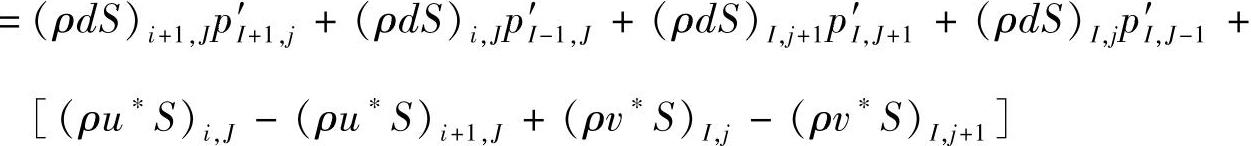
将压力修正量p′的系数归一化处理,就得到压力修正方程
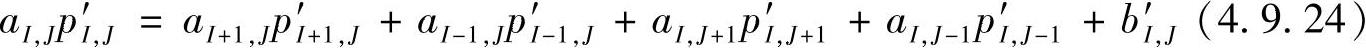
式中,
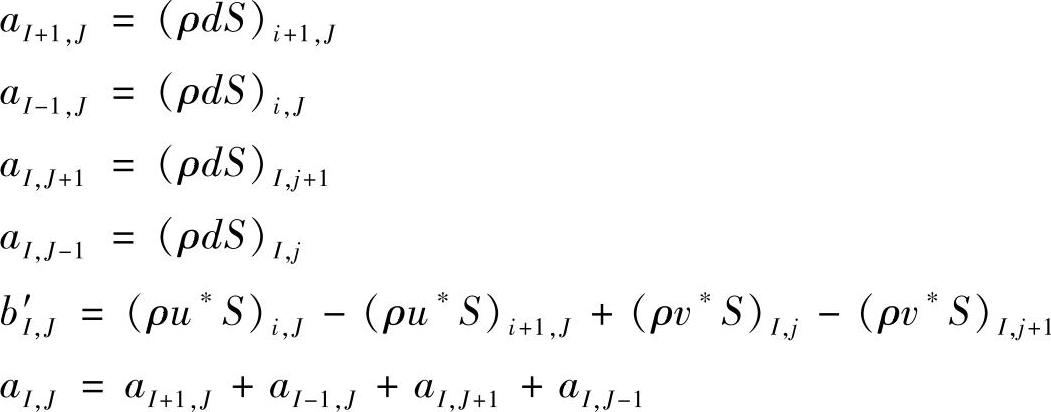
式(4.9.24)是由连续性方程导出的压力修正方程,其中,源项b′的物理意义是,由于速度场的不正确引起的不平衡流量,通过多次迭代修正,最终b′应趋于零。因此,b′可作为判断迭代过程是否满足要求的判据。根据假设的或前次迭代计算得到的速度场,通过求解压力修正方程式(4.9.24)可得压力修正量p′,由此以及式(4.9.20)~式(4.9.23)可得压力和速度的改进值,之后可进行下一层次的迭代计算。SIMPLE算法的计算流程如图4.9.7所示。
应当指出,前面在推导速度场修正量的方程时,忽略了方程式(4.9.16)和式(4.9.17)的第一项,即由周围结点速度引起的修正量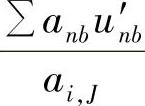 和
和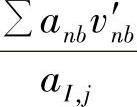 ,这样做并不会影响最后的计算结果,因压力修正量p′以及速度修正量u′和v′在迭代最后所得到的收敛解都将趋于零,即最后结果是p=p∗,u=u∗,v=v∗。此外,若相邻两次迭代过程中压力修正量过大,压力修正方程求解时会出现发散现象,特别是在上一层次迭代压力值距真实值较远的情况下。因此,下一层次的压力改进值要采用亚松弛因子计算得出,即
,这样做并不会影响最后的计算结果,因压力修正量p′以及速度修正量u′和v′在迭代最后所得到的收敛解都将趋于零,即最后结果是p=p∗,u=u∗,v=v∗。此外,若相邻两次迭代过程中压力修正量过大,压力修正方程求解时会出现发散现象,特别是在上一层次迭代压力值距真实值较远的情况下。因此,下一层次的压力改进值要采用亚松弛因子计算得出,即
pn=pn-1+αPp′ (4.9.25)
式中,pn为新迭代层的压力改进值;pn-1为前一迭代层的压力值;αp为压力松弛因子,0≤αp≤1。αp=1意味着pn=pn-1+p′,压力改进量全部加入修正值中,我们在计算中希望αp值尽可能大,以加快收敛,但又不引起计算过程不稳定。
通常速度计算也需要采用亚松弛迭代,速度的迭代改进值为
un=un-1+αuu′=un-1+αu(u-un-1) (4.9.26)
同理,
vn=vn-1+αv(v-vn-1) (4.9.27)
式中,un-1和vn-1为上一层次计算所得速度值;u和v为本层次计算所得未经亚松弛处理之值,un和vn为亚松弛处理后的本层次计算值,αu,αv为松弛因子,取值仍在0和1之间。
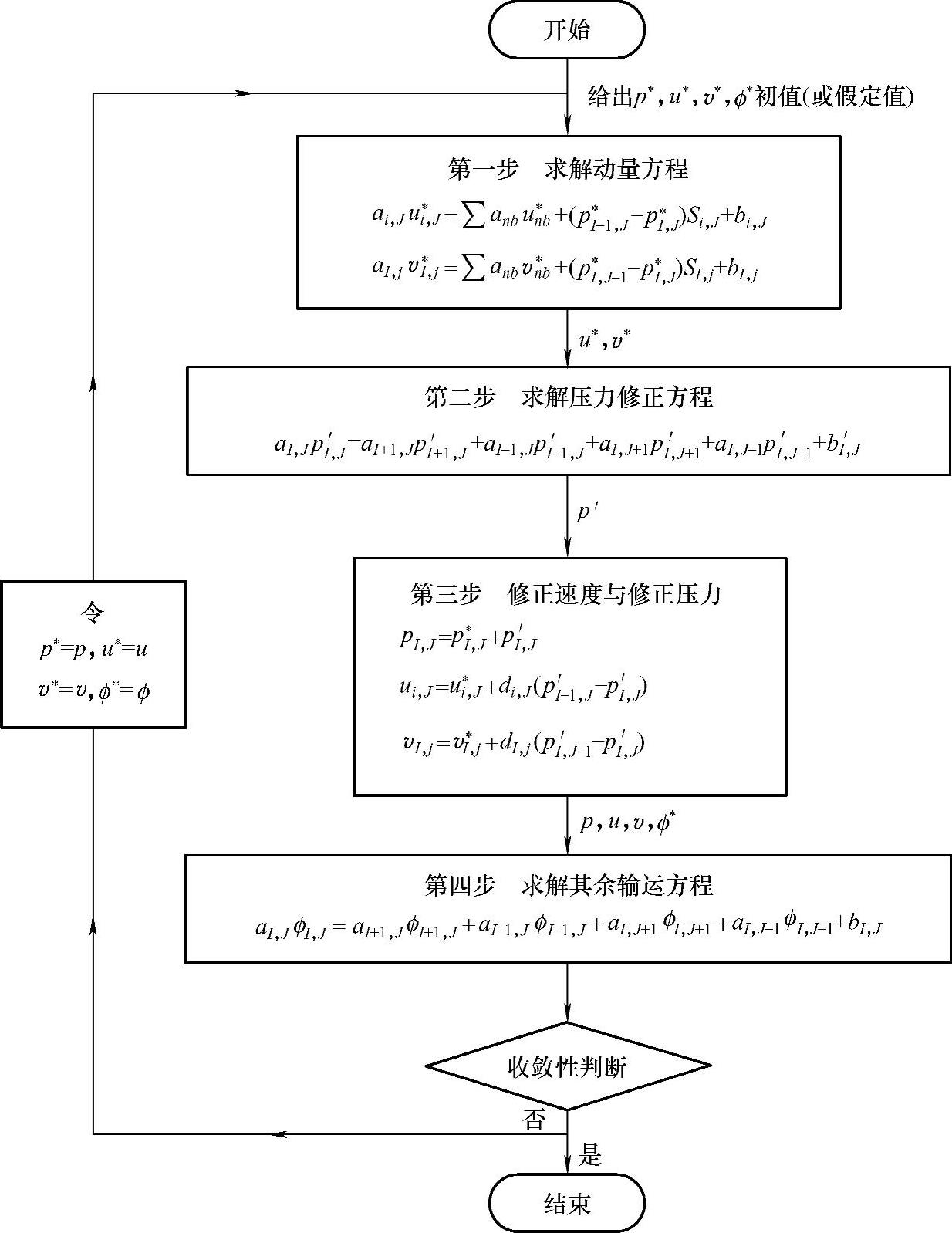
图4.9.7 SIMPLE算法的计算流程
由式(4.9.26)可得

将动量方程离散方程式(4.9.8)改写为
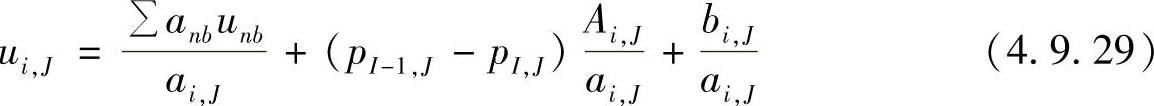
式(4.9.28)应等于式(4.9.29),因此有
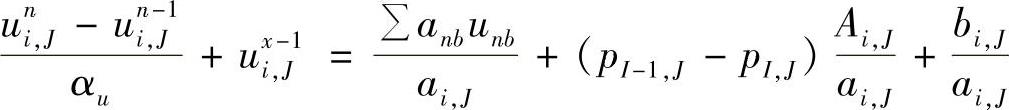
整理,得
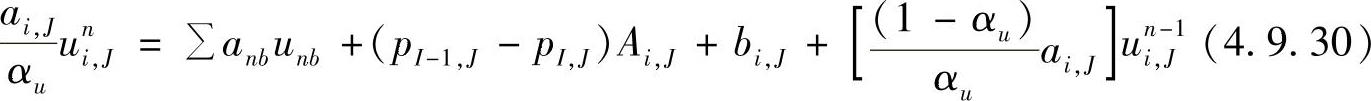
同理,
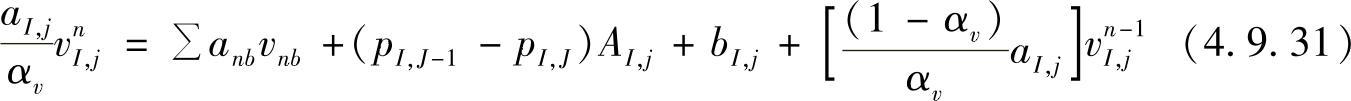
由于速度采用亚松弛迭代,压力修正方程式(4.9.24)也要受到影响。式(4.9.24)中各系数的d分量变成
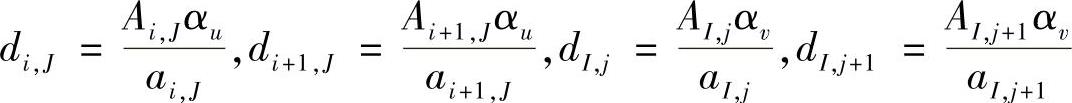
利用式(4.9.30)、式(4.9.31)和改进系数后的压力修正方程就可进行亚松弛条件下的压力和速度迭代计算,但亚松弛因子的大小并没有办法确定其最优值,它与流体流动状况有关,通常只能在计算中通过数值实验取值。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





