1.交错网格布置方式

在同样的网格点上不一定要计算所有的变量，可以对每一个因变量采用不同的网格系统。如果把速度分量各自放在与其他所有变量不同的网格上，会使上述的困难完全消失。交错网格是将标量型变量，如温度、浓度等的网格系统与矢量型变量u_i的网格系统错开，也就是将压力与速度耦合方程中不同的变量存储在不同的网格系统中。我们把以结点为中心的控制容积称为主控制容积，将压力存储在主控制容积的结点中心，而将速度按其方向存储在与主控制容积相差半个网格步长的错位的控制容积中。以二维问题为例，图4.9.3中结点周围的控制容积为计算压力p的主控制容积，水平方向与主控制容积错位半个网格的控制容积为计算x方向速度u的控制容积，垂直方向与主控制容积错位半个网格的控制容积为计算y方向速度v的控制容积。水平方向箭头位置表示u速度计算点位置，垂直方向箭头表示v速度计算点位置。于是u，v和p存储在三种不同控制容积的网格系统中，各网格位置相互交错，即网格交错。采用交错网格后，关于u，v的离散方程是通过对u与v各自的控制容积积分得到的。例如，式（4.9.2）的第一式是关于u的方程，对其离散时，在u控制容积中积分，即

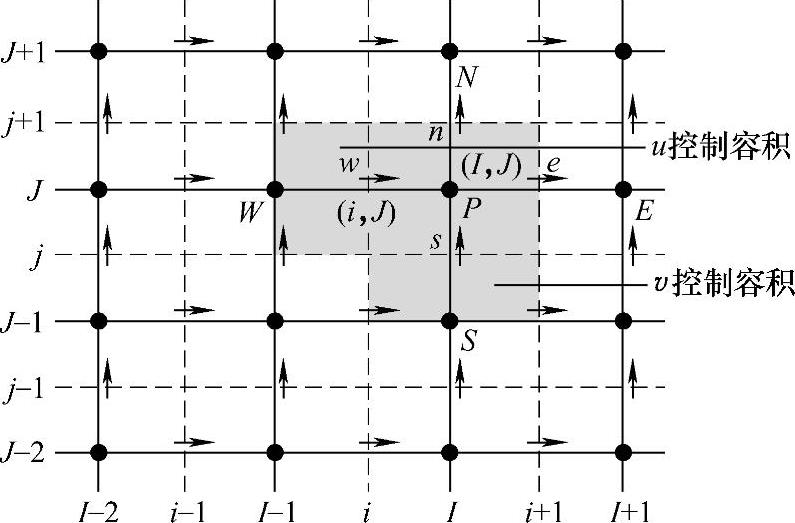
图4.9.3 速度压力控制容积与网格编号

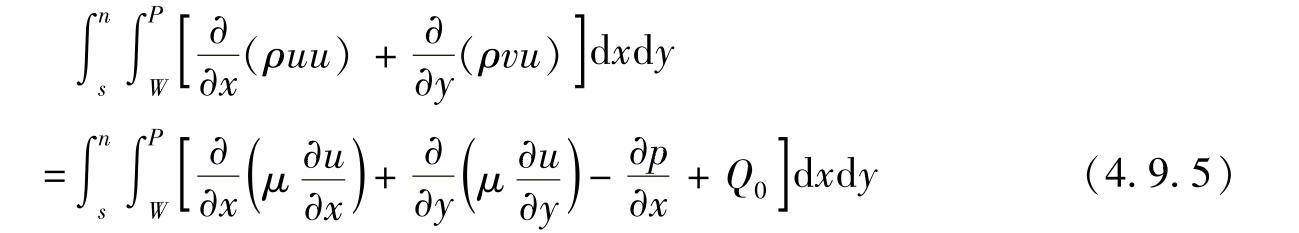
式(4.9.5)巾，关于压力梯度项的积分为

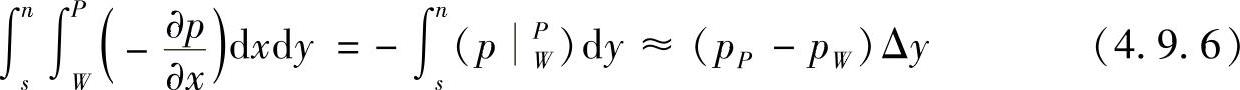
同理，可得

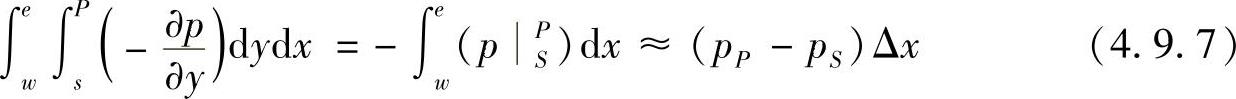
可见，直接采用相邻两结点上的压力值即可得到压力梯度项的控制容积积分结果，这样的处理方法，即使对于图4.9.1和图4.9.2所示的锯齿形压力分布也没有问题，从而解决了常规网格系统所遇到的问题。但采用交错网格也要付出代价，例如，对二维问题网格系统中有三套网格，各自的结点编号及其相互间协调问题比较复杂。图4.9.3中采用小写的（i-1），i，（i+1）等来表示x方向u网格的结点位置，采用小写的（j-1），j，（j+1）等来表示y方向v网格的结点位置，采用大写的（I-1），I，（I+1）和（J-1），J，（J+1）等来分别表示主控制容积网格x方向和y方向的结点。因此，小写的i序列和大写的J序列的组合表示u网格结点位置，如u_i，J；大写的I序列和小写的j序列的组合表示v网格的结点位置，如v_I，j，主控制容积的结点位置则采用大写的I，J序列表示，如p_I，J。此外，由于复杂的网格编号系统的寻址和插值计算也使计算工作量有所增加，尽管如此，交错网格系统还是从根本上解决了压力梯度项离散时遇到的困难，因此得到了广泛应用。

图4.9.3所示的网格错位只是一种形式，可称为向后错位。因为u网格和v网格都是相对于主控制容积的网格在各自的方向上向上、向后错了半个步长，另外一种错位形式是所谓的向前错位，即网格和v网格相对于主控制容积向前错过半个网格步长，这两种交错网格形式均可采用。

2.方程离散

动量方程式（4.9.2）中前两式的离散与前述对流扩散方程的离散并没有什么大的区别，只是多了一项压力梯度项，其离散式为式（4.9.6）和式（4.9.7）。

（1）x方向动量方程的离散

在新的网格编号条件下，x方向动量方程关于速度u在其控制容积结点位置（i，J）处的离散方程为

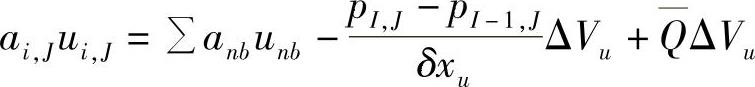
或

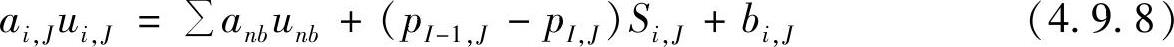
式中，ΔV_u为u控制容积体积；b_i，J=QΔV_u为u动量方程的源项；S_i，J为u控制容积东侧或西侧界面面积。从式（4.9.8）可看出，压力梯度项的计算结果是通过u控制容积边界面结点上的压力值近似计算得到的。

原符号系统下离散方程中所对应E，W，N和S的各项在新的编号系统中包含在∑a_nbu_nb中，分别对应（i+1，J），（i-1，J），（i，J+1）和（i，J-1）。各点的详细位置如图4.9.4所示。

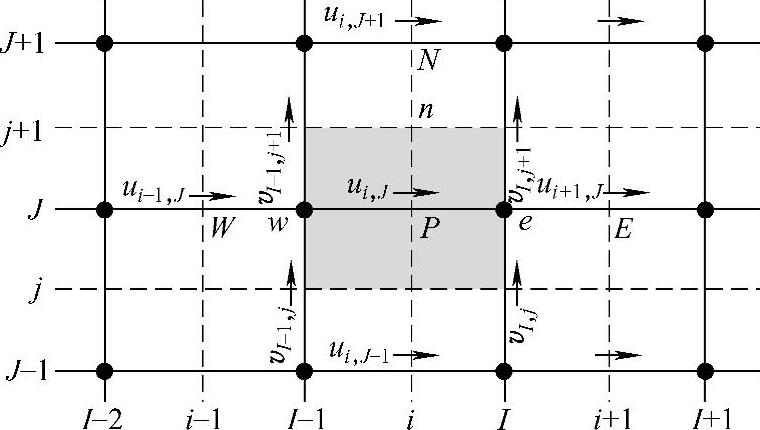
图4.9.4u 控制容积及相邻结点速度分量

式（4.9.8）中系数a_i，J和a_nb的计算与对流扩散问题离散时相同，可以采用任意一种差分格式计算，如上风差分、混合格式、乘方格式或QUICK格式。事实上，各种差分格式的离散方程系数a_i，J和a_nb都是控制容积边界单位面积对流量F（=ρu）和单位面积扩散量D（=Γ/δx）的组合。对于均匀网格，在新的网格编号系统情况下，u控制容积e，w，n和s各表面的F值与D值计算公式为(www.daowen.com)

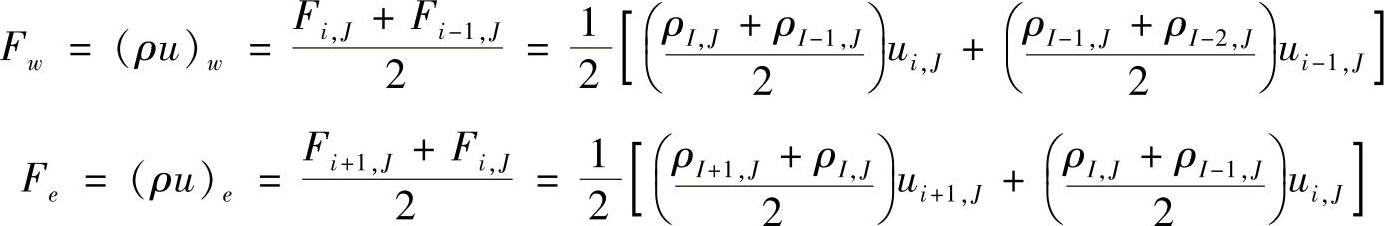
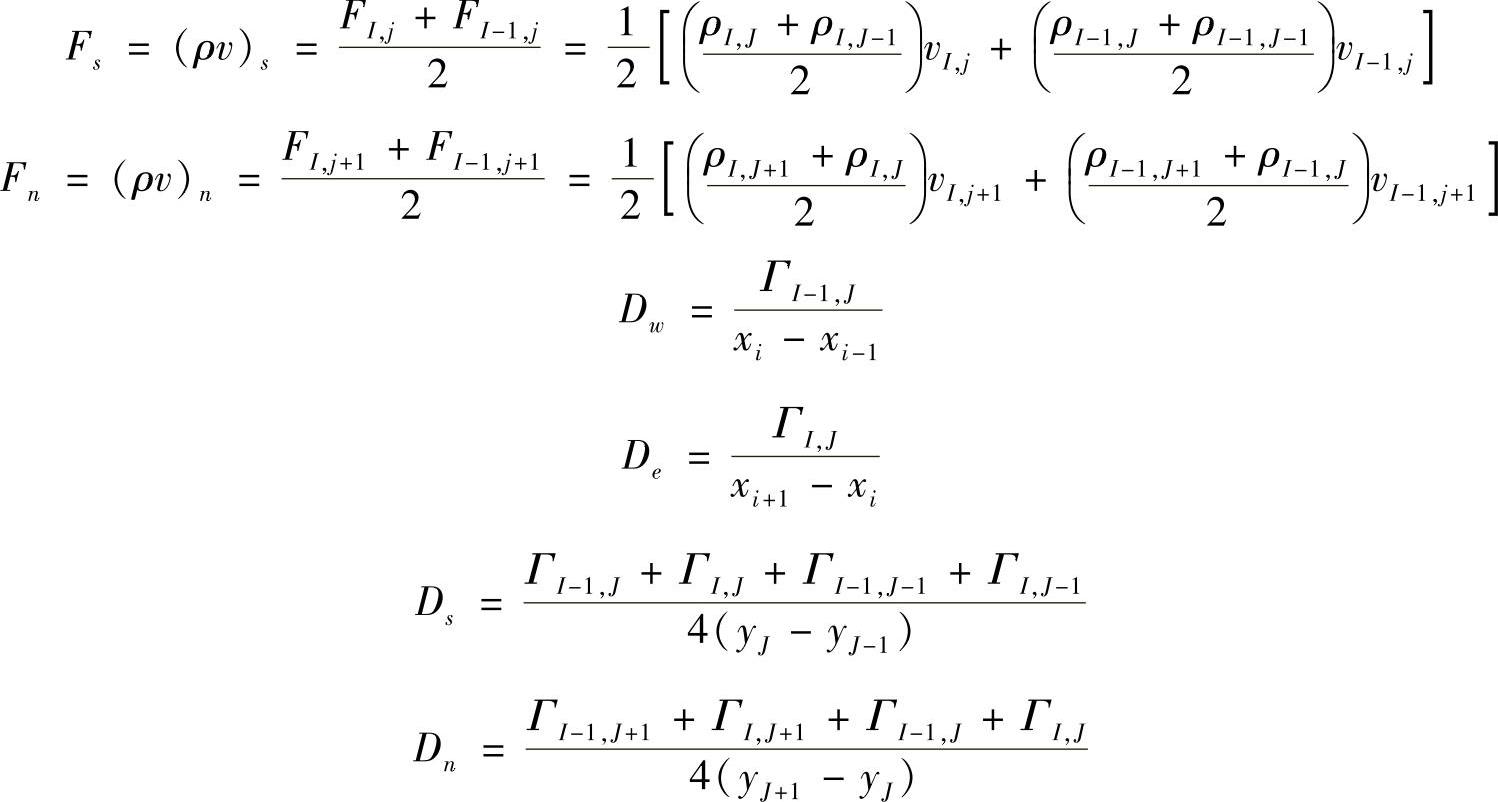
以上各式看起来较复杂，这是由于交错网格的应用引起的，所有的标量值，包括压力、密度、扩散系数等都是存储在主控制容积上的，网格中只有两个下标均为大写的结点处的标量值p，ρ，Γ认为是已知的。因此，凡涉及计算控制容积界面处ρ和Γ的位置为非主控制容积结点位置时，ρ和Γ的计算均要利用结点值进行插值计算，例如

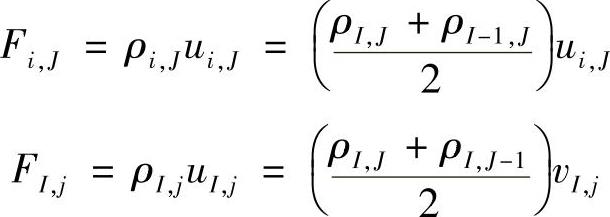
其余类似。对于D_n和D_s的计算，由于点（i，j）和（i，j+1）在x方向的两侧均无主控制容积的结点，因此还必须利用周围结点进行两次线性插值计算，如

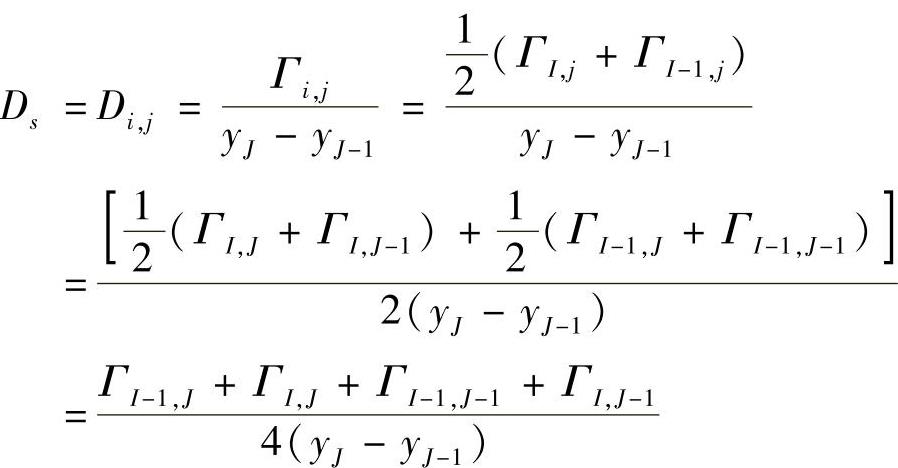
对于D_n的计算也是类似的。

应当指出，在计算各F项时所用到的速度分量u和v也认为是已知的，它们来自上一层计算的迭代结果或初始设定值，而离散方程中u_i，J和u_nb是本层迭代要求解的。

（2）y方向动量方程的离散

y方向动量方程关于速度v在其控制容积结点位置（I，j）处的离散方程为

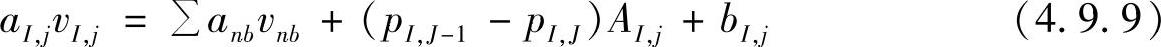
控制容积及其相邻点的速度值示于图4.9.5中，式（4.9.9）的系数a_I，j和a_nb同样是由v控制容积边界单位面积对流量F和单位面积扩散量D的组合。对于均匀网格，在新编号系统情况下，v控制容积e，w，n和s各表面的F值与D值计算公式为

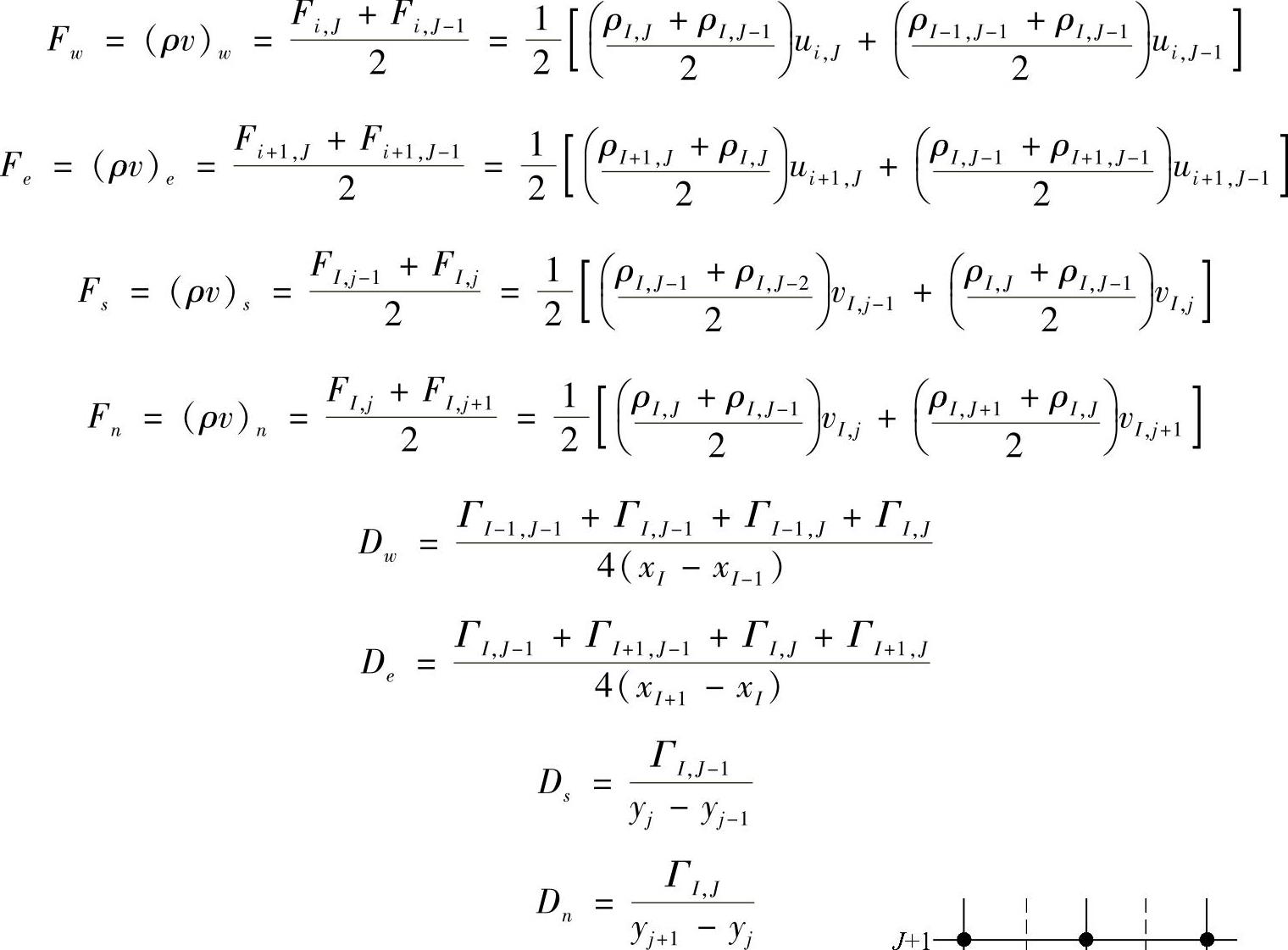
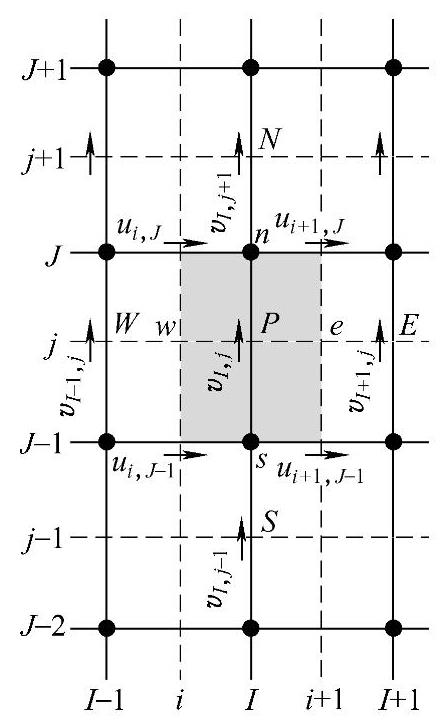
图4.9.5 v控制容积及相 邻结点速度分量

式中计算各F项时所用到的速度分量u和v认为是已知的，它们来自上一层迭代结果或初始假设值。

（3）连续性方程的离散

连续性方程是在主控制容积中积分，因此与对流扩散方程的离散格式一致。离散后的方程为

[（ρuS）_i+1，J-（ρuS）_i，J]-[（ρvS）_I，j+1-（ρvS）_I，j]=0 （4.9.10）

将式（4.9.8）、式（4.9.9）和式（4.9.10）组合，得到交错网格条件下二维压力速度耦合问题的有限体积法离散方程组，即

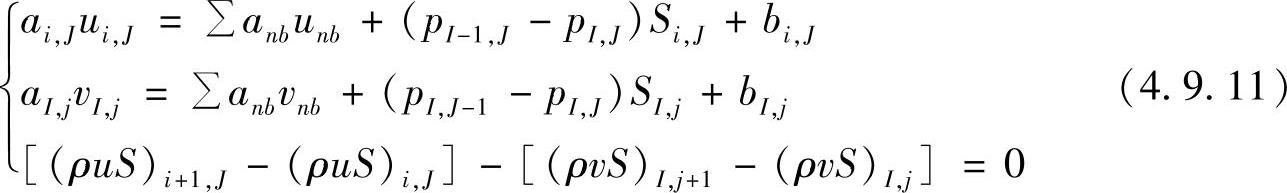
如前所述，通常采用顺序求解法解该方程组。当压力分布为已知时，可通过前两式分别求出x方向速度分布u和y方向速度分布v，如果压力分布是正确的，解出的u与v应满足连续性方程，但一般来讲，压力分布是未知的，要通过方程组（4.9.11）来确定，所以需找到求解压力p的方程，使得顺序求出的u，v，p能满足方程式（4.9.11）。