对流扩散方程中无压力梯度项，而压力梯度是引起流动的直接动力。在对流扩散问题计算中可简单理解为压力项已并入源项。而在实际流场分析中，压力场是需要求解的，且压力场与速度分布密切相关，压力与速度是耦合在一起的。一维稳态压力与速度耦合问题的控制方程为

二维稳态压力与速度耦合问题的典型方程就是不可压缩流体流动方程

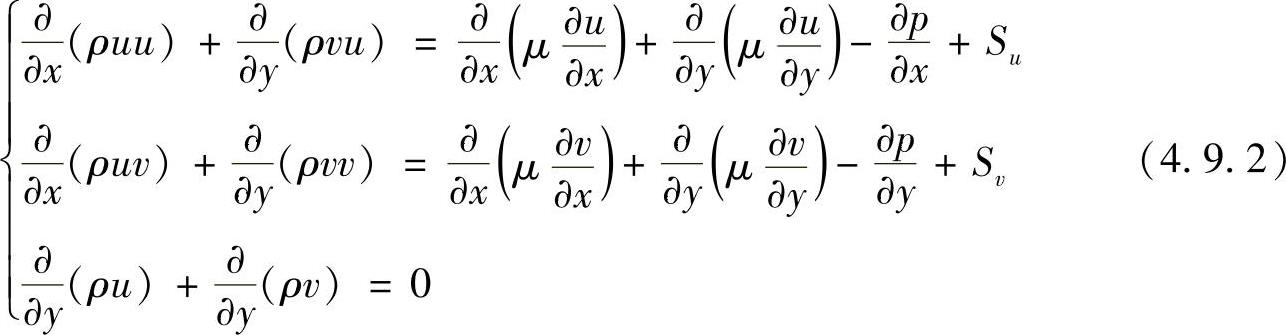
式中，前两式为x方向和y方向的动量方程，它们可看成对流扩散通用方程中场变量ϕ换成u或v，再加入压力梯度项-∂p/∂x和-∂p/∂y得到的，第三式为连续性方程。三个方程耦合，即速度场需满足连续性方程，压力场会影响速度分布。

有限体积法求解压力与速度耦合问题时，需计算控制容积界面上的压力值，这就不可避免地要采用邻近结点值来近似计算。若计算区域为均匀网格，同时压力梯度项在控制容积界面处的近似值采用中心差分格式计算，则有

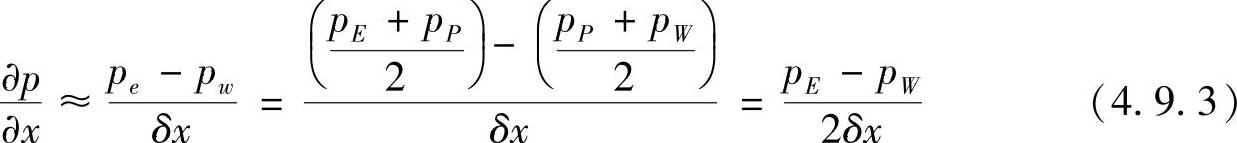
同理，对二维问题还有

(www.daowen.com)

从式（4.9.3）和式（4.9.4）可看出，结点P的压力梯度离散格式与结点P处的压力无关。

若一维问题的压力分布如图4.9.1所示，二维问题的压力分布如图4.9.2所示，则方程中∂p/∂x和∂p/∂y的计算结果处处为零，即压力场的影响在这种情况下完全被忽略，流体流动的动量源在离散方程中没有体现，甚至对于锯齿波形压力场，运动方程对这样一个波形压力场的“感受”竟然与对均匀的压力场的“感受”一样，这显然这是不正确的。

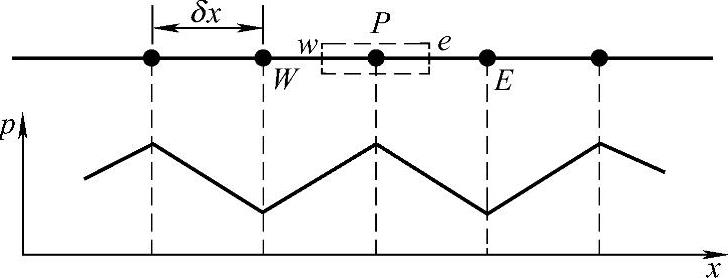
图4.9.1 一维压力分布

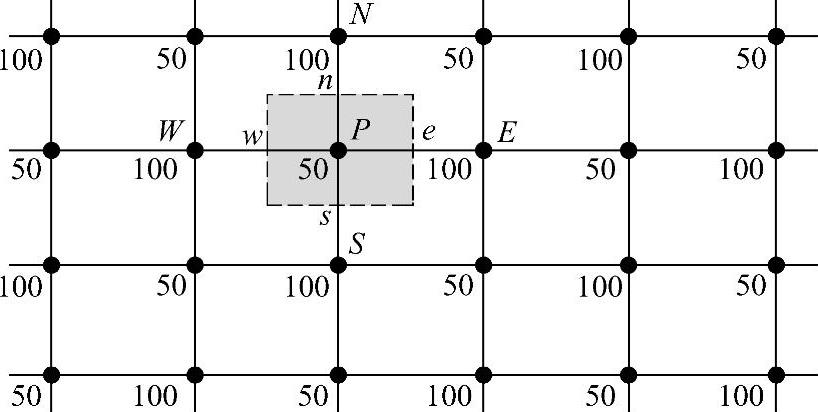
图4.9.2 二维压力分布

我们知道，式（4.9.2）称为不可压缩流体流动的NS方程，该方程是流体流动和传热计算中的重要方程。方程求解时要解出速度场u，v的分布和压力p的分布，求解此类问题大多采用顺序求解法，即对u，v，p分别独立求解。求速度场u时认为v和p的分布为已知，求速度场v时认为u和p的分布为已知，同理，求解压力场p时认为速度场u和v为已知。通常经过一次求解不能得到正确结果，需要反复迭代。由于速度场和压力场是互相耦合的，速度场的变化会影响到压力分布，压力场的变化也会反过来影响速度分布。采用顺序法求解时，应能从速度场计算结果中得到改进压力场的计算式，同理，从压力场的计算结果中也应取得改进速度场的计算式，以供下一层次迭代时引用，但这一改进式从方程组中无法直接得到。方程式（4.9.2）中没有关于描述压力p的独立方程，压力是作为动量源项出现在动量方程中的，而压力和速度的耦合关系隐含在连续性方程中，因此，压力场如何得到，如何依据当前速度场计算值来改进压力场就成为计算过程中一个很大的障碍。

对于第一个问题，即运动方程中压力梯度离散所遇到的困难，可采用交错网格技术来克服；针对第二个问题，即连续性方程离散所遇到的困难，可采用压力耦合方程的半隐计算格式（SemiImplicit Method for PressureLinked Equation），即所谓SIMPLE算法解决。