中心差分格式计算精度较高（具有二阶截差），但不具有输运特征，上风差分格式和混合差分格式具有输运特征，但计算精度较差（具有一阶截差），同时还可能引起假扩散。为了提高计算精度，在计算控制容积界面的参数值时，可考虑更多的相关结点，采用更高次的插值公式计算。

1.对流扩散问题的二阶上风差分格式——QUICK格式

所谓QUICK格式是用于计算控制容积界面值的二次插值计算格式。它是“对流项的二次上风插值”的英文缩写（Quadratic Upwind Interpolation for Convective Kinematics）。QUICK格式利用控制容积界面两侧的三个结点值进行插值计算。其中，两个结点位于界面的紧邻两侧，另一个结点位于上风侧的远邻点，如图4.8.1所示。

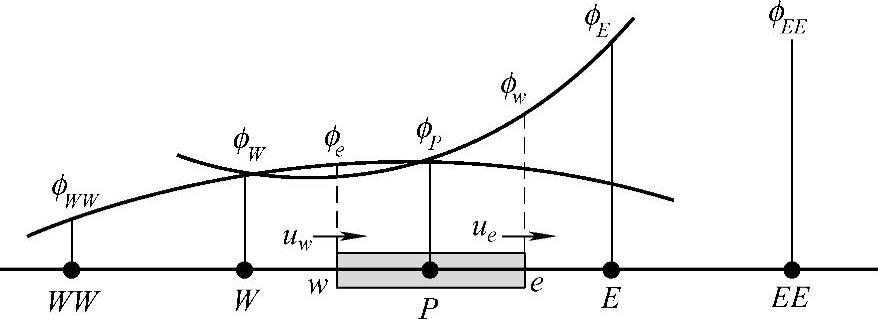
图4.8.1 QUICK格式二次插值示意图

当u_w＞0，u_e＞0时，通过结点WW，W和P的拟合曲线用于计算控制容积西侧界面参数ϕ_w，而通过结点W，P和E的拟合曲线用于计算控制容积东侧界面参数ϕ_e。若u_w＜0，u_e＜0，则结点W，P，E用于计算控制容积西侧界面参数ϕ_w，结点P，E，EE用于计算控制容积东侧界面参数ϕ_e。设表示控制容积某界面两侧的结点分别为i和（i-1），上风侧的远邻结点为i-2。则当采用均匀网格时，界面插值计算公式为

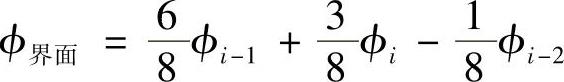
当u_w＞0时，紧邻控制容积西侧界面的两个结点为W和P，上风侧远邻点为WW，则

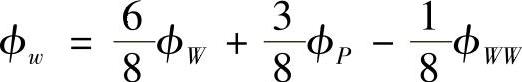
当u_e＞0时，紧邻控制容积东侧界面的两个结点为P和E，上风侧远邻点为W，则

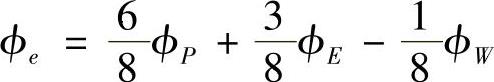
应当指出，QUICK格式中上述插值公式，仅用于计算对流项在控制容积界面处的参数值，而对于扩散项，可采用上述三点构造的拟合曲线在界面处的斜率计算，也可采用中心差分格式计算。当网格为均为网格时，两者得出相同的结果。

由一维对流扩散问题控制容积积分表达式

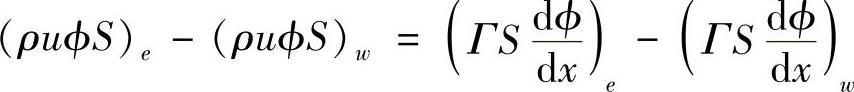
当u_w＞0，u_e＞0时，等式左侧对流项的计算根据QUICK格式，有

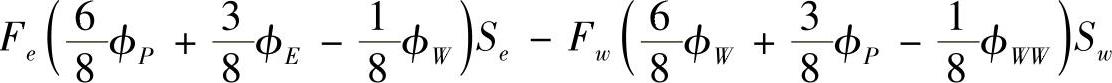
等式右侧扩散项采用中心差分格式，有

D_e（ϕ_E-ϕ_P）S_e-D_w（ϕ_P-ϕ_W）S_w

当S_e=S_w时，有

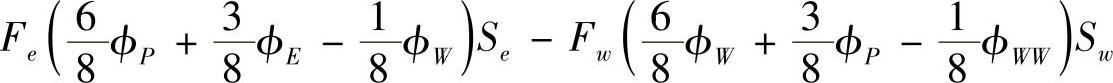
=D_e（ϕ_E-ϕ_P）-D_w（ϕ_P-ϕ_W）

按结点场变量整理可得

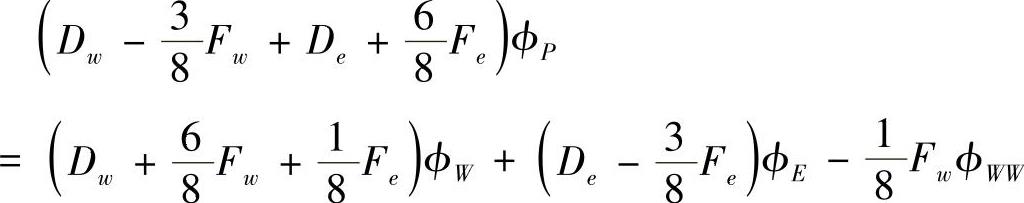
写成标准离散方程形式有

a_Pϕ_P=a_Wϕ_W+a_Eϕ_E+a_WWϕ_WW （4.8.26）

式中，

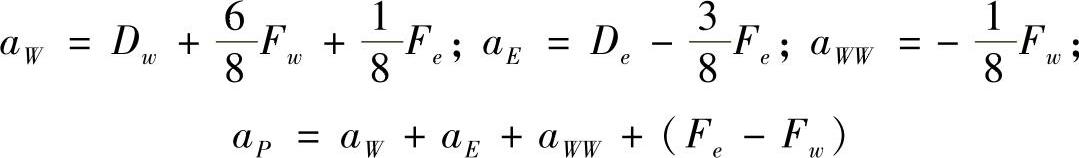
若u_w＜0，u_e＜0，则流过东侧和西侧界面的对流流量为

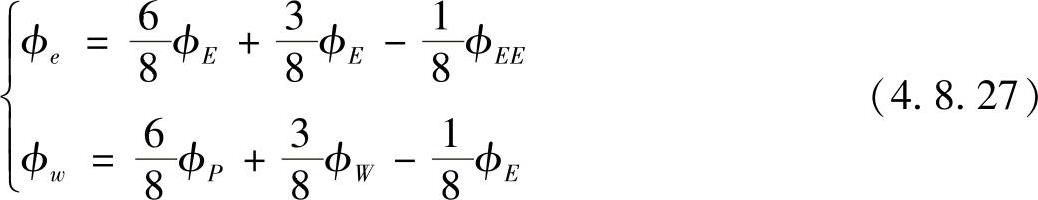
与中心差分计算的扩散项合计，可将上述各项系数改写为

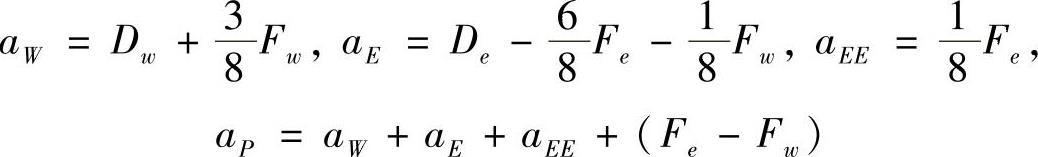
上述两个不同流动方向的计算公式可统一起来，于是，一维对流扩散问题的QUICK格式离散方程为

a_Pϕ_P=a_Wϕ_W+a_Eϕ_E+a_WWϕ_WW+a_EEϕ_EE （4.8.28）

式中，

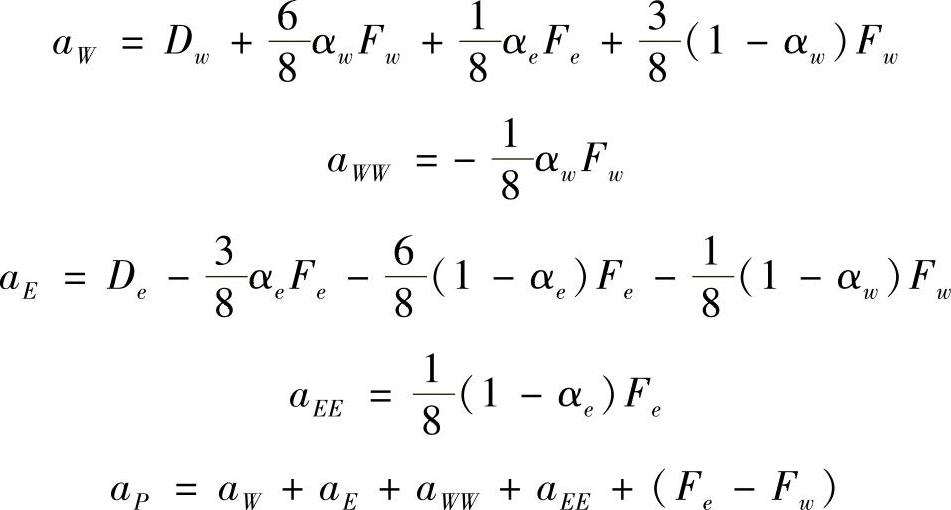
式中，当F_w＞0时，a_w=1；当F_e＞0时，α_e=1；当F_w＜0，α_w=0；当F_e＜0时，α_e=0。

【例4.8.3】利用QUICK格式，重新计算例4.5.1，取u=0.2m/s，采用5结点网格，并将QUICK格式的数值计算结果与精确解及中心差分格式数值计算结果比较。

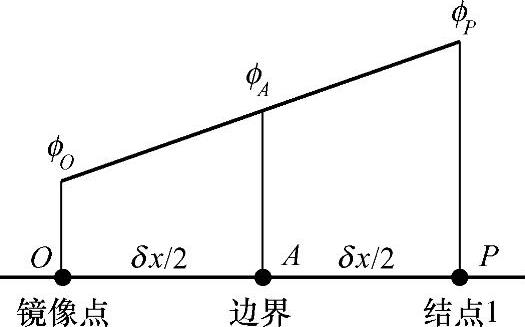
图4.8.2 边界外插构造镜像点

【解】u=0.2m/s，F=ρu=F_e=F_w=1.0×0.2=0.2，D=Γ/δx=D_e=D_w=0.5，Pe_e=Pe_w=ρuδx/Γ=0.4。内结点3和结点4的离散方程由式（4.8.28）列出，边界结点1、结点2和结点5需特殊处理，除结点1、结点5外，结点2的离散方程系数还涉及边界条件。

在结点1处，控制容积西侧界面的ϕ值由边界值ϕ_A给出，即ϕ_w=ϕ_A，但计算控制容积东侧界面值ϕ_e要用到西侧结点值ϕ_W，而此边界控制容积没有西侧结点，因此无法计算东侧界面值。解决这个问题的办法是采用线性外插，在距外边界δx/2处构造一个外部镜像点O，如图4.8.2所示。外插计算的ϕ_O满足

ϕ_O+ϕ_P=2ϕ_A

或

ϕ_O=2ϕ_A-ϕ_P

将求得的ϕ_O作为计算边界控制容积东侧界面值ϕ_e所用的西侧结点值，于是

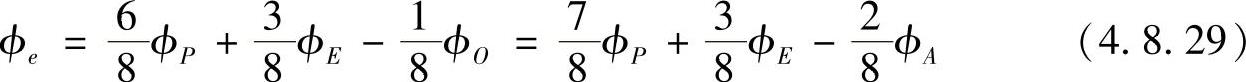
结点P，E与镜像点O构造的拟合曲线在边界处的斜率为

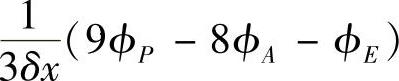
因此，控制容积西侧界面的扩散流量为

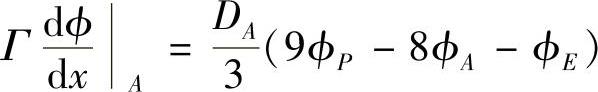
从而结点1的离散方程为

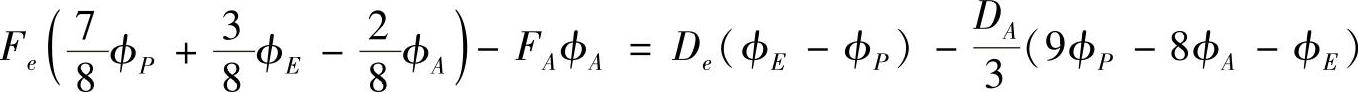
结点5所在的控制容积，东侧界面ϕ值已知，ϕ_e=ϕ_B。通过东侧界面的扩散流量比照结点1可写为(www.daowen.com)

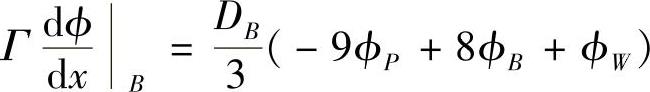
于是得到，结点5的离散方程为

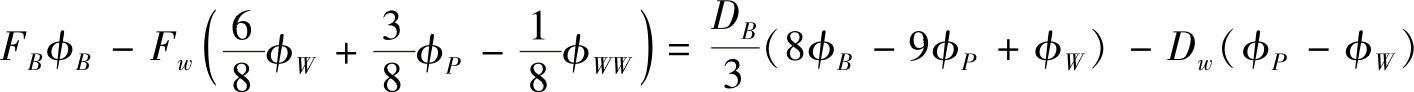
结点2的离散方程本来是可以采用内结点通用式计算的，但由于计算结点1的控制容积东侧界面对流量时采用了式（4.8.29）的特殊公式，因此在计算结点2的控制容积西侧界面对流量时也必须采用该特殊公式，以保证流动计算的协调性，故得结点2的离散方程为

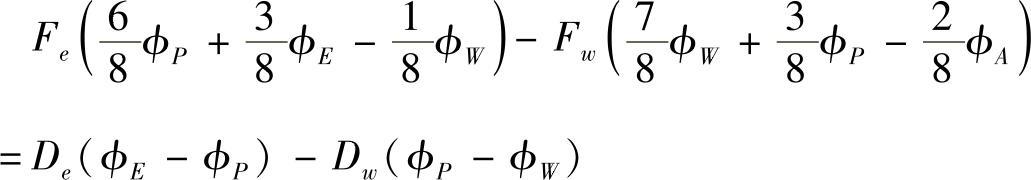
将结点1、结点5和结点2的离散方程写成统一格式，有

a_Pϕ_P=a_Wϕ_W+a_Eϕ_E+a_WWϕ_WW+Q₀

结点各系数的计算公式见表4.8.11。

表4.8.11 离散方程系数

将已知数值代入可得离散方程各系数值，见表4.8.12。

表4.8.12 离散方程系数

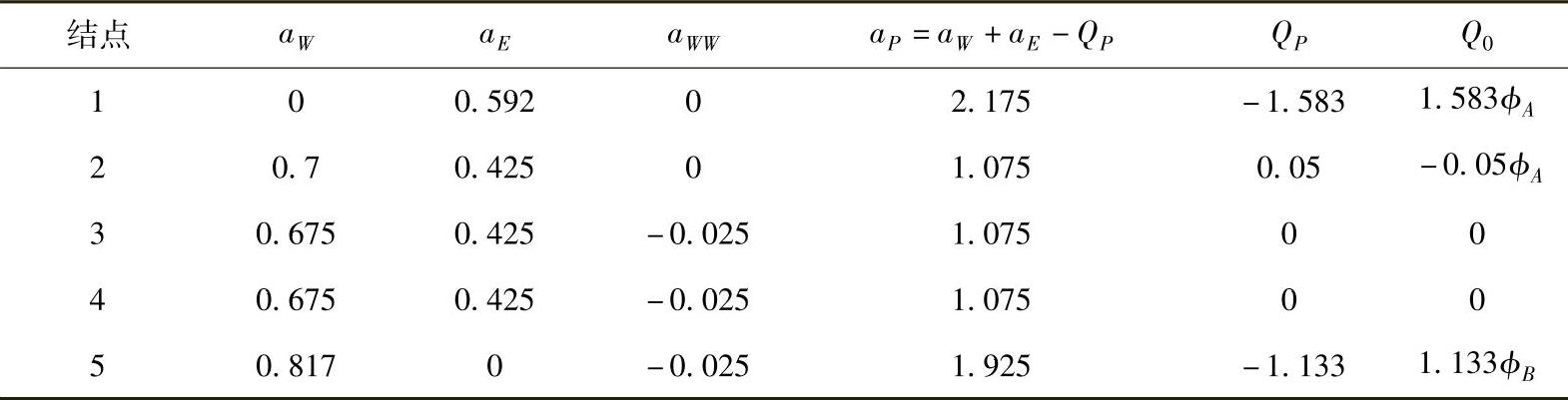
将ϕ_A=1，ϕ_B=0代入，解离散方程，可得

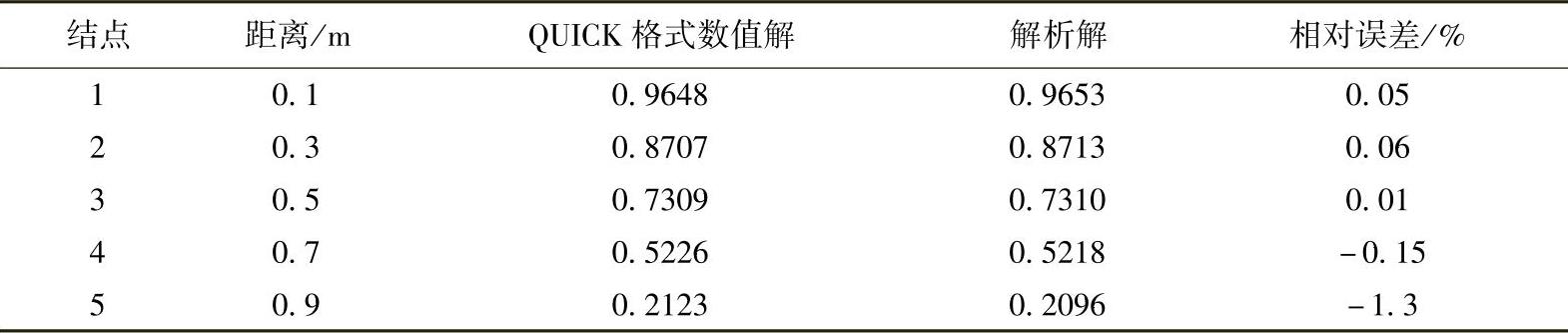
解析解与数值解的计算结果比较列于表4.8.13。可见，采用QUICK格式计算的数值解与解析解结果吻合地很好，且优于中心差分格式的计算结果。

2.QUICK格式的特征

（1）守恒性

表4.8.13 解析解与QUICK格式数值解对比

QUICK格式在计算相邻控制容积公共界面处的参数值时，采用不同的三结点插值，从图4.8.1看起来似乎不能实现公共界面上通量守恒。事实上，QUICK格式是分段线性插值，同时在界面参数值计算时引入修正率来修正公共界面处的插值曲线斜率。例如，对控制容积东侧界面上场变量ϕ_e的计算公式为

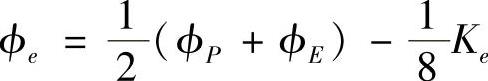
式中，K_e为修正率，

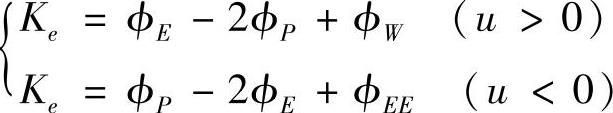
同理，对于西侧界面上场变量值ϕ_W的计算公式为

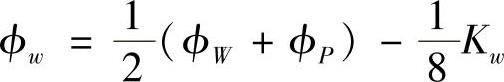
式中

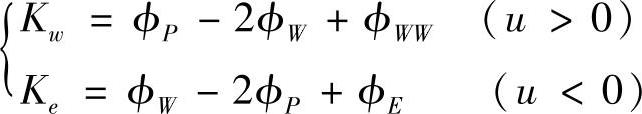
如图4.8.3所示，结点i代表的控制容积东侧界面e_i与结点i+1所代表的控制容积西侧界面w_i+1为公共界面。当u＞0时，场变量ϕ在e_i处的对流量按QUICK格式计算公式为

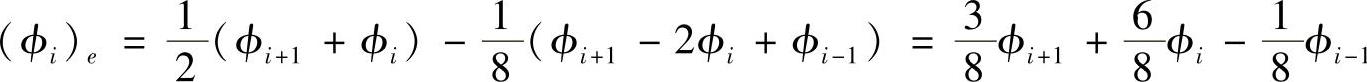
可见，ϕ_i在e_i处的流量正好等于ϕ_i+1在w_i+1处的对流流量，即（ϕ_i）_e=（ϕ_i+1）_w。

当u＜0时，有

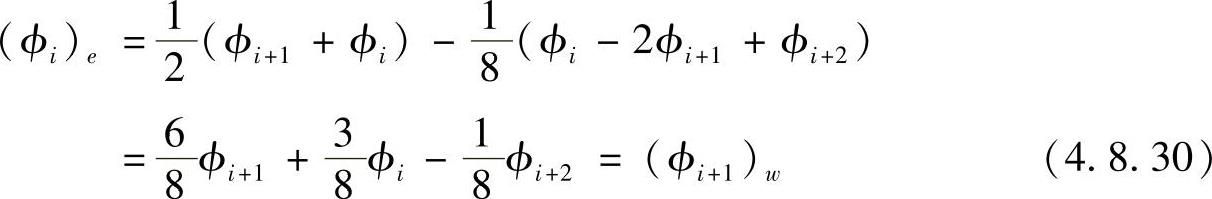
同样等于ϕ在w_i+1处的对流量。

对于扩散项的计算，或采用中心差分，或采用界面处公共斜率计算也可保证守恒性要求，因此QUICK格式是守恒的。

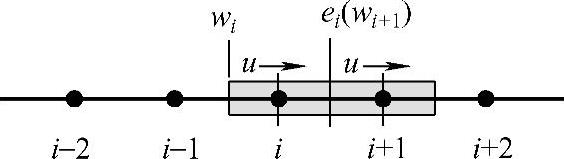
图4.8.3 QUICK格式守恒性

（2）有界性

QUICK格式不能保证a_W和a_E恒为正数，且a_WW和a_EE总是为负值，因此QUICK格式不能恒满足有界性要求。可以证明，当网格数Pe＞8/3时，可能会出现解的不稳定现象。所以说QUICK格式是条件稳定的，计算结果有可能出现振荡。

（3）输运性

QUICK格式计算控制容积界面参数值总是采用上风2个结点和下风1个结点进行插值，计算格式可以反映输运特征。此外，由于QUICK格式计算控制容积界面参数值采用3个结点插值，计算结果具有三阶截差，精度较高，假扩散很小，若能保证网格数Pe＜8/3，计算结果具有很高的计算精度。

3.QUICK格式的修正

QUICK格式计算精度高，在流动和传热的数值计算中得到了广泛应用，但这种格式除了不满足有界性要求外，还有两个缺点限制了它的应用。其一是差分计算要用到3个结点，计算边界结点离散方程时无上风侧远邻结点可供利用，对此，可采用例4.8.3中的方法解决这个问题，还可以采用一阶上风差分或混合格式等一阶差分格式来处理。第二个缺点是一维QUICK格式对控制容积积分计算要用到5个结点，二维问题涉及9个结点，与一阶差分中的一维问题三点格式，二维问题五点格式不同，求解线性代数方程组效率较低。

针对以上QUICK格式的缺陷，出现了改进的QUICK格式，其基本思想是将QUICK格式离散方程中的各项重新组合，使方程的主要系数a_W，a_E和a_P满足有界性要求，而将其余部分归入源项，同时使离散方程具有三对角特征。改进的QUICK格式为

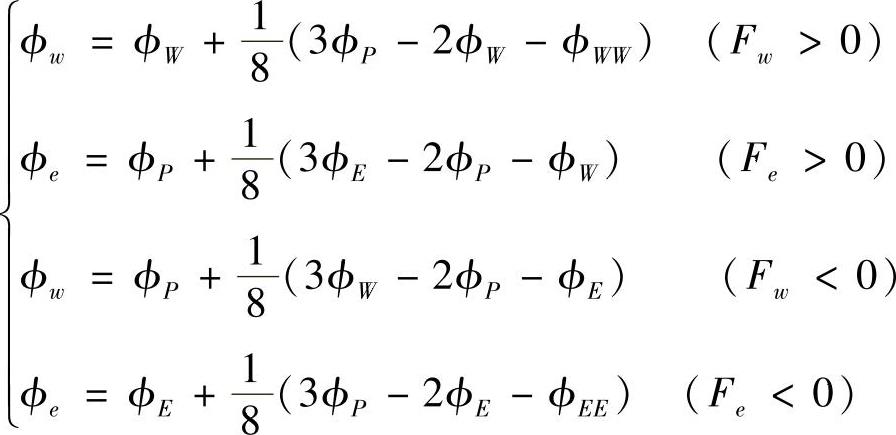
离散方程格式为

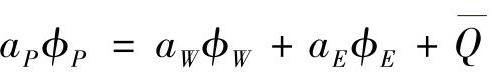
式中，

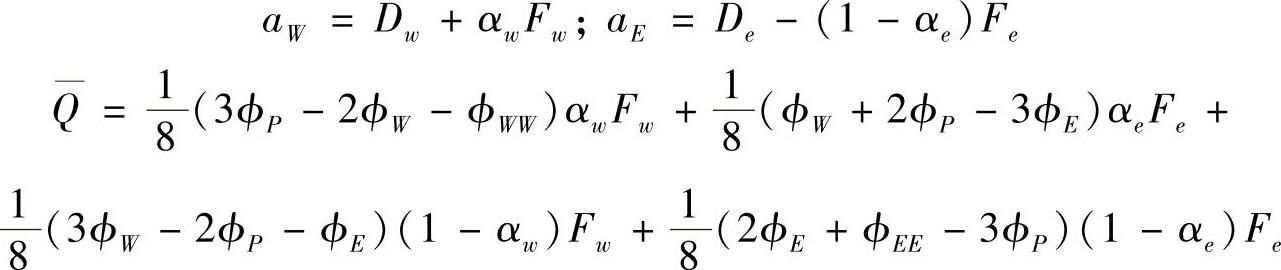
a_P=a_W+a_E+（F_e-F_w）

当F_w＞0时，α_w=1；当F_e＞0时，α_e=1；当F_w＜0时，α_w=0；当F_e＜0时，α_e=0。

改进的QUICK格式使离散方程系数为正值，满足守恒性、有界性和输运性，同时又有较高的计算精度。