1.一维混合差分格式

针对上风差分格式易出现的假扩散问题，提出了一种混合差分格式，综合了中心差分和上风差分的优点。当网格Pe数小于2时，采用中心差分格式计算控制容积界面值，它具有二阶精度，当Pe数大于或等于2时，采用上风差分格式计算控制容积界面对流输运量，同时忽略扩散输运量，尽管计算精度只有一阶，但却可以较好地反映流动的输运特征。

混合差分格式采用网格Pe数作为计算控制容积界面值方法的判据。例如，点P控制容积西侧界面的网格Pe数为

则对于无源稳态对流扩散问题的混合差分格式的近似式中，通过西侧界面的场变量ϕ的净流量为

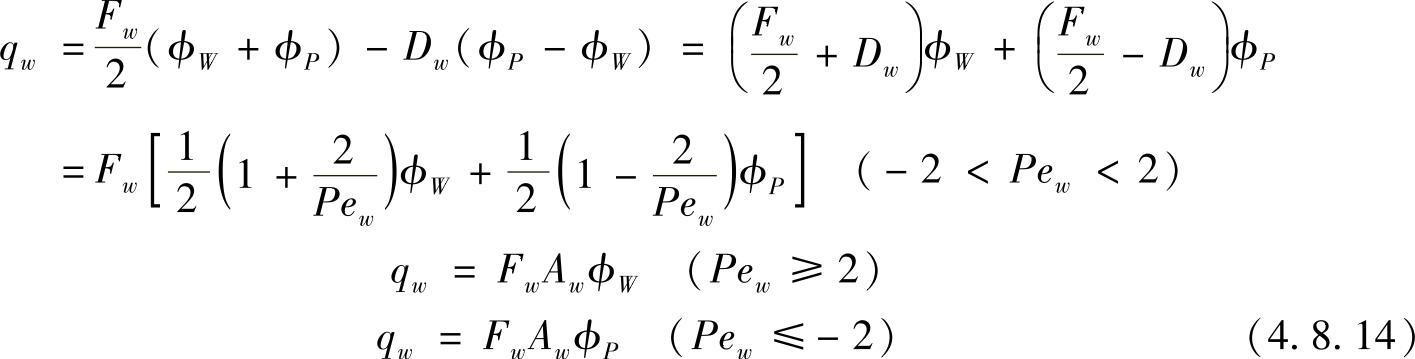
从式（4.8.14）可看出，当网格Pe数较小时（Pe＜2），对流项和扩散项的近似计算均采用中心差分，而当Pe≥2时，对流项近似计算采用上风差分，同时对扩散项置零，也就是说当Pe≥2时，消除了扩散项的影响，可避免出现假扩散现象。

混合格式条件下对流扩散问题的离散方程通用形式为

a_Pϕ_P=a_Wϕ_W+a_Eϕ_E （4.8.15）

式中，

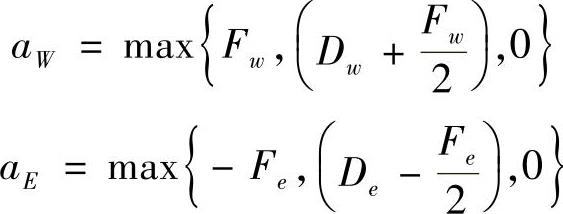
a_P=a_W+a_E+（F_e-F_w）

【例4.8.2】利用混合差分格式计算例4.5.1中的第二种工况。

【解】采用5结点网格时，δx=0.2m，u=2.5m/s，则F_e=F_w=F=ρu=2.5，D_e=D_w=D=Γ/δx=0.1/0.2=0.5，Pe_e=Pe_w=ρuδx/Γ=5。可见网格Pe数大于2，因此，混合差分格式计算界面对流流量时采用上风差分，不考虑扩散项的影响。

利用式（4.8.15）可求出内结点2，3和结点4的离散方程系数，对边界结点则需特殊处理。

在边界结点1，由混合差分格式近似计算，有

F_eϕ_P -F_Aϕ_A=0-D_A（ϕ_P-ϕ_A）

在边界结点5，有

F_Bϕ_P -F_wϕ_W=D_B（ϕ_B-ϕ_P）-0

也就是说，只考虑边界的扩散流量，对流仍按上风差分格式计算。

因F_A=F_B=F，D_A=D_B=2Γ/δx=2D，可统一列出离散方程系数，由表4.8.7给出。(www.daowen.com)

表4.8.7 离散方程系数

将已知数据代入，可得到离散化方程的系数，见表4.8.8。

表4.8.8 离散化方程系数

解离散方程可得

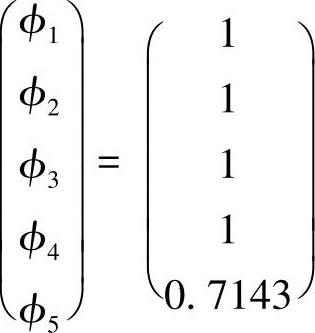
混合差分格式数值解与解析解的计算结果比较列于表4.8.9中。

表4.8.9 解析解与混合差分格式数值解对比

可见，这个计算结果与解析解相差太大，不可接受。若将求解区域离散成较密集的网格系统，可以预期得到较精确的计算结果。

2.高维混合差分格式

混合差分格式可推广到二维和三维情况。离散方程的通用格式仍为

a_Pϕ_P=a_Wϕ_W+a_Eϕ_E+a_Sϕ_S+a_Nϕ_N+a_Bϕ_B+a_Tϕ_T+Q₀

a_P=a_W+a_E+a_S+a_N+a_B+a_T+ΔF-Q_P

方程中各系数计算式列于表4.8.10。

表4.8.10 混合差分格式离散方程系数

混合差分格式取中心差分和上风差分的优点，部分克服了它们的缺点。当Pe数较小时，采用中心差分，计算结果有较高的精度；当Pe数较大时，采用上风差分计算对流项在控制容积界面处的近似值，而将扩散流量置零，这样可减弱假扩散的影响。从中心差分和上风差分特性的讨论中可知，混合差分格式满足守恒性的要求。从表4.8.10中可看出，离散方程系数永远保持正值，可满足有界性的要求。Pe数较大时的上风差分计算保证了输运特性，混合差分格式被广泛用于解决流动与传热问题。混合差分格式的缺点是Pe＞2时计算结果只有一阶精度，为提高计算精度必须采用较密集的网格系统。