二维对流扩散问题控制微分方程的一般形式为

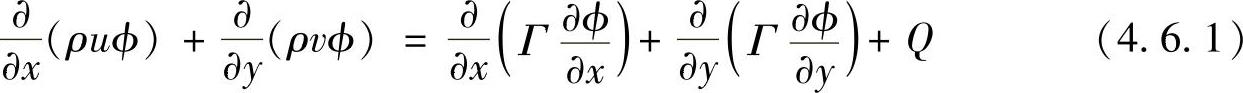
式中，u为场变量ϕ在x方向的流速；v为ϕ在y方向的流速，在推导过程中均认为是已知值；Γ为ϕ的扩散率；Q为源项。

仍采用图4.4.1所示离散网格，对方程式（4.6.1）在图4.6.1所示的控制容积内积分，有

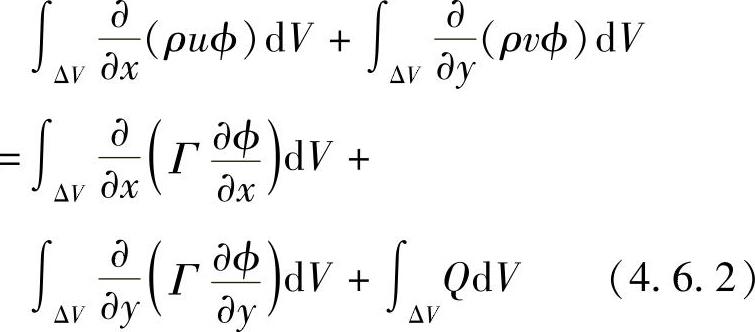
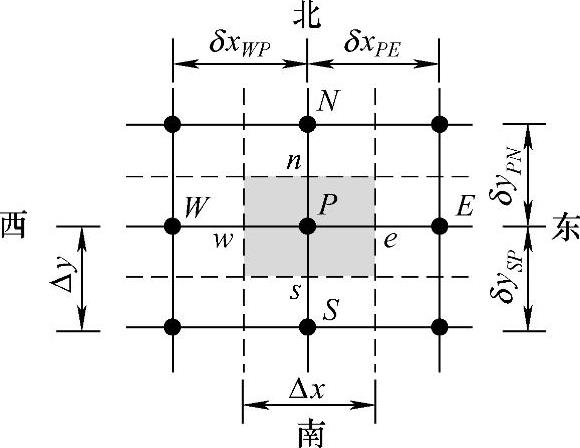
图4.6.1 网格划分

从图4.6.1可知，控制容积的边界面积（长度）为

S_w=S_e=Δy，S_n=S_s=Δx

由高斯公式，方程（4.6.2）可写成

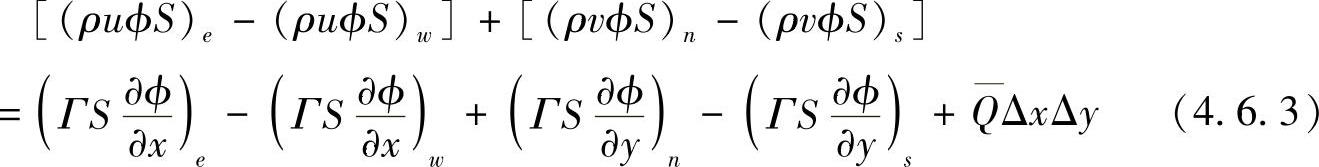
我们仍采用前面讨论的近似方法计算通过控制容积界面的场变量值或其导数值。

穿过东侧边界的对流量为

C_e=（ρu）_eS_eϕ_e=（ρu）_eS_e（ϕ_E+ϕ_P）/2

穿过东侧边界的扩散量为

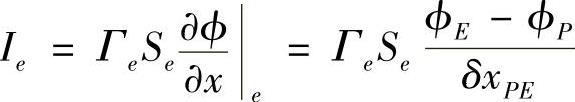
穿过西侧边界的对流量为

C_w=（ρu）wS_wϕ_w=（ρu）wS_w（ϕ_P+ϕ_W）/2

穿过西侧边界的扩散量为

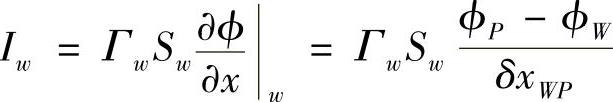
穿过北侧边界的对流量为

C_n=（ρv）n^Snϕ_n=（ρv）n^Sn（ϕ_N+ϕ_P）/2(www.daowen.com)

穿过北侧边界的扩散量为

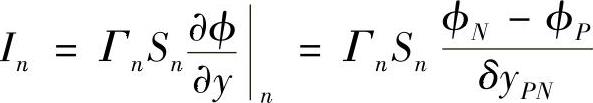
穿过南侧边界的对流量为

C_s=（ρv）_sS_sϕ_s=（ρv）_sS_s（ϕ_P+ϕ_S）/2

穿过南侧边界的扩散量为

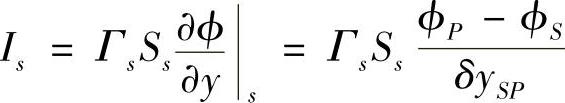
源项为

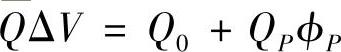
与一维对流扩散问题格式推导类似，令F=ρuS（或F=ρvS），D=ΓS/δx（或D=ΓS/δy），则有

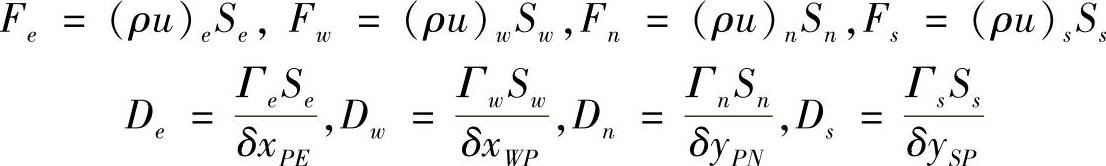
将以上各式代入式（4.6.3），有

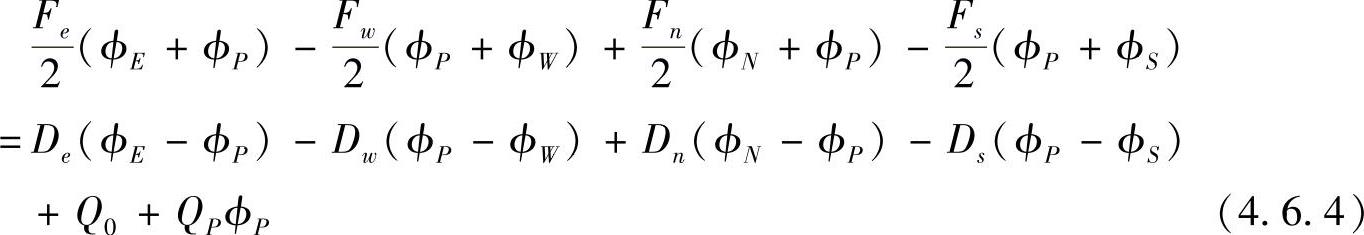
按结点场变量整理，有

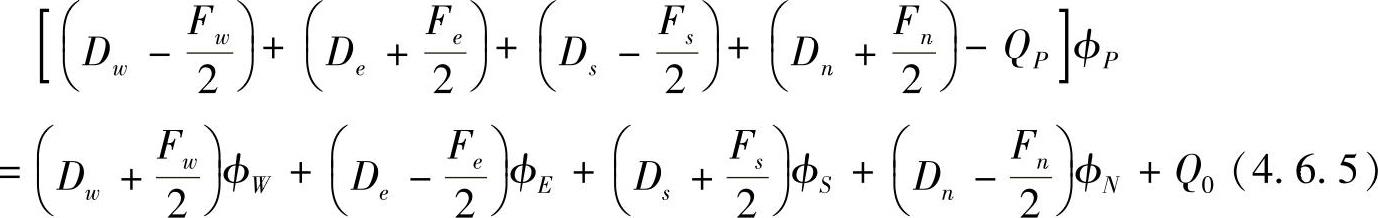
在ϕ_P的系数中加入F_e-F_e+F_w-F_w+F_s-F_s+F_n-F_n，得

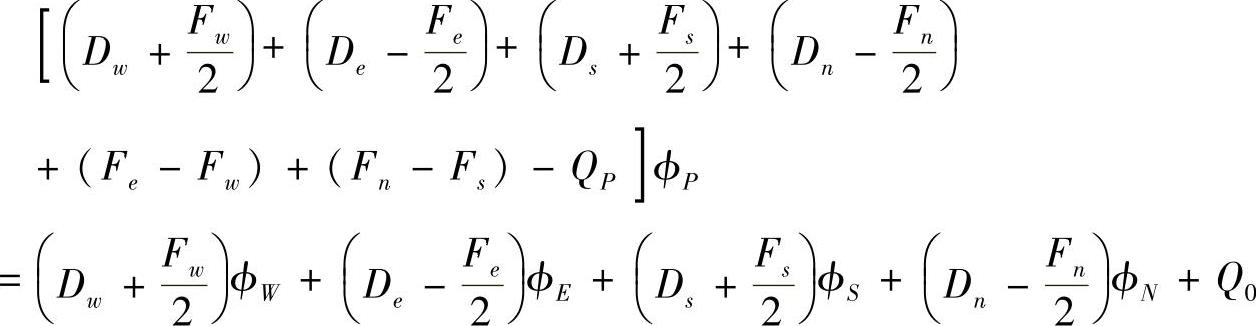
即

a_Pϕ_P=a_Wϕ_W+a_Eϕ_E+a_Sϕ_S+a_Nϕ_N+Q₀ （4.6.6）

式中，

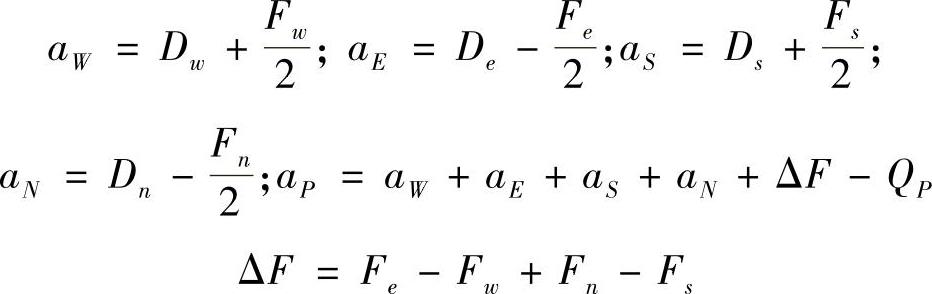
式（4.6.6）适合于所有内部结点的离散方程构造。引入边界条件后即可构成整个对流扩散问题的离散方程组，它仍然是一组代数方程组，求解该代数方程组，即可得到各结点的场变量值。