› 理论教育 ›一维对流扩散问题的有限体积法

一维对流扩散问题的有限体积法

时间：2023-10-26 理论教育 版权反馈
【摘要】：无源一维稳态对流扩散问题的场变量满足式中，ρ为流体密度；u为在x方向的流动速度。表4.5.3 解析解与有限体积法数值解对比数值计算结果接近精确解，尽管计算网格比较粗糙，但仍得到合理结果。表4.5.6 离散方程系数数值解与分析解的计算结果示于图4.5.4中，从图中可看出两者吻合得良好。

一维对流扩散问题的有限体积法

无源一维稳态对流扩散问题的场变量ϕ满足

978-7-111-44528-9-Chapter04-144.jpg

式中，ρ为流体密度；u为ϕ在x方向的流动速度。该流动还必须满足连续性方程

978-7-111-44528-9-Chapter04-145.jpg

对控制容积（见图4.5.1）积分，有

978-7-111-44528-9-Chapter04-146.jpg

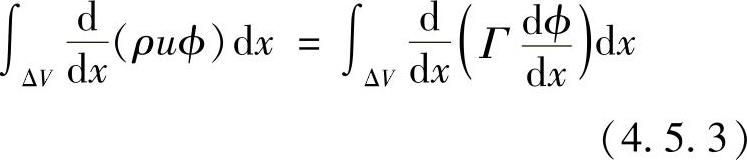
同理

978-7-111-44528-9-Chapter04-147.jpg

978-7-111-44528-9-Chapter04-148.jpg

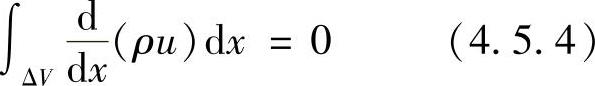
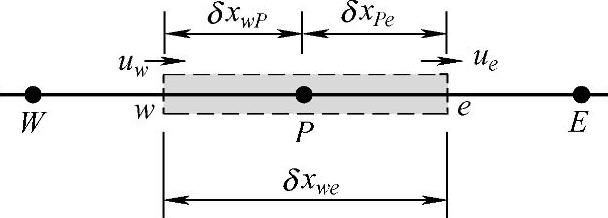
图4.5.1 控制容积及其相邻结点

由高斯公式，控制容积内对流扩散方程式（4.5.3）可写成

978-7-111-44528-9-Chapter04-149.jpg

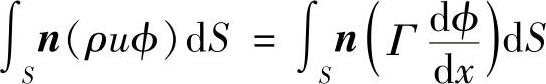
式中，S为控制容积边界面积。于是

978-7-111-44528-9-Chapter04-150.jpg

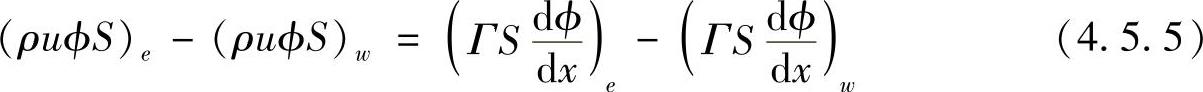
类似地，连续性方程可写为

978-7-111-44528-9-Chapter04-151.jpg

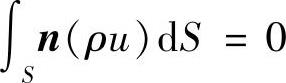
即

（ρuS）e-（ρuS）w=0 （4.5.6）

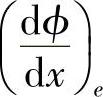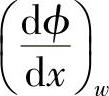与扩散问题一样，这里仍要用到控制容积边界处的值Γe，Γw，ϕe，ϕw，978-7-111-44528-9-Chapter04-152.jpg和978-7-111-44528-9-Chapter04-153.jpg，与扩散问题离散方程的推导方法相似，近似取

978-7-111-44528-9-Chapter04-154.jpg

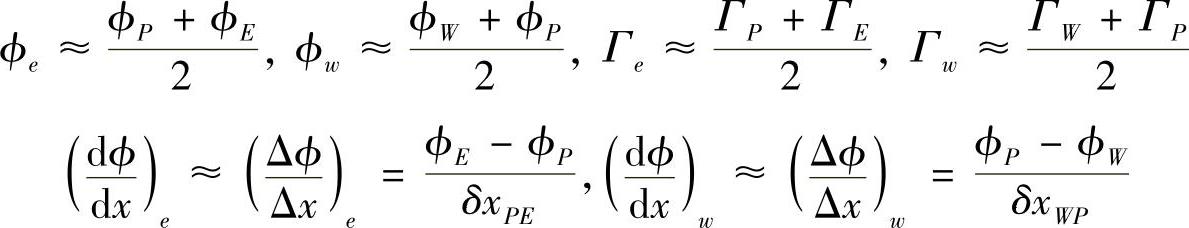
为表达简便，定义两个参数，令F=ρu表示通过单位控制容积界面的对流流量，令D=Γ/δx表示单位界面上扩散阻力的倒数。于是，有

978-7-111-44528-9-Chapter04-155.jpg

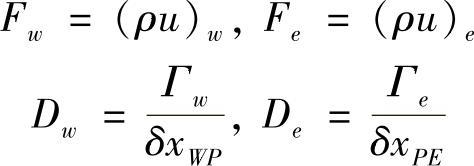
设Sw=Se=S，将以上各式代入式（4.5.5）和式（4.5.6）中，有

978-7-111-44528-9-Chapter04-156.jpg

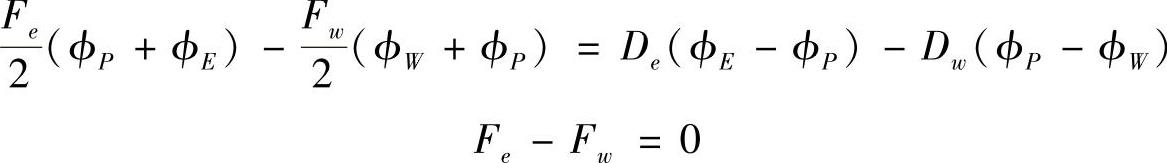
按结点场变量整理，有

978-7-111-44528-9-Chapter04-157.jpg

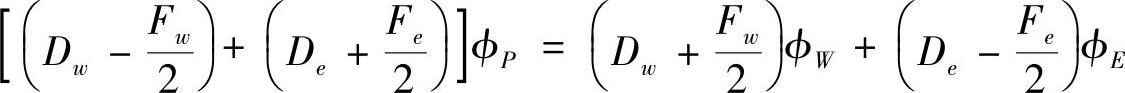
或

978-7-111-44528-9-Chapter04-158.jpg

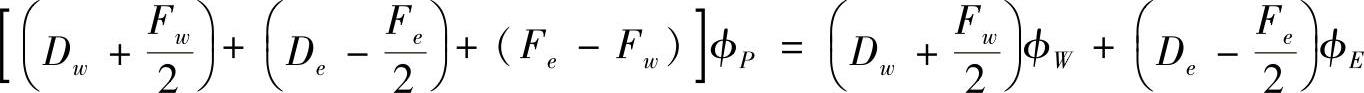
这样，我们就用结点参数值表示出了对流扩散问题的离散方程，它与扩散问题离散方程具有相同的形式

aPϕP=aWϕW+aEϕE （4.5.7）

式中，

978-7-111-44528-9-Chapter04-159.jpg

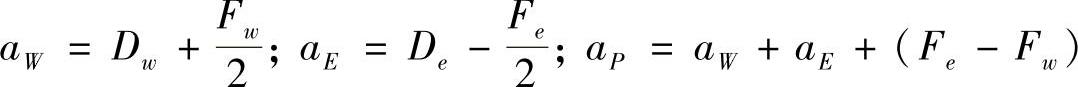
在离散区域内的所有内点均可利用式（4.5.7）写出对流扩散问题的离散方程，并将生成与扩散问题离散方程同样形式的三对角方程组，引入边界条件并求解，即得各结点处的场变量ϕ值。下面通过例题说明方程组的建立，边界条件的引入以及方程求解过程。

【例4.5.1】设某场变量ϕ经对流扩散过程从一维区域的点x=0处输运到点x=L处，如图4.5.2所示。输运控制方程为

978-7-111-44528-9-Chapter04-160.jpg

978-7-111-44528-9-Chapter04-161.jpg

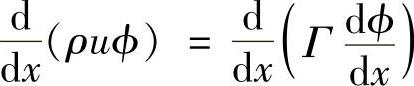
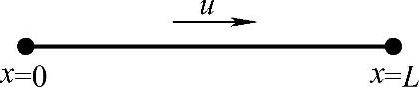
图4.5.2 算例4.5.1

流体密度ρ=1kg/m3，L=1m，扩散系数Γ=0.1kg/（m·s）。

已知此问题的理论解为

978-7-111-44528-9-Chapter04-162.jpg

试求：（1）当流速为u=0.1m/s，离散成5个结点网格时，ϕ在区域内的分布；（2）当流速为u=2.5m/s，离散成5个结点网格时，ϕ在区域内的分布；（3）当流速为u=2.5m/s，离散成20个结点网格时，ϕ在区域内的分布。

【解】求解域的离散网格如图4.5.3所示。每一个控制容积长度δx=0.2m，此时F=ρu，D=Γ/δx，Fe=Fw=F，De=Dw=D对所有控制容积成立。中间结点2，3和结点4的离散方程与式（4.5.7）一致，边界结点1和结点5需特殊处理。

978-7-111-44528-9-Chapter04-163.jpg

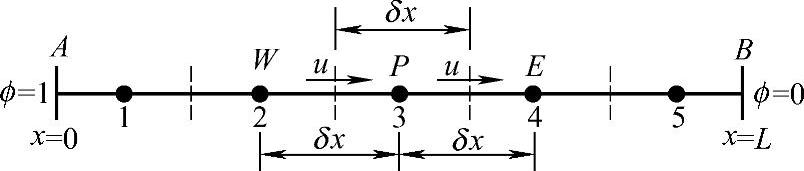
图4.5.3 网格划分

对结点1所在控制容积积分，有

978-7-111-44528-9-Chapter04-164.jpg

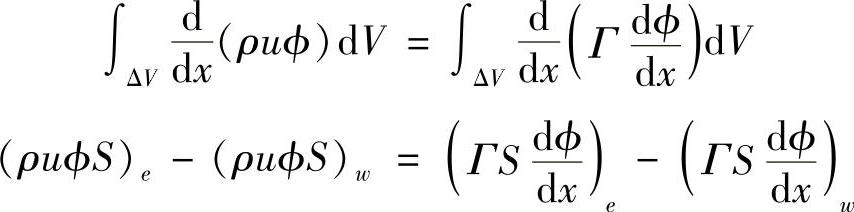
对于控制体西侧界面

978-7-111-44528-9-Chapter04-165.jpg

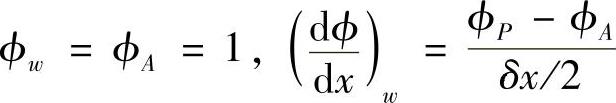
则

978-7-111-44528-9-Chapter04-166.jpg

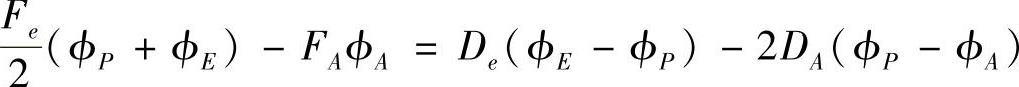
按结点场变量整理，有

978-7-111-44528-9-Chapter04-167.jpg

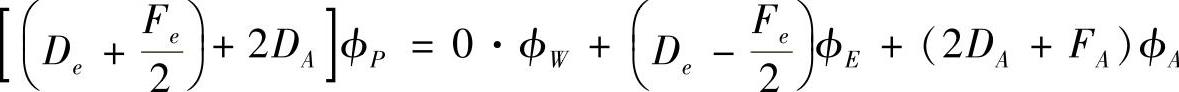
即

aPϕP=0·ϕW+aEϕE+Q0(www.daowen.com)

式中，

aW=0；aE=De-Fe/2；aP=aW+aE+（Fe-Fw）-QP；

QP=-（2DA+Fw）；Q0=（2DA+FA）ϕA

当ρu=常数时，aP表达式中

Fe -Fw=0

同理，对结点5所在的控制容积积分，可得

978-7-111-44528-9-Chapter04-168.jpg

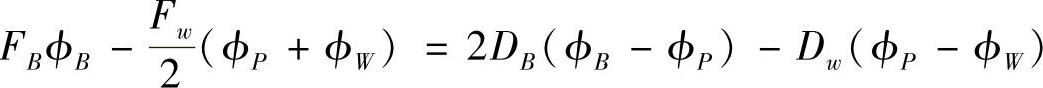
按结点场变量整理，有

978-7-111-44528-9-Chapter04-169.jpg

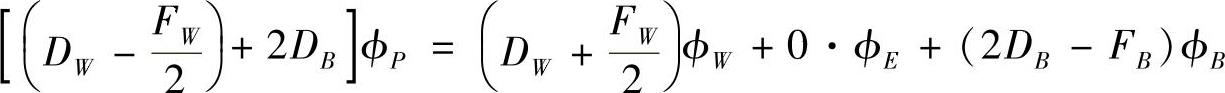
即

aPϕP=aW×ϕW+0·ϕE+Q0

式中，

aW=D+F/2；aE=0；aP=aW+aE+（Fe-Fw）-QP；

QP=-（2DB-Fe），Q0=（2DB-FB）ϕB

FW=Fe=FA=FB=F，DW=De=DA=DB=D

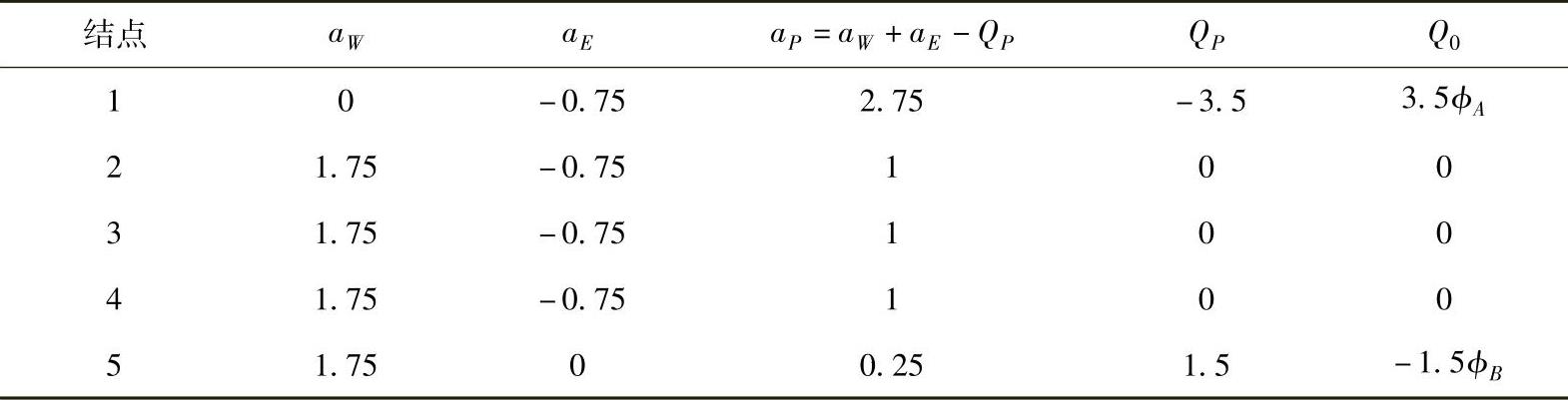
表4.5.1列出了离散方程的诸系数和等效源项计算公式。

表4.5.1 离散方程系数

978-7-111-44528-9-Chapter04-170.jpg

（1）第一种工况

u=0.1m/s，F=ρu=0.1，D=Γ/δx=0.1/0.2=0.5，代入表4.5.1可得表4.5.2所列的离散方程系数。

表4.5.2 离散方程系数

978-7-111-44528-9-Chapter04-171.jpg

将ϕA=1，ϕB=0代入，并将方程写成矩阵形式

978-7-111-44528-9-Chapter04-172.jpg

解此方程可得

978-7-111-44528-9-Chapter04-173.jpg

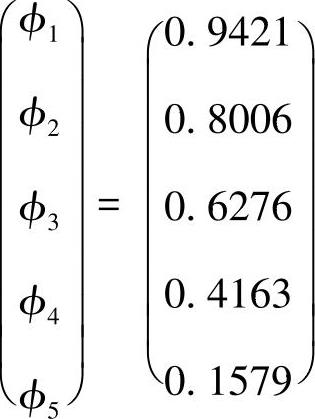
将已知数据代入解析解表达式（4.5.8）中，可得

978-7-111-44528-9-Chapter04-174.jpg

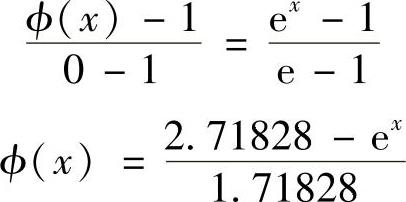
解析解和数值解的结果比较列于表4.5.3。

表4.5.3 解析解与有限体积法数值解对比

978-7-111-44528-9-Chapter04-175.jpg

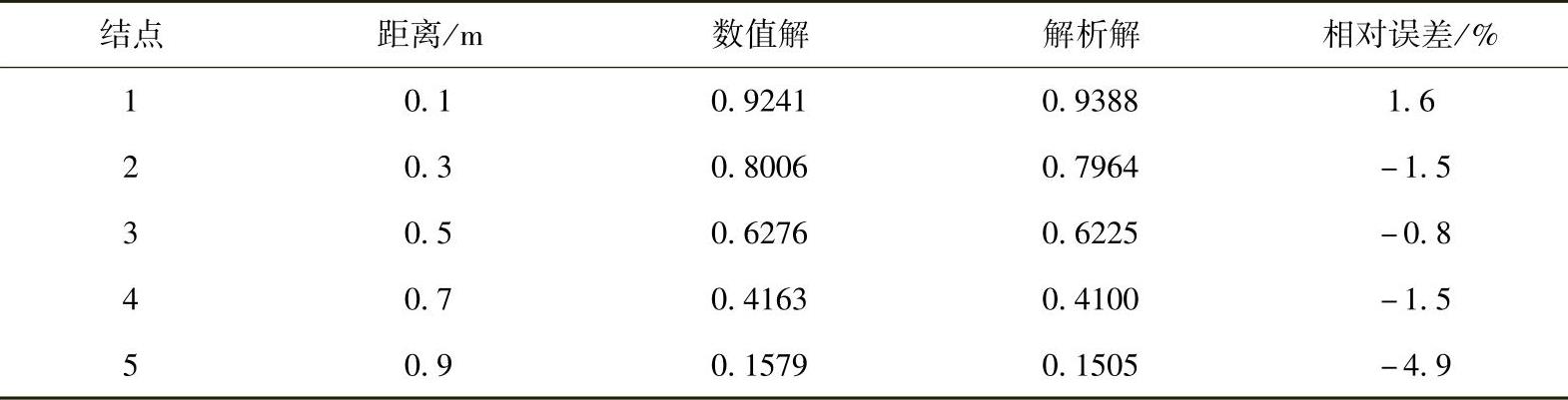
数值计算结果接近精确解，尽管计算网格比较粗糙，但仍得到合理结果。

（2）第二种工况

u=2.5m/s，F=ρu=2.5，D=Γ/δx=0.1/0.2=0.5，仍采用5个相等距离排列的结点网格系统，可得表4.5.4所列各系数。

表4.5.4 离散方程系数

978-7-111-44528-9-Chapter04-176.jpg

于是将ΦA=1，ΦB=0代入，有

978-7-111-44528-9-Chapter04-177.jpg

解此方程，得

978-7-111-44528-9-Chapter04-178.jpg

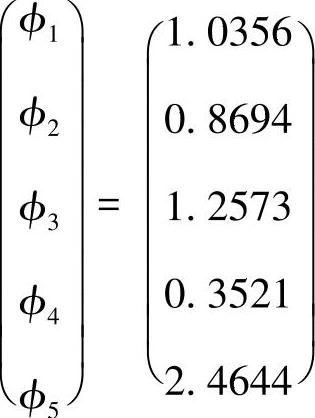
将已知数据代入解析解表达式（4.5.8）中，可得

978-7-111-44528-9-Chapter04-179.jpg

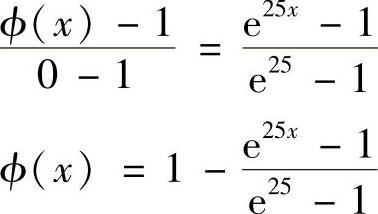
解析解和数值解的结果比较列于表4.5.5。

表4.5.5 解析解与有限体积法数值解对比

978-7-111-44528-9-Chapter04-180.jpg

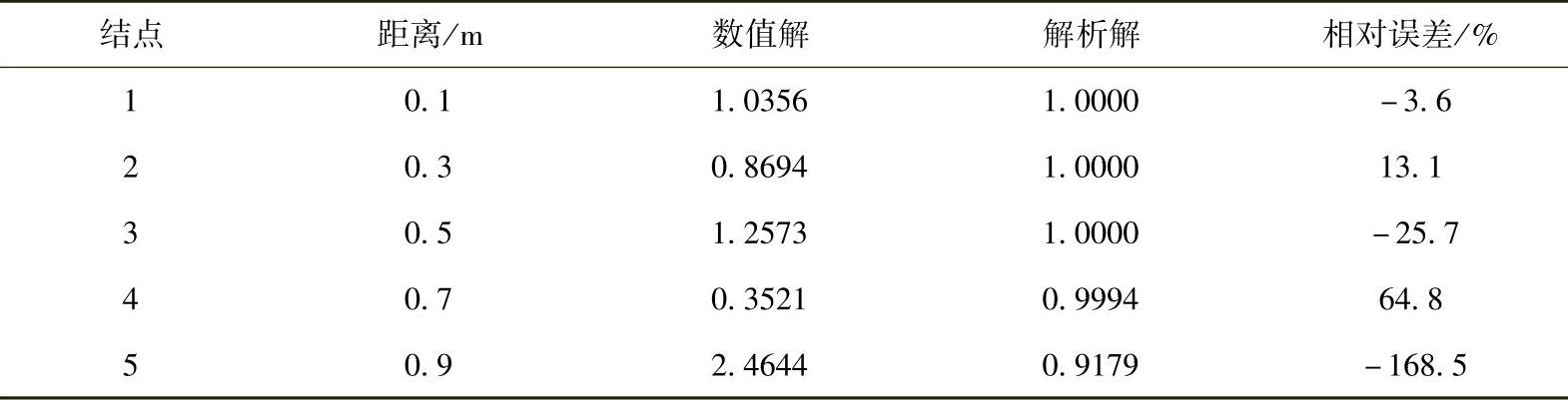
可以看出，数值解是在精确解周围振荡的。从表4.5.5中的误差可知，而这种计算精度是不可接受的，因此，必须采取措施提高数值解的计算精度，最直接的方法就是加密计算网格。

（3）第三种工况

计算区域取20个结点，此时δx=0.05，F=ρu=2.5，D=Γ/δx=0.1/0.05=2，由同样方法可得离散方程各系数，由表4.5.6给出。

表4.5.6 离散方程系数

978-7-111-44528-9-Chapter04-181.jpg

数值解与分析解的计算结果示于图4.5.4中，从图中可看出两者吻合得良好。网格数由5个加密到20，使得F/D从5减小到1.25。可见，网格加密可有效地改善数值解的计算精度。

978-7-111-44528-9-Chapter04-182.jpg

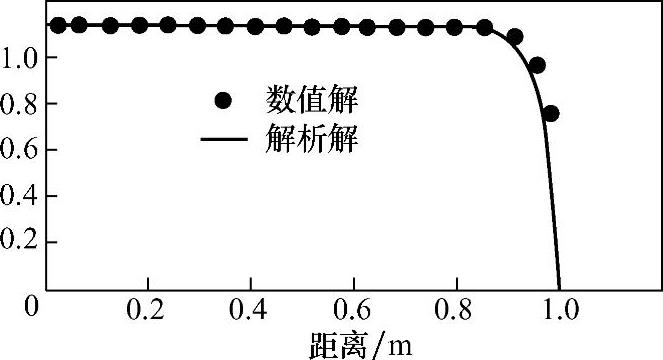
图4.5.4 解析解与数值解对比网格划分

免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。

我要反馈

有关偏微分方程数值解法：土建类的文章