【摘要】:三维稳态扩散问题满足下述控制方程这时应采用三维网格离散求解域,典型的控制容积如图4.4.4所示。综上所述,稳态扩散问题的有限体积法离散方程,对于一维、二维和三维扩散问题可写成统一的形式,即aPP=∑anbnb+Q0上式是关于一般结点P的离散方程通用表达式。

三维稳态扩散问题满足下述控制方程
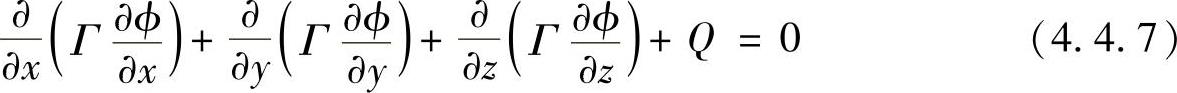
这时应采用三维网格离散求解域,典型的控制容积如图4.4.4所示。
结点P有6个相邻结点,分别位于东、西、南、北、上、下。与一维和二维问题类似,以e,w,s,n,t,b分别代表控制容积的东侧、西侧、南侧、北侧、上侧和下侧边界表面。
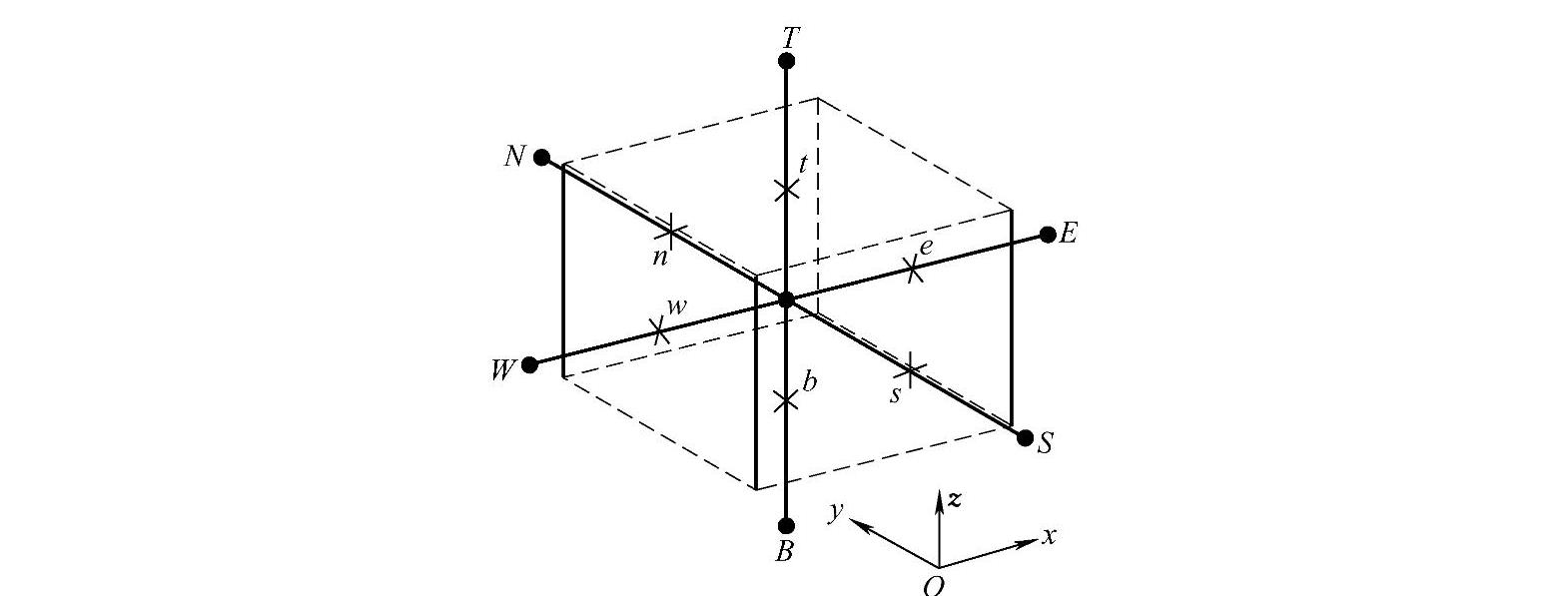
图4.4.4 三维控制容积及其相邻结点
在控制容 积内对方程式(4.4.7)积分,有
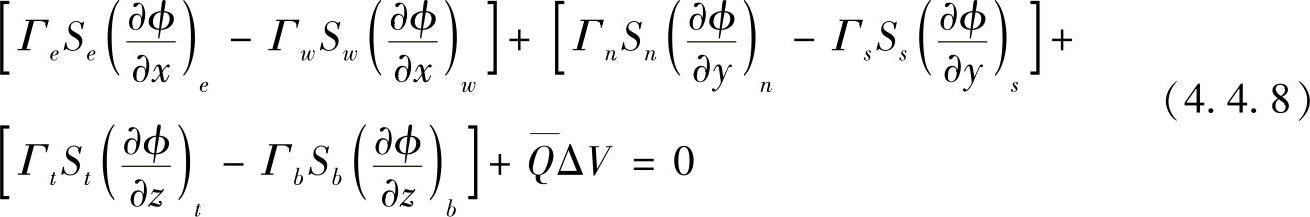
与一维、二维扩散问题推导过程一样,式(4.4.7)可近似写为
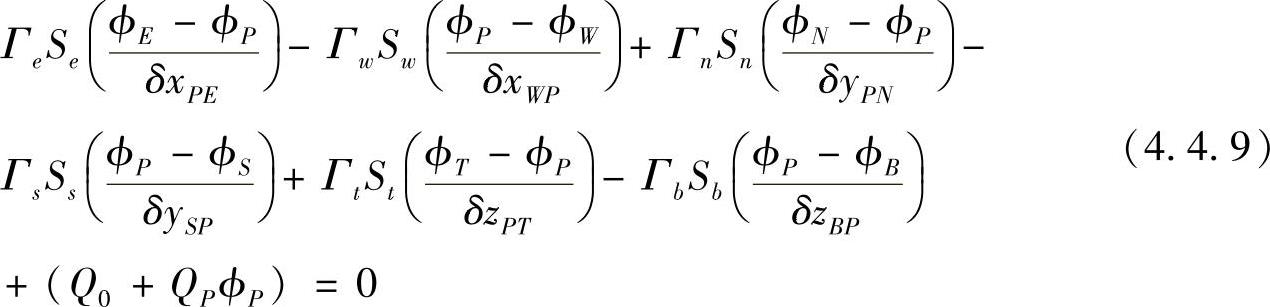
按结点场变量值整理方程式(4.4.9)可得(www.daowen.com)
aPϕP=aWϕW+aEϕE+aSϕS+aNϕN+aBϕB+aTϕT+Q0 (4.4.10)
式中,
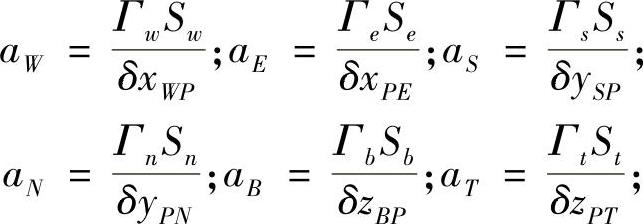
aP=aW+aE+aS+aN+aB+aT -QP
边界条件的引入与前文的处理方法相同,这里不再赘述。
综上所述,稳态扩散问题的有限体积法离散方程,对于一维、二维和三维扩散问题可写成统一的形式,即
aPϕP=∑anbϕnb+Q0
上式是关于一般结点P的离散方程通用表达式。式中的求和号表示所有与点P相邻结点(nb)上对应参数之和。anb表示相邻结点系数,对于一维问题anb为aW,aE;对二维问题anb为aW,aE,aS,aN;对于三维问题anb为aW,aE,aS,aN,aT,aB。ϕnb是场变量ϕ在点P相邻结点上的值。结点P的离散方程系数aP满足
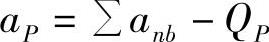
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
有关偏微分方程数值解法:土建类的文章







