› 理论教育 ›二维稳态扩散问题的有限体积法

二维稳态扩散问题的有限体积法

时间：2023-10-26 理论教育 版权反馈
【摘要】：由一维稳态扩散问题的有限体积法不难推广到二维扩散问题。二维稳态扩散问题的控制微分方程为式中，表示任意场变量；Γ为扩散系数。图4.4.1 二维网格第一步：生成离散网格图4.4.1为二维问题的离散网格的一部分，图中阴影区域为结点P的控制容积。方程式表示了场变量在控制容积内的平衡关系，即由扩散流入和流出的量与由源项产生的量之和为零。

二维稳态扩散问题的有限体积法

由一维稳态扩散问题的有限体积法不难推广到二维扩散问题。二维稳态扩散问题的控制微分方程为

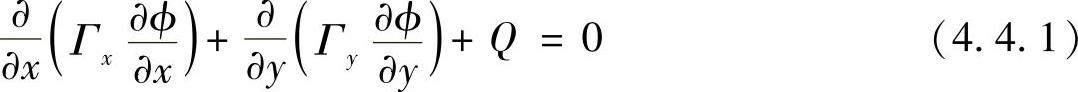
978-7-111-44528-9-Chapter04-109.jpg

式中，ϕ表示任意场变量；Γ为扩散系数。Γx与Γy可以不同或相同。为简便计算，我们假设Γx=Γy=Γ，Q为源项，仍分三步求解。

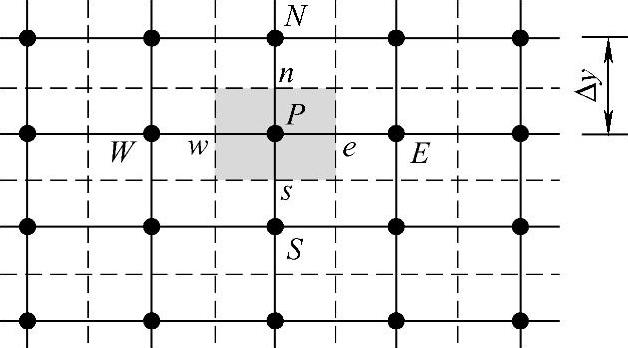
978-7-111-44528-9-Chapter04-110.jpg

图4.4.1 二维网格

第一步：生成离散网格

图4.4.1为二维问题的离散网格的一部分，图中阴影区域为结点P的控制容积。Δx可以不等于Δy。与一维问题不同，结点P除了有西侧相邻点W和东侧相邻点E外，还有北侧相邻点N和南侧相邻点S。结点P到W的x向距离仍记为δxWP，结点P到E的x向距离仍记为δxPE，另外还增加了南北向两个相邻点距离，分别记为δySP和δyPN。w，e，n，s分别取在点WP，PE，NP和PS的中心。

第二步：构造离散方程

按照有限体积法的基本思想，在控制容积中对式（4.4.1）积分，得

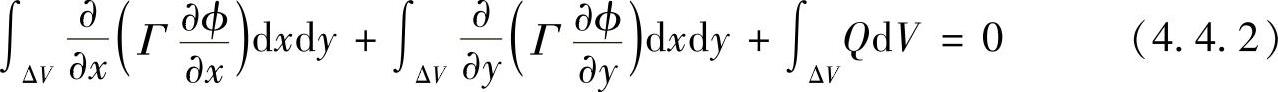
978-7-111-44528-9-Chapter04-111.jpg

由高斯公式可得

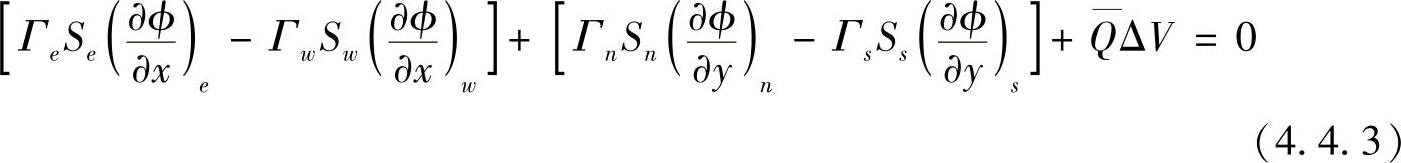
978-7-111-44528-9-Chapter04-112.jpg

从图4.4.1可知Se=Sw=Δy，Sn=Ss=Δx。方程式（4.4.33）表示了场变量ϕ在控制容积内的平衡关系，即由扩散流入和流出的量与由源项产生的量之和为零。

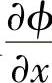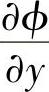为了计算式（4.4.3）中的各项，需要知道控制容积的东、西、南、北侧边界处的扩散率以及978-7-111-44528-9-Chapter04-113.jpg和978-7-111-44528-9-Chapter04-114.jpg，这里我们仍近似采用相邻结点处场变量值和扩散率值的线性插值，即

978-7-111-44528-9-Chapter04-115.jpg

代入式（4.4.3），得

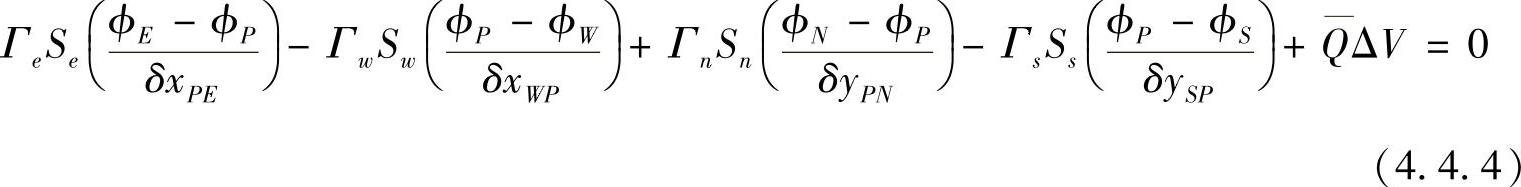
978-7-111-44528-9-Chapter04-116.jpg

将源项线性化处理，即QΔV=Q0+QPϕP，代入式（4.4.4）并按结点场变量整理，有

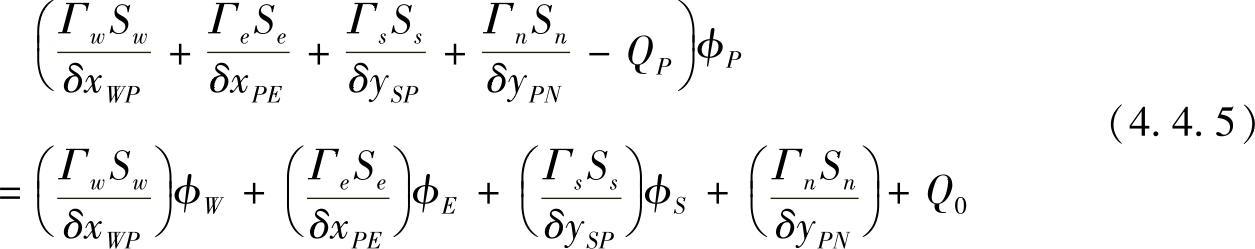
978-7-111-44528-9-Chapter04-117.jpg

各项系数用aP，aW，aE，aS，aN代替进行归一化处理，可将方程式（4.4.5）写成简洁的通用形式

aPϕP=aWϕW+aEϕE+aSϕS+aNϕN+Q0 （4.4.6）

式中，

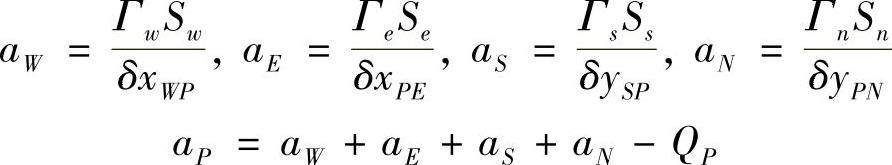
978-7-111-44528-9-Chapter04-118.jpg

式（4.4.6）适用于求解域中所有内部结点的离散方程构建。

第三步：解方程组

二维稳态扩散问题的有限体积法离散方程也是一组代数方程，其求解的办法同前。

【例4.4.1】如图4.4.2所示为二维纯铜板。板厚0.01m，导热系数λ=400W/（m·K），西侧边界有稳定热流输入，热流密度q=500kW/m2，东侧和南侧边界绝热，北侧边界保持常值温度，TN=100℃，求板内温度分布。

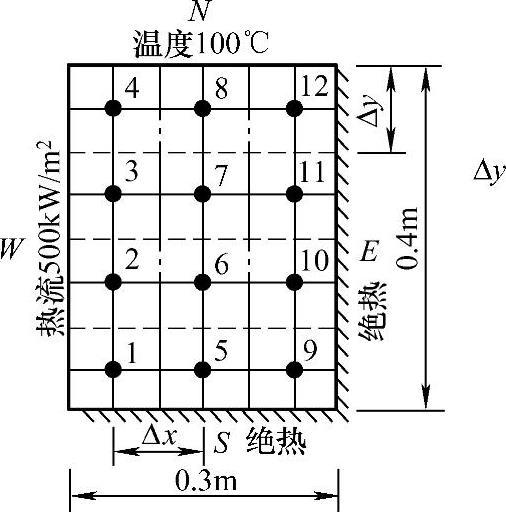
978-7-111-44528-9-Chapter04-119.jpg

图4.4.2 二维稳态问题及网格划分

【解】取均匀网格如图4.4.2所示，Δx=Δy=0.1m，二维无热源导热问题满足的控制微分方程为

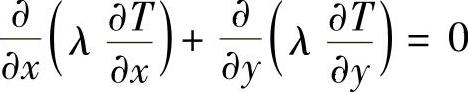
978-7-111-44528-9-Chapter04-120.jpg

由式（4.4.6），平板内结点所满足的离散方程有如下形式

aPϕP=aWϕW+aEϕE+aSϕS+aNϕN

式中，

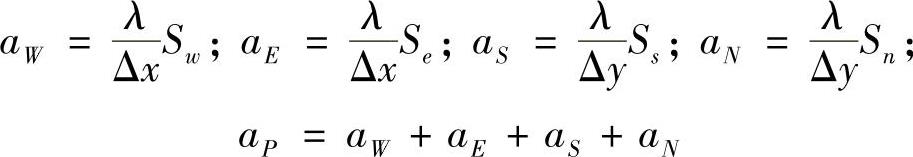
978-7-111-44528-9-Chapter04-121.jpg

由于网格均匀，Aw=Ae=As=An，Δx=Δy，λ为常数，有

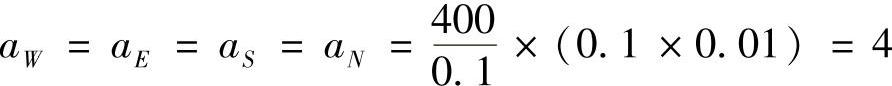
978-7-111-44528-9-Chapter04-122.jpg

图4.4.2 网格系统中，结点6，7为内结点，有

aP=aW+aE+aS+aN=4+4+4+4=16

结点6的离散方程为

16T6=4T2+4T10+4T5+4T7

结点7的离散方程为

16T7=4T3+4T11+4T6+4T8

除结点6和结点7以外的结点都是边界结点，边界点的离散方程形式为

aPϕP=aWϕW+aEϕE+aSϕS+aNϕN+Q0aP=aW+aE+aS+aN-QP

将边界条件引入方程式，求出等效源项Q0和QP。前面的例题中我们已得出均匀网格固定温度边界条件下的等效源项，即

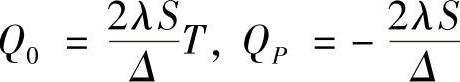
978-7-111-44528-9-Chapter04-123.jpg

式中，S为控制容积的边界面的面积；Δ为垂直于控制容积边界面的控制容积长度。

下面推导固定热流边界条件（对于绝热条件，q=0）的Q0和QP。由无热源一维导热方程

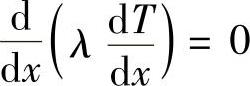
978-7-111-44528-9-Chapter04-124.jpg

在控制容积内积分

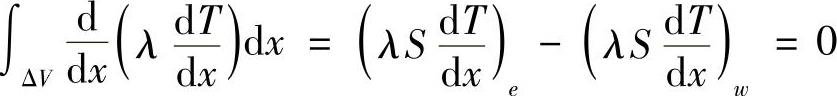
978-7-111-44528-9-Chapter04-125.jpg

上式表示进出控制容积东西侧界面的热扩散流量平衡。(www.daowen.com)

参看图4.4.3，在东侧界面由线性近似可写出

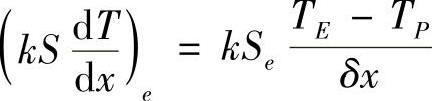
978-7-111-44528-9-Chapter04-126.jpg

而西侧界面，按照边界条件应有

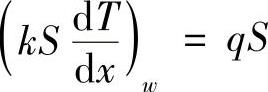
978-7-111-44528-9-Chapter04-127.jpg

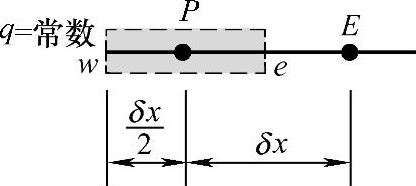
978-7-111-44528-9-Chapter04-128.jpg

图4.4.3 固定热流边界

即热流密度q乘以面积等于热流，即为通过该边界面导入或导出的热量。按热流密度定义，流出为正，流入为负，可得平衡方程为

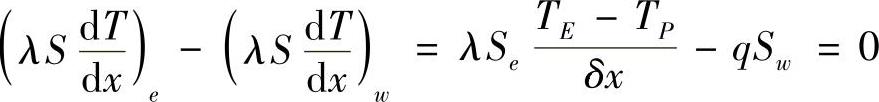
978-7-111-44528-9-Chapter04-129.jpg

按结点温度整理，有

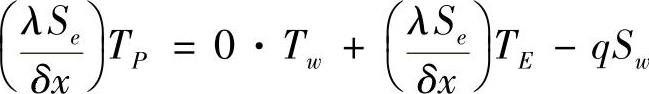
978-7-111-44528-9-Chapter04-130.jpg

这样我们就得到了固定热流密度边界结点离散方程的系数表达式为

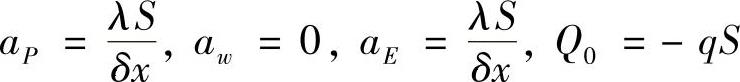
978-7-111-44528-9-Chapter04-131.jpg

总结起来，固定温度和固定热流边界条件的方程系数与源项列于表4.4.1中。

表4.4.1 固定温度和固定热流密度边界源项线性化系数

978-7-111-44528-9-Chapter04-132.jpg

利用表4.4.1，可求出个边界点的离散方程。

结点1：西侧边界为固定热流强度边界，有

aw=0

（Q0）w=qQw=500×1000×（0.1×0.01）=500

（QP）w=0

南侧边界为绝热边界，有

aS=0

（Q0）s=0

（QP）s=0

则总源项为

Q0=（Q0）w+（Q0）s=500

QP=（QP）w+（QP）s=0

结点1的离散方程为

aP=aW+aE+aS+aN -QP=0+4+0+4-0=8

8T1=4T2+4T5+500

结点4：西侧边界为固定热流强度边界，有

aw=0

（Q0）w=qSw=500×1000×（0.1×0.01）=500

（QP）w=0

北侧边界为固定温度边界，有

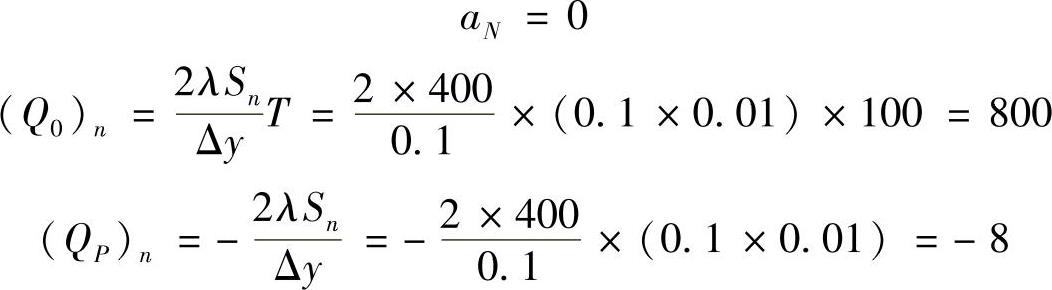
978-7-111-44528-9-Chapter04-133.jpg

总源项为

Q0=（Q0）w+（Q0）n=500+800=1300

QP=（QP）w+（QP）n=0-8=-8

于是，得结点4的离散方程为

aP=aW+aE+aS+aN -QP=0+4+0+4-（-8）=16

16T4=4T3+4T8+1300

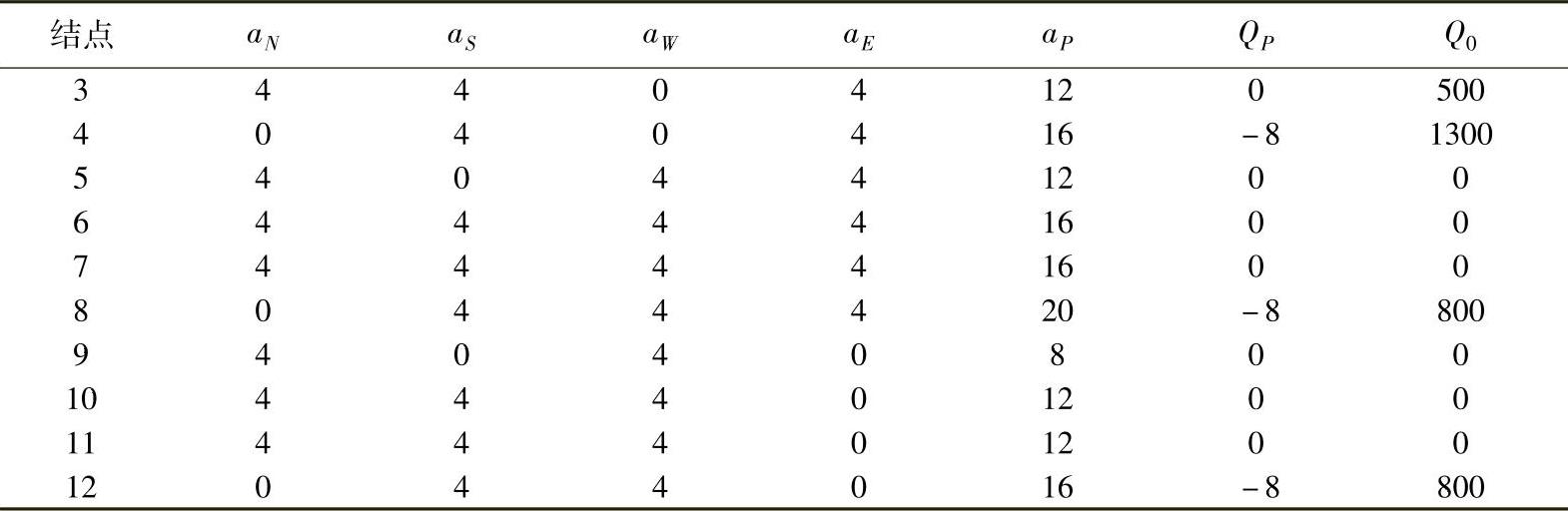
同样方法可求出结点2，3，5，8，9，10，11和结点12的离散方程，所有结点的离散方程系数与源项数值列于表4.4.2。

表4.4.2 离散方程系数

978-7-111-44528-9-Chapter04-134.jpg

（续）

978-7-111-44528-9-Chapter04-135.jpg

将方程写成矩阵形式，有

978-7-111-44528-9-Chapter04-136.jpg

解此方程组，得各结点的温度值，见表4.4.3。

表4.4.3 方程组数值解

978-7-111-44528-9-Chapter04-137.jpg

免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。

我要反馈

有关偏微分方程数值解法：土建类的文章