› 理论教育 ›一维稳态扩散问题的有限体积法:土建类数值解法

一维稳态扩散问题的有限体积法:土建类数值解法

时间：2023-10-26 理论教育 版权反馈
【摘要】：一维稳态扩散问题的控制微分方程为式中，表示任意场变量，如温度、速度；Γ为扩散系数；Q为源项。方程式有明确的物理意义，场变量流出右侧界面的扩散流量减去进入左侧界面的扩散流量等于的生成量，场变量在控制容积内达到平衡。用有限体积法求解下述无内热源一维稳态导热问题。

一维稳态扩散问题的有限体积法:土建类数值解法

一维稳态扩散问题的控制微分方程为

978-7-111-44528-9-Chapter04-57.jpg

式中，ϕ表示任意场变量，如温度、速度；Γ为扩散系数；Q为源项。

下面我们分三步来求解这一问题。

第一步：网格划分

与有限差分法相似，有限体积法首先将计算区域划分为一系列不重复的控制体，也就是将计算区域划分成等距或不等距的差分网格，并对每个网格结点周围划定一个控制容积，在每个控制体中设一个网格结点。如图4.3.1所示，将AB求解域划分成5个控制容积，区域边界即为控制容积的外边界，在每个控制容积的中心布置一个结点。

978-7-111-44528-9-Chapter04-58.jpg

图4.3.1 划分控制容积

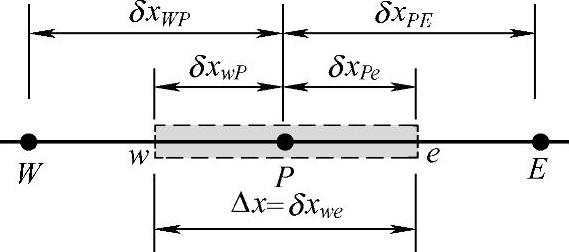
978-7-111-44528-9-Chapter04-59.jpg

图4.3.2 控制容积尺度定义

我们给出任意一个中间结点P所代表的控制容积尺度定义，如图4.3.2所示。点P的左侧相邻结点为W，右侧相邻结点为E，点W到点P的距离定义为δxWP，点P到点E的距离定义为δxPE，点P所在的控制容积左侧边界为w，右侧边界为e，控制容积长度为δxwe。

第二步：方程的离散

有限体积法是利用控制容积积分来实现方程的离散，在控制容积内对方程式（4.3.1）积分，并利用高斯公式，有

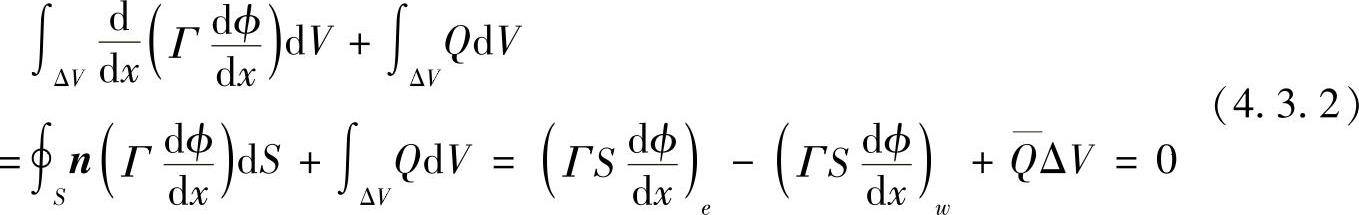
978-7-111-44528-9-Chapter04-60.jpg

式中，S为控制容积表面的面积；ΔV为控制容积的体积；Q为源项在控制容积的体积平均值。方程式（4.3.2）有明确的物理意义，场变量ϕ流出右侧界面的扩散流量减去进入左侧界面的扩散流量等于ϕ的生成量，场变量ϕ在控制容积内达到平衡。

要得到式（4.3.2）的具体形式，必须知道扩散系数Γ和场变量ϕ的梯度dϕ/dx在控制容积右侧（e）和左侧（w）边界上的值。这些值可利用结点上的相应值由插值运算求出，最简单的线性插值。例如，对均匀网格，有

978-7-111-44528-9-Chapter04-61.jpg

同理

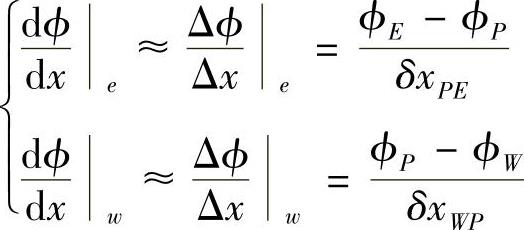
978-7-111-44528-9-Chapter04-62.jpg

对边界上的Γ值采用相邻两结点的Γ值的线性平均，类似于有限差分法的中心差分格式。经上面的处理，得到通过界面的扩散流量为

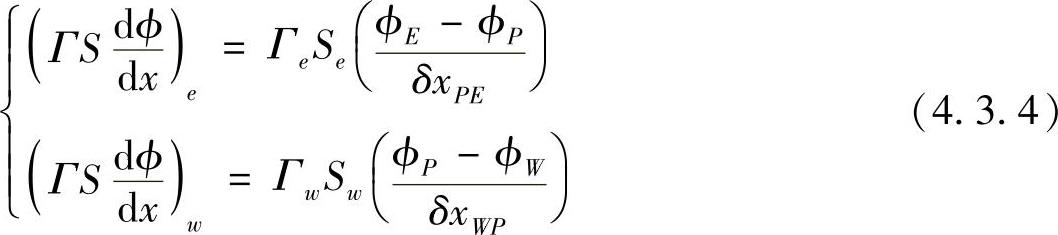
978-7-111-44528-9-Chapter04-63.jpg

源项可能是常数，也可能是场变量ϕ的函数，通常，有限体积法将源项作线性化处理，即设

978-7-111-44528-9-Chapter04-64.jpg

将式（4.3.3）～式（4.3.5）代入式（4.3.2），得

978-7-111-44528-9-Chapter04-65.jpg

按场变量ϕ的结点值整理方程式（4.3.6），得

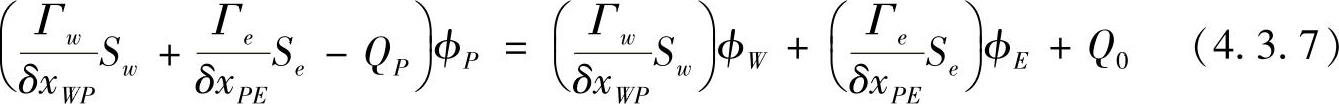
978-7-111-44528-9-Chapter04-66.jpg

将式（4.3.7）中各结点场变量系数归一化处理，写成aP，aW，aE，方程式（4.3.7）成为

aPϕP=aWϕW+aEϕE+Q0 （4.3.8）

式中，

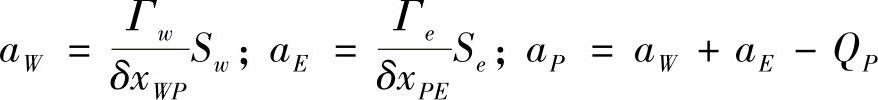
978-7-111-44528-9-Chapter04-67.jpg

方程式（4.3.8）即为一维稳态扩散方程式（4.3.1）的有限体积法离散方程，若对所有结点均列出对应的离散方程，最后将得到一组代数方程。对于求解域边界处的控制容积积分方程要按边界条件修正各系数。

第三步：解方程组

式（4.3.8）表示的方程组中每一个方程式相当于三元一次方程，因此我们得到的是一组三对角代数方程，求解线性代数方程组，即可得到各结点处的场变量值ϕ。

用有限体积法建立离散方程的关键是利用高斯公式把体积分转化为控制容积边界界面上的面积分，并且对界面上的参数作近似处理，若对Γ和ϕ等参数的近似处理方法不同，则必然会产生不同的离散格式。下面分别对无内热源和有内热源两种情况进行讨论。

【例4.3.1】用有限体积法求解下述无内热源一维稳态导热问题。

图4.3.3所示绝热细棒长0.5m，截面积S=0.01m2，左端温度TA保持在100℃，右端温度TB保持在500℃。若细棒材料为纯铜，其导热系数λ=400W/（m·K）。求绝热细棒在稳定状态下的温度分布。

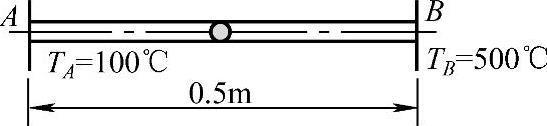
978-7-111-44528-9-Chapter04-68.jpg

图4.3.3 无内热源稳态导热

【解】无内热源一维稳态导热问题满足下述微分方程

978-7-111-44528-9-Chapter04-69.jpg

与式（4.3.1）相比，导热系数λ代替了扩散系数Γ，这里的场变量ϕ为温度T，源项Q=0。

第一步：生成离散网格

如图4.3.4所示，将棒划分成5个相等的控制容积，将结点置于控制容积的中心，共有5个结点，其中结点2，3，4为内部结点，结点1和5为边界结点。控制容积尺寸为

δx=0.5m/5=0.1m

第二步：构造离散方程

978-7-111-44528-9-Chapter04-70.jpg

图4.3.4 网格划分

对于内部结点，由式（4.3.8）可得结点温度的离散方程为

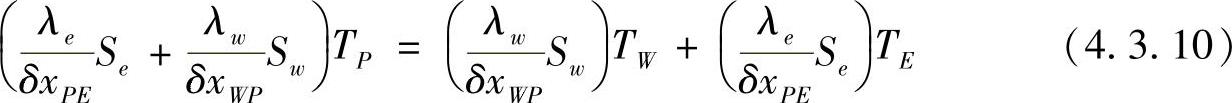
978-7-111-44528-9-Chapter04-71.jpg

由于λe=λw=λ，δxPE=δxWP=δx，Se=Sw=S均为常数，因此，对内部结点2、3和4有离散方程

aPTP=aWTW+aETE （4.3.11）

式中

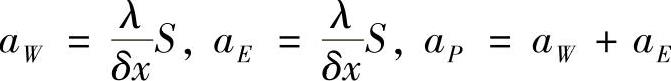
978-7-111-44528-9-Chapter04-72.jpg

因控制方程中无源项，Q0和QP均为零。

对于边界结点1和5，其离散方程需特殊处理，下面讨论边界点的离散方程。将式（4.3.9）在结点1的控制容积内进行积分，有

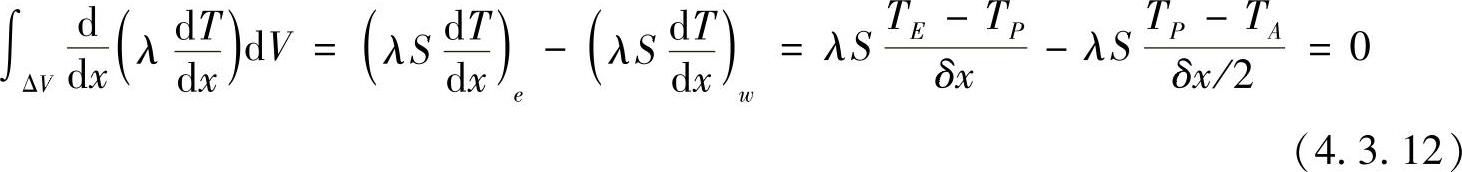
978-7-111-44528-9-Chapter04-73.jpg

这里的近似处理是通过控制容积的左侧界面的扩散流量近似与边界结点A和结点P的温度线性相关，按结点温度将方程式（4.3.12）整理，得

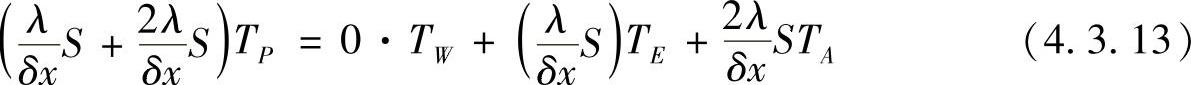
978-7-111-44528-9-Chapter04-74.jpg

将式（4.3.13）与式（4.3.8）比较可以看出，固定温度边界条件转化为源项（Q0+QPϕP）进入控制容积积分方程，其中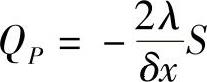，978-7-111-44528-9-Chapter04-75.jpg，978-7-111-44528-9-Chapter04-76.jpg。左侧边界点的温度系数为aW=0。从而边界结点1的离散方程可写为

aPTP=aWTW+aETE+Q0 （4.3.14）

式中，aW=0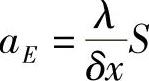；978-7-111-44528-9-Chapter04-77.jpg；aP=aW+aE-QP。

同理，将式（4.3.9）在结点5的控制容积内进行积分，有

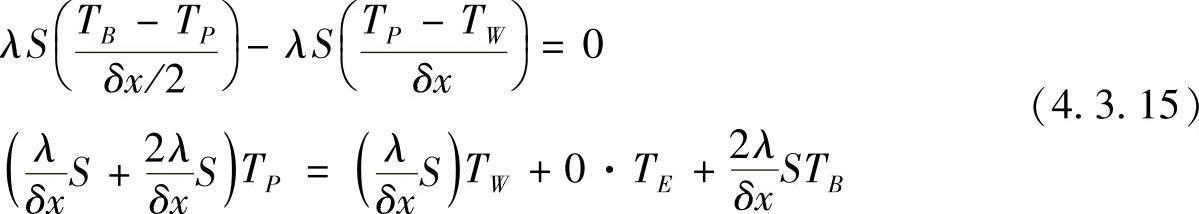978-7-111-44528-9-Chapter04-78.jpg(www.daowen.com)

从而边界点5的离散方程可写为

aPTP=aWTW+aETE+Q0 （4.3.16）

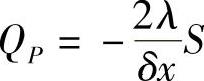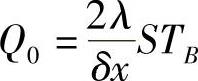式中，978-7-111-44528-9-Chapter04-79.jpg；aE=0；aP=aW+aE-QP；978-7-111-44528-9-Chapter04-80.jpg；978-7-111-44528-9-Chapter04-81.jpg。

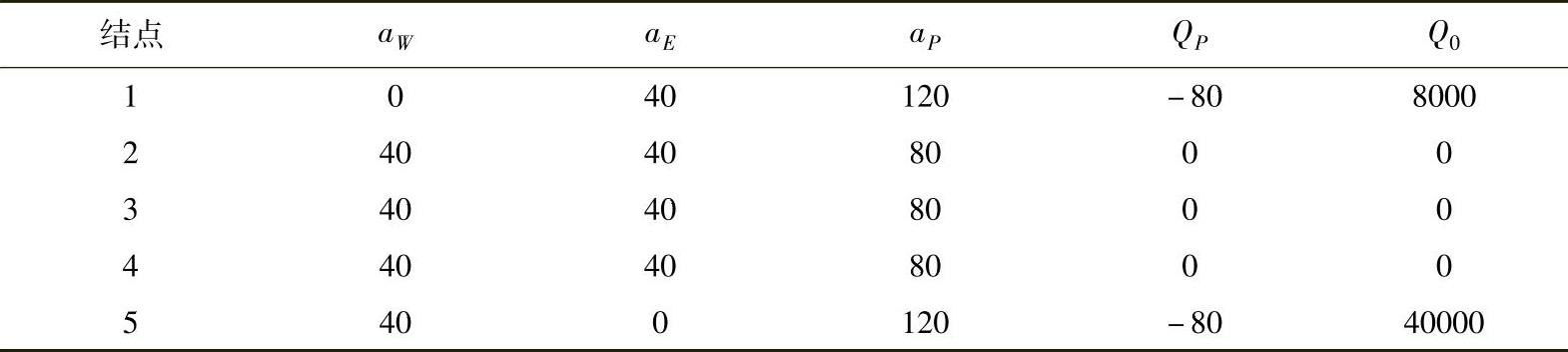
这样就得到了求解域内所有结点的离散方程，将已知数值代入式（4.3.11）、式（4.3.14）和式（4.3.16），λS/δx=400×0.01/0.1=40，各结点离散方程系数列于表4.3.1。

表4.3.1 离散方程系数

978-7-111-44528-9-Chapter04-82.jpg

从而可得下述代数方程组

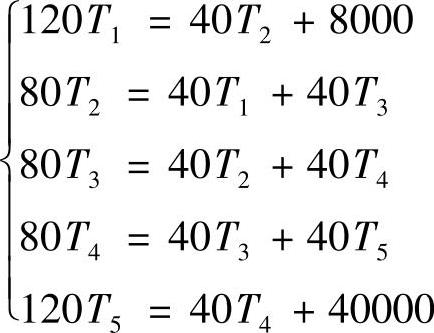
978-7-111-44528-9-Chapter04-83.jpg

写成矩阵形式，有

978-7-111-44528-9-Chapter04-84.jpg

第三步：解方程组

解此方程组，可得

978-7-111-44528-9-Chapter04-85.jpg

该问题的解析解为线性温度分布

T=800x+100

可以看出，数值解与解析解吻合良好，数值解有较高的计算精度。

978-7-111-44528-9-Chapter04-86.jpg

图4.3.5 含内热源无限大平板稳态导热

【例4.3.2】具有内热源的一维稳态导热问题。如图4.3.5所示，厚度为L=0.02m的无限大平板，导热系数λ=0.5W/（m·K），板内有均匀内热源Q=1.0×106W/m3，表面A温度保持为100℃，表面B温度保持为200℃。求板内x方向的温度分布。

【解】因平板在y，z方向为无限大，故可看做一维热传导问题。含内热源的一维热传导问题的控制方程为

978-7-111-44528-9-Chapter04-87.jpg

第一步：生成离散网格

将板厚度方向（x方向）分成5个控制容积，在每个控制容积的中心布置一个结点，如图4.3.6所示。此时δx=0.004m。在yOz平面考虑单位面积，即控制容积左、右侧边界面积S=1m2。

978-7-111-44528-9-Chapter04-88.jpg

图4.3.6 网格划分

第二步：构造离散方程

在控制容积内对方程式（4.3.17）积分，有

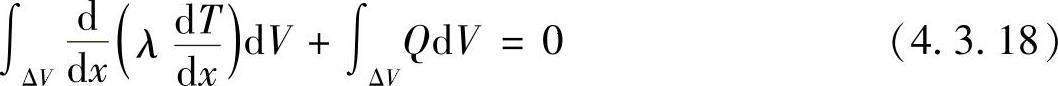
978-7-111-44528-9-Chapter04-89.jpg

第一项采用与例4.3.1相同的方法处理，第二项为源项，由于Q为常数，取QΔV=QΔV，从而式（4.3.18）成为

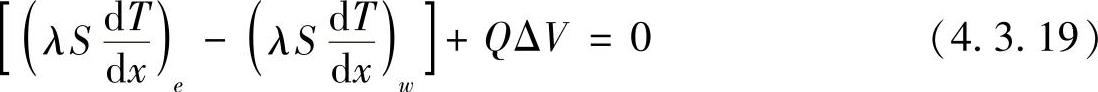
978-7-111-44528-9-Chapter04-90.jpg

对于一维问题，ΔV=Sδx

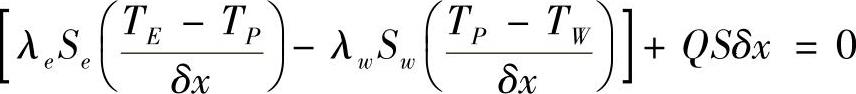
978-7-111-44528-9-Chapter04-91.jpg

按结点温度整理上式，得

978-7-111-44528-9-Chapter04-92.jpg

由于λe=λw=λ，Se=Sw=S，上式可写成通用形式

aPTP=aWTW+aETE+Q0 （4.3.21）

式中，978-7-111-44528-9-Chapter04-93.jpg；978-7-111-44528-9-Chapter04-94.jpg；aP=aW+aE-QP；QP=0；Q0=QSδx。

式（4.3.21）只适用于内结点2、3和4，边界点1和5需特殊处理。我们仍采用线性近似的方法，即区域边界处温度到相邻结点温度近似按线性变化。在结点1的控制容积内对式（4.3.17）积分，有

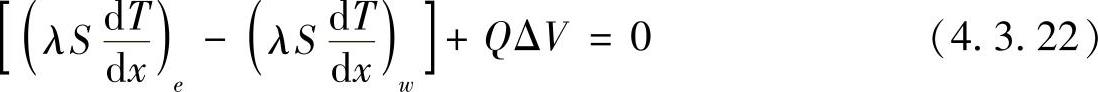
978-7-111-44528-9-Chapter04-95.jpg

在边界边A和结点P（此时为结点1）处引入线性温度近似，有

978-7-111-44528-9-Chapter04-96.jpg

按结点温度整理上式，可得边界结点1所在控制容积积分方程为

aPTP=aWTW+aETE+Q0 （4.3.24）

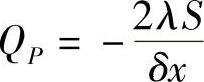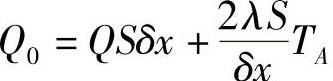式中，aW=0；978-7-111-44528-9-Chapter04-97.jpg；aP=aW+aE-QP；978-7-111-44528-9-Chapter04-98.jpg；978-7-111-44528-9-Chapter04-99.jpg。

对于结点5，控制容积右侧界面为区域边界，温度为已知值。类似于结点1的控制容积积分，有

978-7-111-44528-9-Chapter04-100.jpg

对上式按结点温度整理，得到边界结点5所在控制容积离散方程为

aPTP=aWTW+aETE+Q0 （4.3.26）

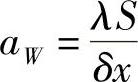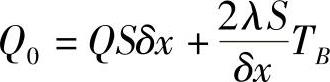式中，978-7-111-44528-9-Chapter04-101.jpg；aE=0；aP=aW+aE-QP；978-7-111-44528-9-Chapter04-102.jpg；978-7-111-44528-9-Chapter04-103.jpg。

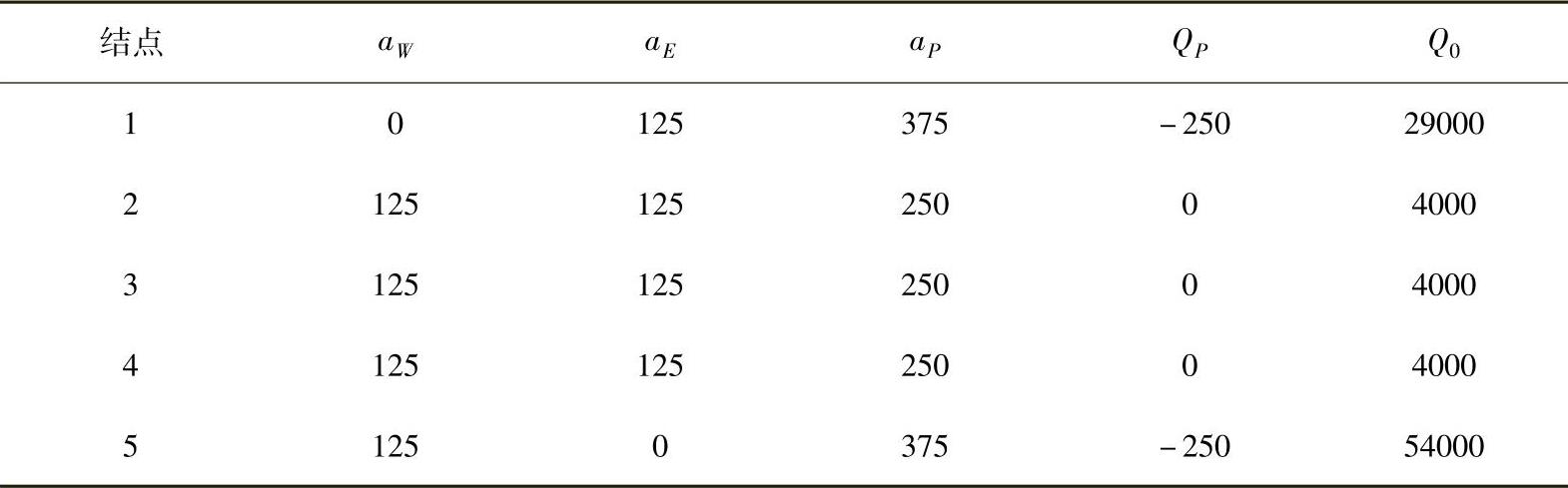
将A=1m2，λ=0.5W/（m·K），Q=1.0×106W/m3代入方程式（4.3.21）、式（4.3.24）和式（4.3.26），可得离散方程各系数，如表4.3.2所示。

表4.3.2 离散方程系数

978-7-111-44528-9-Chapter04-104.jpg

写成矩阵形式，有

978-7-111-44528-9-Chapter04-105.jpg

第三步：解方程组

解此方程组，可得

978-7-111-44528-9-Chapter04-106.jpg

方程式（4.3.17）的解析解为

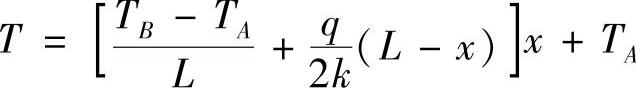
978-7-111-44528-9-Chapter04-107.jpg

有限体积法数值解与解析解在结点处的计算值及其误差列于表4.3.3。

表4.3.3 有限体积法数值解与解析解在结点处的计算值及其误差

978-7-111-44528-9-Chapter04-108.jpg

免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。

我要反馈

有关偏微分方程数值解法：土建类的文章