多维对流扩散方程，可简写为

式中，α为扩散系数；Q为源项。方程式（3.12.15）等式两端的四项依次是非稳定项、对流项、扩散项和源项，显然对流扩散方程是非线性偏微分方程。

如前文所述，为了获得稳定格式，需要把对流扩散方程中的时间导数用空间导数来代替，将对流扩散方程中的非稳定项进行泰勒级数展开

此时出现了因变量对时间的各阶导数。把式（3.12.15）写成下列形式

并将高阶时间导数转化为空间导数，与式（3.12.5）和式（3.12.6）类似取

于是有

忽略式（3.12.20）中右端三阶以上的导数项，并考虑到左端有下列关系

得到

取单元近似函数为

ψ=N_Jψ_J（t） （3.12.22）

式中，N_J为单元形函数；ψ_J（t）为t时刻结点J的因变量值，J=1，2，…，m；m为单元结点个数。(www.daowen.com)

于是得出式（3.12.21）的伽辽金弱解形式为

将ψ=N_Jψ_J（t）和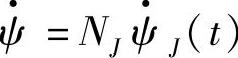代入式（3.12.23），得到单元的有限元方程为

其中，

对式（3.12.25）～式（3.12.28）施行分部积分并利用GreenGauss公式，可以进一步得到

至此，完成了有限元的单元分析。将计算域中所有单元的有限元方程叠加在一起，就构成总体有限元方程

式中，A=᥂A_IJ；B=᥂B_IJ；F=᥂F_I。式（3.12.32）即为多维对流扩散方程的泰勒伽辽金有限元列式。

常规伽辽金有限元法无法引入迎风效应，泰勒伽辽金有限元法可自然地引入迎风效应。为了回答泰勒伽辽金有限元法如何实现迎风格式的问题，只需将标准对流扩散方程的常规伽辽金有限元离散格式与泰勒伽辽金有限元离散格式进行对比。为此，仍取单元近似函数为式（3.12.22），式中符号意义同前。采用常规伽辽金有限元法离散化处理式（3.12.15），得单元有限元方程为

其中，

将式（3.12.24）与式（3.12.33）相减得

根据泰勒伽辽金有限元法得到的单元离散方程比常规伽辽金有限元法要复杂，这是由于对时间导数进行泰勒级数展开，并将其中对时间的二阶和三阶导数转化为空间导数产生的。式（3.12.37）与式（3.12.38）的右端项，在形式上是一个对空间二阶导数的有限元离散格式，并不是人为加入的，而是通过时间导数和空间导数的相互转换直接得到的。因此，可以得出，时间与空间离散是相互关联的，更高阶的耗散机理不仅可以采用空间迎风格式获得，也可以通过高阶时间导数的离散实现。此外，通过对式（3.12.24）进行稳定性分析，还可以看到，该泰勒伽辽金有限元格式保留了三阶离散精度。