下面以一阶双曲型方程为例，简要介绍泰勒伽辽金有限元法。对于一维对流方程

u_t=au_x （3.12.1）

式中，a是非负常数。采用时间前差格式，对时间项进行离散化处理

其中，Δt是时间增量，上标n表示时间增量步。

在有限差分法中已讨论过，对于式（3.12.3）右端的空间导数项，若采用中心差分格式，通过稳定性分析可知，这种格式恒不稳定，这是由于u_x的计算时刻n先于u_t的计算时刻n=1。若能在同一时刻计算u_x和u_t，则可形成稳定的格式。为此，最简单的办法就是用n时刻的参数来表示u_t的差分近似，显然，这可以由时间向前的泰勒级数展开去实现

对式（3.12.1）依次对时间求导，得

u_tt=a²u_xx （3.12.5）

u_ttt=a²（u_t）_xx （3.12.6）

将式（3.12.5）和式（3.12.6）代入式（3.12.4）得

比较式（3.12.3）和（3.12.7）可以发现，后者多出两项对x的二阶导数项，这两项不是人为加入的，而是对u_t高阶差分近似的一部分，是通过把泰勒级数展开中的高阶时间导数转化为空间导数而自然出现的。在式（3.12.7）中，用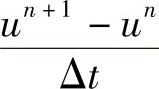代替u_t，得

采用伽辽金法离散化处理式（3.12.8），并取单元的近似函数为

得到式（3.12.8）的泰勒伽辽金有限元弱解形式(www.daowen.com)

从以上导出的一维对流方程泰勒伽辽金有限元弱解形式可以看出，泰勒伽辽金有限元法的基本思想是通过控制微分方程的一阶时间导数用时间向前的泰勒级数展开，使其中至少包括二阶以上的时间导数，从而提高对时间导数项的差分近似程度，再根据原控制方程将高阶时间导数转化为空间导数，便会自然地引入二阶导数项，获得稳定的计算格式。

在有限差分法中已讨论过，在分析离散格式的稳定性时通常把所分析的差分格式应用于一维稳态无源的模型方程，通过对这一差分方程稳定性的分析，来研究该格式下稳定性的条件，因为采用的控制方程简单，就可能找出差分格式产生对流不稳定性的某些原因。在有限元法中也是这样，稳定性分析的主要方法之一是Fourier分析法。

为了研究泰勒伽辽金有限元法的稳定性，以上述一维对流方程进行分析。如果取分段线性的单元基函数，网格尺寸为l，则式（3.12.10）可以化为以结点参数u_jⁿ表示的形式

其中，

假定u_jⁿ存在误差ε_jⁿ，u_jⁿ⁺¹存在误差ε_jⁿ⁺¹，代入式（3.12.11），可以推出

对误差ε_jⁿ⁺¹和ε_jⁿ作傅里叶展开，整理后可以得到

ε_jⁿ⁺¹=λ（p）e^iCpε_jⁿ （3.12.13）

其中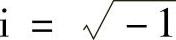，；λ（p）为增长因子；p=lK，K为波数。将式（3.12.13）代入式（3.12.12），可得

当p→0时，有

可以看出，当C_r≤1时，|λ（p）|≤1，因此，稳定性条件为C_r＜1。