考虑一维抛物型方程

其伽辽金积分表达式为

分部积分后得

其中，D为求解域，Γ₂是自然边界。

对上式中的时间导数项采用式（3.11.2）的插值函数，并取δu=N_i可以获得单元有限元方程为

其中

若e单元中没有边界落在自然边界Γ₂上，则f_i（e）取零值。

将单元有限元方程（3.11.5）在全域内汇集起来，可得到总体有限元方程

对（3.11.6）进行强加边界条件处理，如采用对角线项扩大法，只需对B_nm和f_n相应的元素乘以一个大数G。若第r结点属于强加边界条件，并有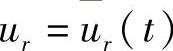，则元素Brr改为GB_rr，f_r改为Gf_ru_r，其余结点的处理类同，并可得到修正后的总体有限元方程

这是一个含有N个未知数u₁^（t），u₂^（t），…，u_N^（t）的常微分方程组，其初值条件为

u_i（t）|_t=0=u₀（x_i）=u_i^（0） （3.11.8）(www.daowen.com)

其中初值函数

u₀（x）=u（x，t）|_t=0

可由原始偏微分方程的初值条件给出。

微分方程组（3.11.7），一般采用有限差分解法，对求解的时间区间[0，T]进行离散化处理。设时间步长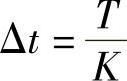，t=t_k=kΔt（k=1，2，…，K），时间导数项u·_m引进差分算子

将上列三种差分格式代入式（3.11.7）后也有相应的三种不同的形式。以向前差分格式为例，有

对于式（3.11.9）中的u_m，也可以采用不同的形式，如

根据上式，相应于式（3.11.9）有三种形式，并可统一写成如下形式

上式中的θ分别取1，0和1/2，就是u_m取式（3.11.10）中三种数值时，相应于式（3.11.9）的步进法有限元方程。由式（3.11.11）可以根据前时段各结点的值u_m（k），反复求得后时段各结点的值u_m（k+1）。

有限元方程式（3.11.11）中当θ=1时，等号左边括号内的第二项为零，这时式（3.11.11）是对求解u_m（k+1）的显式格式。当θ=0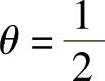，时，式（3.11.11）则为隐式格式。可以证明，上面的显式格式是属于有条件稳定的，而隐式格式则是无条件稳定的，使用时应当注意。